LeetCode刷题实战45:跳跃游戏 II
算法的重要性,我就不多说了吧,想去大厂,就必须要经过基础知识和业务逻辑面试+算法面试。所以,为了提高大家的算法能力,这个公众号后续每天带大家做一道算法题,题目就从LeetCode上面选 !
今天和大家聊的问题叫做 跳跃游戏 II,我们先来看题面:
https://leetcode-cn.com/problems/jump-game-ii/
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
题意
样例
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
说明:
假设你总是可以到达数组的最后一个位置。
解题

搜索
class Solution:
def jump(self, nums: List[int]) -> int:
import queue
n = len(nums)
que = queue.Queue()
que.put((0, 0))
while not que.empty():
pos, step = que.get()
if pos >= n-1:
return step
for i in range(pos, min(n, pos+nums[pos] + 1)):
que.put((i, step+1))
class Solution:
def jump(self, nums: List[int]) -> int:
import queue
n = len(nums)
que = queue.Queue()
que.put((0, 0))
visited = set()
while not que.empty():
pos, step = que.get()
if pos >= n-1:
return step
for i in range(pos, min(n, pos+nums[pos] + 1)):
# 如果已经入过队列了则跳过
if i in visited:
continue
que.put((i, step+1))
visited.add(i)
class Solution:
def jump(self, nums: List[int]) -> int:
import queue
n = len(nums)
que = queue.Queue()
que.put((0, 0))
visited = set()
while not que.empty():
pos, step = que.get()
if pos >= n-1:
return step
# 倒叙遍历
for i in range(min(n-1, pos+nums[pos]), pos, -1):
# 当遇到已经遍历过的元素的时候直接break
if i in visited:
break
que.put((i, step+1))
visited.add(i)
class Solution:
def jump(self, nums: List[int]) -> int:
import queue
n = len(nums)
# 使用优先队列
que = queue.PriorityQueue()
que.put((0, 0, 0))
visited = set()
while not que.empty():
_, pos, step = que.get()
if pos >= n-1:
return step
# 倒叙遍历
for i in range(min(n-1, pos+nums[pos]), pos, -1):
if i in visited:
break
# 由于优先队列是默认元素小的排在前面,所以加上负号
que.put((-i - nums[i] ,i, step+1))
visited.add(i)
贪心
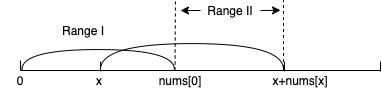
class Solution:
def jump(self, nums: List[int]) -> int:
n = len(nums)
start, end = 0, nums[0]
step = 1
if n == 1:
return 0
while end < n-1:
maxi, idx = 0, 0
# 维护下一个区间
for i in range(start, end+1):
if i + nums[i] > maxi:
maxi, idx = i + nums[i], i
# 下一个区间的起始范围
start, end = end+1, maxi
step += 1
return step
上期推文:
评论
