哈工大硕士生实现 11 种数据降维算法,代码已开源!
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
01 为什么要进行数据降维?

使得数据集更易使用
确保变量之间彼此独立
降低算法计算运算成本
去除噪音

02 数据降维原理

线性降维方法:
非线性降维方法:
03 主成分分析(PCA)降维算法
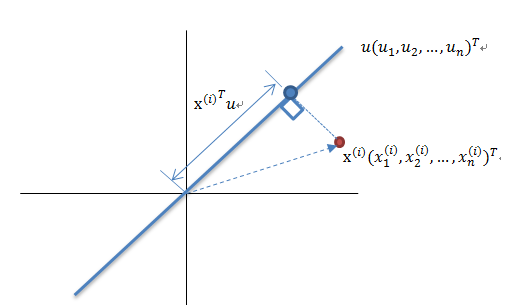
算法输入:数据集 Xmxn;
按列计算数据集 X 的均值 Xmean,然后令 Xnew=X−Xmean;
求解矩阵 Xnew 的协方差矩阵,并将其记为 Cov;
计算协方差矩阵 COv 的特征值和相应的特征向量;
将特征值按照从大到小的排序,选择其中最大的 k 个,然后将其对应的 k 个特征向量分别作为列向量组成特征向量矩阵 Wnxk;
计算 XnewW,即将数据集 Xnew 投影到选取的特征向量上,这样就得到了我们需要的已经降维的数据集 XnewW。
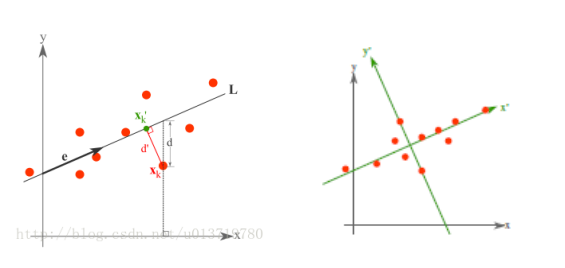
详细步骤可参考《从零开始实现主成分分析 (PCA) 算法》: https://blog.csdn.net/u013719780/article/details/78352262
04 主成分分析(PCA)代码实现
from __future__ import print_function
from sklearn import datasets
import matplotlib.pyplot as plt
import matplotlib.cm as cmx
import matplotlib.colors as colors
import numpy as np
%matplotlib inline
def shuffle_data(X, y, seed=None):
if seed:
np.random.seed(seed)
idx = np.arange(X.shape[0])
np.random.shuffle(idx)
return X[idx], y[idx]
# 正规化数据集 X
def normalize(X, axis=-1, p=2):
lp_norm = np.atleast_1d(np.linalg.norm(X, p, axis))
lp_norm[lp_norm == 0] = 1
return X / np.expand_dims(lp_norm, axis)
# 标准化数据集 X
def standardize(X):
X_std = np.zeros(X.shape)
mean = X.mean(axis=0)
std = X.std(axis=0)
# 做除法运算时请永远记住分母不能等于 0 的情形
# X_std = (X - X.mean(axis=0)) / X.std(axis=0)
for col in range(np.shape(X)[1]):
if std[col]:
X_std[:, col] = (X_std[:, col] - mean[col]) / std[col]
return X_std
# 划分数据集为训练集和测试集
def train_test_split(X, y, test_size=0.2, shuffle=True, seed=None):
if shuffle:
X, y = shuffle_data(X, y, seed)
n_train_samples = int(X.shape[0] * (1-test_size))
x_train, x_test = X[:n_train_samples], X[n_train_samples:]
y_train, y_test = y[:n_train_samples], y[n_train_samples:]
return x_train, x_test, y_train, y_test
# 计算矩阵 X 的协方差矩阵
def calculate_covariance_matrix(X, Y=np.empty((0,0))):
if not Y.any():
Y = X
n_samples = np.shape(X)[0]
covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0))
return np.array(covariance_matrix, dtype=float)
# 计算数据集 X 每列的方差
def calculate_variance(X):
n_samples = np.shape(X)[0]
variance = (1 / n_samples) * np.diag((X - X.mean(axis=0)).T.dot(X - X.mean(axis=0)))
return variance
# 计算数据集 X 每列的标准差
def calculate_std_dev(X):
std_dev = np.sqrt(calculate_variance(X))
return std_dev
# 计算相关系数矩阵
def calculate_correlation_matrix(X, Y=np.empty([0])):
# 先计算协方差矩阵
covariance_matrix = calculate_covariance_matrix(X, Y)
# 计算 X, Y 的标准差
std_dev_X = np.expand_dims(calculate_std_dev(X), 1)
std_dev_y = np.expand_dims(calculate_std_dev(Y), 1)
correlation_matrix = np.divide(covariance_matrix, std_dev_X.dot(std_dev_y.T))
return np.array(correlation_matrix, dtype=float)
class PCA():
"""
主成份分析算法 PCA,非监督学习算法.
"""
def __init__(self):
self.eigen_values = None
self.eigen_vectors = None
self.k = 2
def transform(self, X):
"""
将原始数据集 X 通过 PCA 进行降维
"""
covariance = calculate_covariance_matrix(X)
# 求解特征值和特征向量
self.eigen_values, self.eigen_vectors = np.linalg.eig(covariance)
# 将特征值从大到小进行排序,注意特征向量是按列排的,即 self.eigen_vectors 第 k 列是 self.eigen_values 中第 k 个特征值对应的特征向量
idx = self.eigen_values.argsort()[::-1]
eigenvalues = self.eigen_values[idx][:self.k]
eigenvectors = self.eigen_vectors[:, idx][:, :self.k]
# 将原始数据集 X 映射到低维空间
X_transformed = X.dot(eigenvectors)
return X_transformed
def main():
# Load the dataset
data = datasets.load_iris()
X = data.data
y = data.target
# 将数据集 X 映射到低维空间
X_trans = PCA().transform(X)
x1 = X_trans[:, 0]
x2 = X_trans[:, 1]
cmap = plt.get_cmap('viridis')
colors = [cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))]
class_distr = []
# Plot the different class distributions
for i, l in enumerate(np.unique(y)):
_x1 = x1[y == l]
_x2 = x2[y == l]
_y = y[y == l]
class_distr.append(plt.scatter(_x1, _x2, color=colors[i]))
# Add a legend
plt.legend(class_distr, y, loc=1)
# Axis labels
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()
if __name__ == "__main__":
main()
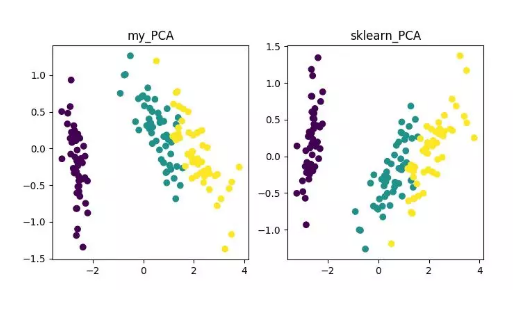
05 其它降维算法及代码地址
KPCA(kernel PCA)
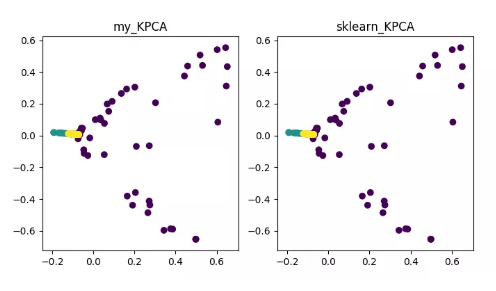
详细内容可参见 《Python 机器学习》之特征抽取——kPCA: https://blog.csdn.net/weixin_40604987/article/details/79632888 代码地址: https://github.com/heucoder/dimensionality_reduction_alo_codes/blob/master/codes/PCA/KPCA.py
LDA(Linear Discriminant Analysis)
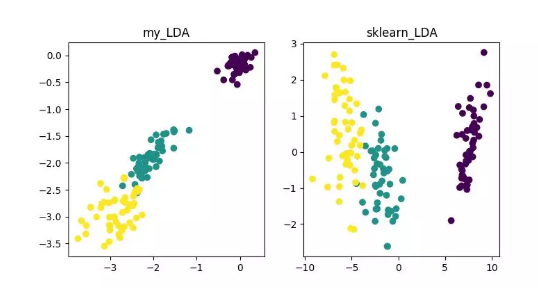
详细内容可参见《数据降维—线性判别分析(LDA)》: https://blog.csdn.net/ChenVast/article/details/79227945 代码地址: https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/LDA
MDS(multidimensional scaling)
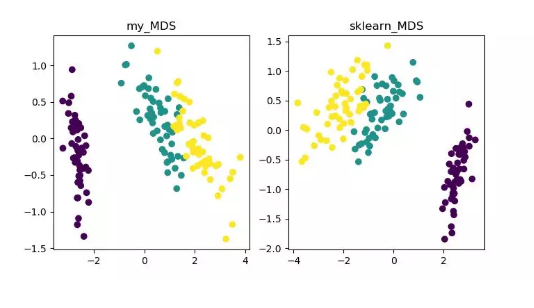
详细内容可参见《MDS 算法》 https://blog.csdn.net/zhangweiguo_717/article/details/69663452 代码地址: https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/MDS
ISOMAP
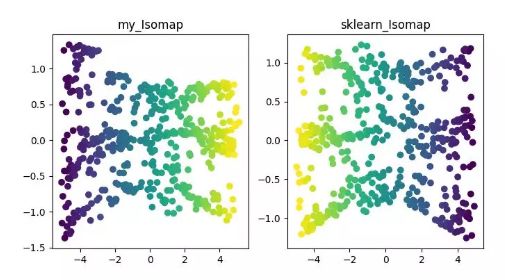
详细内容可参见《Isomap》 https://blog.csdn.net/zhangweiguo_717/article/details/69802312 代码地址: https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/ISOMAP
LLE(locally linear embedding)
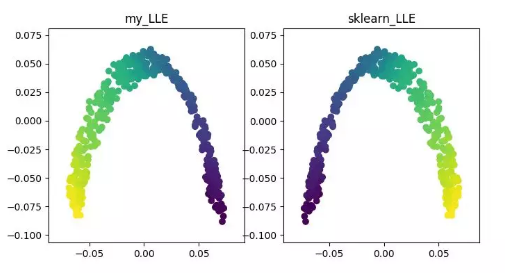
详细内容可参见《LLE 原理及推导过程》 https://blog.csdn.net/scott198510/article/details/76099630 代码地址: https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/LLE
t-SNE
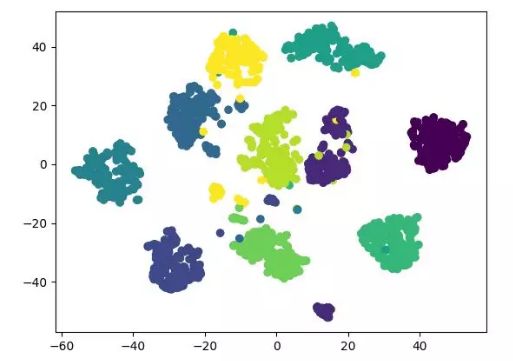
详细内容可参见《t-SNE 使用过程中的一些坑》: http://bindog.github.io/blog/2018/07/31/t-sne-tips/ 代码地址: https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/T-SNE
LE(Laplacian Eigenmaps)
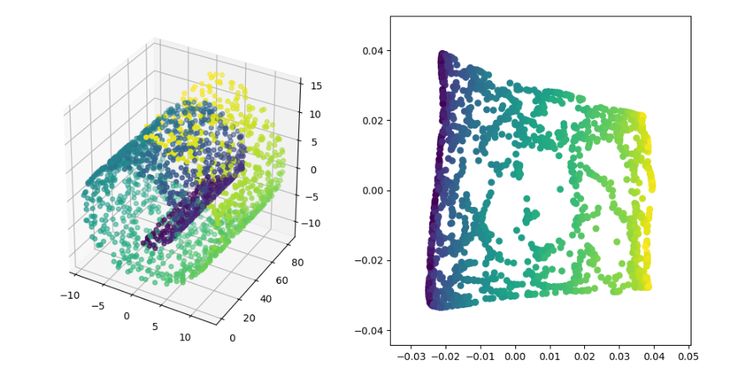
详细内容可参见《拉普拉斯特征图降维及其 python 实现》: https://blog.csdn.net/HUSTLX/article/details/50850342 代码地址: https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/LE
LPP(Locality Preserving Projections)
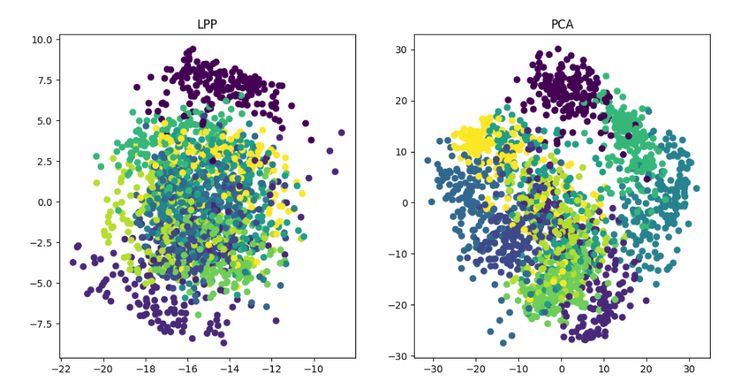
评论
