同济版《线性代数》引争议，从清华改用MIT数学课程看中美数学教育差距！-技术圈

不论是结构力学还是人脸识别，理工类型的科研，深究之后就会发现到处都是线性代数的身影。这样一门课程，要是在大一的时候学不好，可是会要命的。

在国内上过大学的理科同学应该都见过《线性代数》（同济版），就算没有学过，也是听过它的大名。作为一名过来人，只能说，晦涩难懂，章节混杂... 即使不少 985、211 走过高考独木桥的学生，每到期末考试，也要默默祈祷不要挂科。现在想起一些内容：相似矩阵、线性变换、特征值、特征向量…… 真是一个头两个大。

作为一本大学教材，让学习者如此后怕，是该考虑一下教材问题了。如今已经毕业多年，没想到最近在知乎上看到一篇文章《《线性代数》（同济版）——教科书中的耻辱柱》，点赞量快突破五千。对于这篇文章，大家有时间可以读一下，看看是不是同意作者的观点。

线性代数真的很重要，这是很多工程技术人员走上工作岗位的最大感受。好多算法都用到线性代数的知识，就比如现在非常热门的深度学习，它的底层实现方式用到好多线性代数方面的知识。如果底层基础打不好，不明白其中的原理，算法实现方式真的很难理解，更不可能去创新了。好的教材才能起到事半功倍的效果。

目前这本教材已更新了好几版，每次更新的内容看起来也是无关紧要，如果有下次版本更新，还是希望制定教材的老师们听取一下广大学生的建议。

同济版《线性代数》何以引发众怒？

一直以来，同济版《线性代数》都是一本颇有争议的教材，它在知乎上的风评基本都是这个画风：

很多同学吐槽这本教材结构不合理、内容抽象（甚至让抽象的东西变得更抽象），整本学下来很难有什么收获，还可能会丧失对于数学学习的兴趣。

以下是对于这些观点的简单总结：

1、结构编排不合理
很多发帖的同学都指出，同济版《线性代数》最大的问题就是「结构混乱」，第一章就从「行列式」开始讲。对于没有学过线性代数基本概念的大一同学来讲，这种毫无铺垫的引入方式让很多同学无法接受。

知乎用户 @清雨影表示：「兄弟，我们是线性代数课，你不先介绍一下什么叫线性，什么叫代数吗？起手就是 n 阶行列式的定义，实力劝退。」

当然，指出这个问题同学不在少数。在其他关于线性代数的帖子中，我们也发现了关于该书「行列式」编排的吐槽。

知乎用户 @李佳繁表示：「行列式的定义给的很早难道不会让你感到很突兀和很没有必要么？！而且行列式是线性代数中几乎最为重要的概念之一，一上来就只是用数学语言给他了一个规定，在学线性代数的初期，能体会到什么？」

还有同学指出，这个问题并不是同济版《线性代数》所特有的，而是国内线代教材的通病。

在第一章讲完行列式之后，该书随后介绍了矩阵及其运算、矩阵的初等变换与线性方程组、向量组的线性相关性、相似矩阵及二次型、线性空间与线性变换几个章节。

除了行列式出现在第一章，其余的编排不合理之处还包括：

1）逆序数出现过早；

2）先讲矩阵再讲向量；

3）线性空间放到后面作为选学；

……

总之，这本书的编排顺序让很多同学摸不着头脑，学完之后也没有留下深刻的印象，甚至从此失去了对于线代学习的兴趣。

2、长得抽象，教材内容也抽象

除了结构编排的问题之外，「内容抽象」也是这本教材被吐槽的最多的点。

线性代数本身就是一门比较抽象的学科，因此，教材或教师理应通过各种方法帮助学生理解书中的抽象概念，比如运用图解的形式。但很多同学反映，书中的图解着实少得可怜，甚至「翻遍了全书，只有三个向量图解」（引自知乎用户 @Akiyama Mio）。

还有同学指出，很多概念的引入也是莫名其妙，没有具体的例子作为支撑，所以很多同学学完之后都不知道自己学的东西有什么用。

这本《线性代数》教材真的一无是处吗？有人持相反意见。这部分人认为，每本教材其实都有一定的适用人群，而且看书不一定要遵循书本的编排规律。

还有老师在评论区给出了这本书的原因：节省课时，能够满足考研需要。

想打下坚实数学基础，清华学生是这样学的

所以，既然线性代数这样学效率有点低，我们应该用什么姿势学习呢？

其实人们一直都在思考这个问题。去年，清华大学将「线性代数」科目的课本改成英文教材就引发了人们的热议。据介绍，该校改用了麻省理工学院（MIT）数学系教授 Gilbert Strang 的《Introduction to Linear Algebra》，效果怎样或许一时无法量化，但看起来蛮受欢迎的。

在 B 站上，Strang 老爷子总共 27 个多小时的「线性代数 MIT 18.06」课程也已达到了 73 万的播放量（其中一个资源的数据），可以说是 B 站最火的英文《线性代数》课程了。当然这门课程在国外也是 MIT 最热门的课程之一。根据 OCW 官网统计的数据，自 2002 年第一次发布以来，该课程的总访问量已经超过 1000 万。

为什么他的教材、课程那么受欢迎？从人们的评论中，我们可以总结出几个关键词：

1、实用、难度适中

知乎上有个帖子专门讨论 Gilbert Strang 的线性代数教材《Introduction to Linear Algebra》。有人表示，「Strang 的教材更加面向实际应用，难度适中，比较注重从实际问题中培养数学直觉，比较适合工程学科学生使用。」

这点相对于国内一些教材区别很大。我们通常接触到的课本一般是先给出定义，然后是定理和证明方法，很容易让非数学专业的学生失去兴趣。而 Strang 教授的教材则是「先告诉你一些有意思的数学事实，之后告诉你我们怎么解决那些问题之中较为简单的（有一部分方法甚至是依靠尝试和数学直觉），再和你一起探究这么解决为什么对，是否存在理论基础，留一些习题让你自己去试试它真的是对的，最后再做其他的深入探究，并提炼为定理。」（引自知乎用户 @李佳繁）

2、化抽象为具体

对于数学基础不好的人来说，「线性代数」真的是一门非常抽象的课程。但从大家对 Strang 教授《线性代数》教材的评价来看，比较一致的观感是「不是很抽象」，甚至可以「和高中对接」。Strang 教授对线性代数的讲解过程中会插入很多例子，能让学生结合例子理解一些抽象的概念，对非数学专业的学生非常友好。有同学表示，「感觉很多概念不再是死记硬背了」。

此外，整个课程的逻辑也是循循善诱式的，它「不是上来告诉你这样做是对的，而是一步步引导你让你理解就应该是这样子。」

Strang 教授 1934 年生于芝加哥，在加州大学洛杉矶分校取得博士学位，从 1962 年起就开始担任麻省理工学院的数学系教授，一辈子都在教书育人、笔耕不辍。去年初，他还出版了一本新书《Linear Algebra and Learning from Data》。

今年在新冠疫情期间，全球大多数地区的学生都无法前去教室上课，已年满 85 岁的 Strang 教授又把自己的线性代数课程视频更新了一版（课程大纲见下文）。

如果对于英文教学不太感冒，有人表示蓝以中的《高等代数简明教程》、丘维声的《简明线性代数》也是不错的选择。

如果你在自己学习线性代数时有些迷惑，根据课程视频整理自己的思路可能是效率最高的选择。

Strang 教授最新「线性代数」课程大纲

目前，Strang 教授更新的线性代数课程只有 5 个讲座，但在此之前，原 2011 年的经典版本是专门为自学人员所设计，已发布在 MIT 的 OCW 平台上，包含 35 个讲座视频以及 36 个助教辅佐类讲解视频。感兴趣的读者可以结合着看。

下面我们来看看课程大纲：

1、导论：了解线性代数的新方式

Strang 教授在导论中表示，他开设这一门课程的目的是让大家了解奇异值的概念，这是线性代数中特别重要的一个知识点。他将矩阵分解为两个或三个部分，以方便我们更深入地了解其性质。

2、矩阵的列空间与向量空间中的基

Strang 教授从矩阵的列空间开始，带我们走进线性代数的世界。

这节课还讲解了列空间与行空间的基：

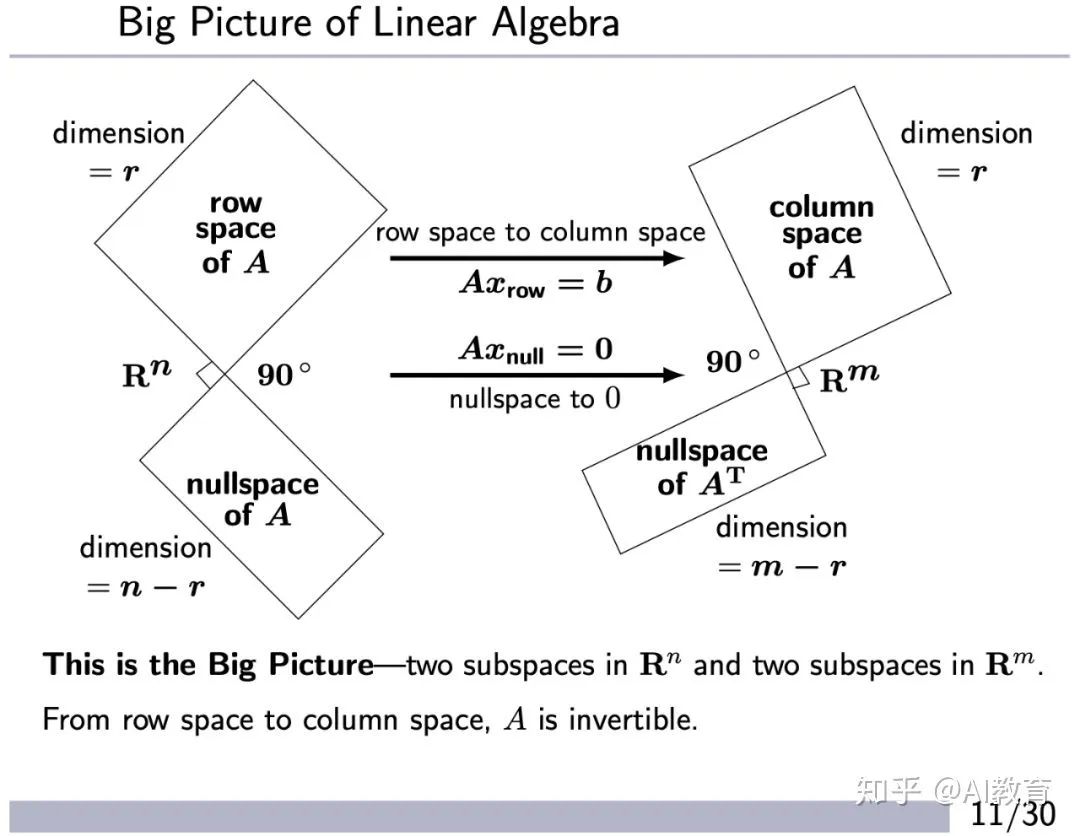
3、线性代数的 Big Picture

Strang 教授在这一节中讲解了 A 的行空间、列空间、零空间、A^T 的零空间，以及这四个子空间之间的相互关系。

4、正交向量

在这一节中，Strang 教授讲解了正交向量、正交矩阵及其子空间，其中涵盖了 Gram-Schmidt 正交化与最小二乘。

5、特征值与特征向量

特征值与特征向量是深入了解矩阵性质的重要方式之一，它们在工程与研究领域都有很多重要应用。

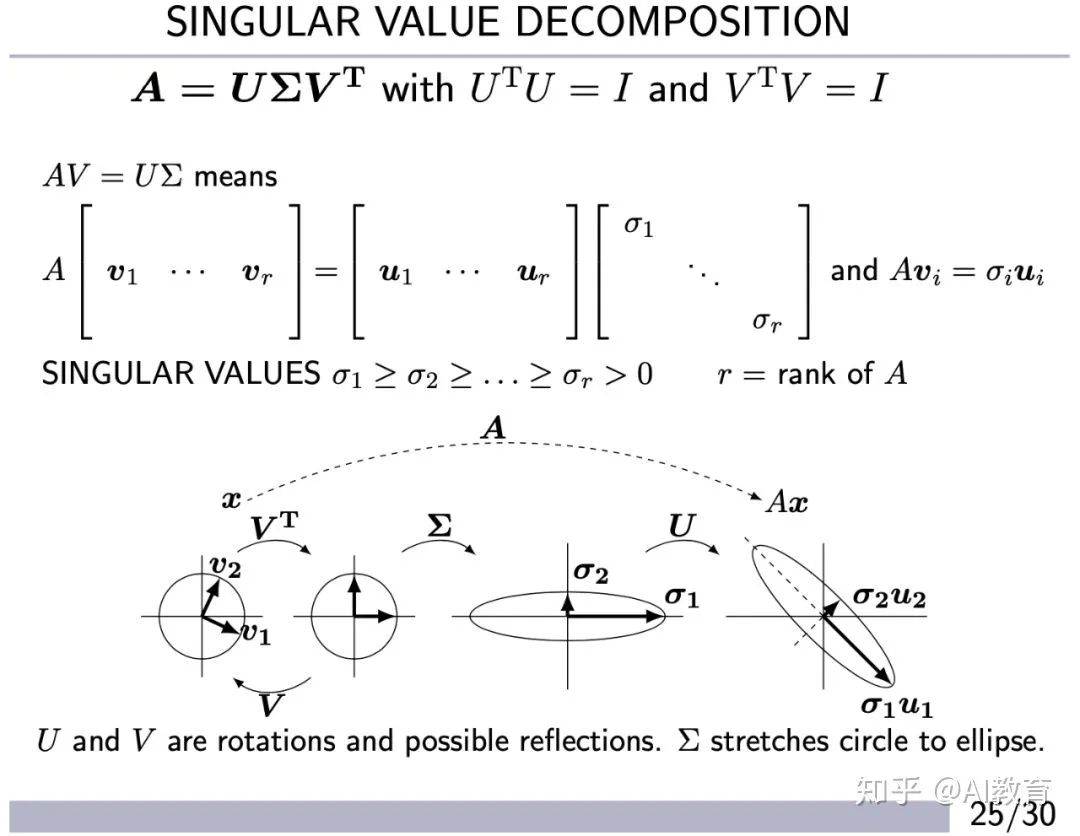
6、奇异值与奇异向量
在机器学习中，数据矩阵不是方阵，因此它们需要使用不同于特征值的另外一种方法：奇异值分解（SVD）。奇异值分解用奇异值和向量表示每个矩阵。

最后需要说明的是，除了视频和 PPT 之外，这门课程的每节课都有相应的文字稿作为参考，可以说对英文听力不好的同学非常友好。

美国学生学的数学那么简单？为何又那么优秀？

看到这里，不知大家是否会有个疑惑：为什么明明被公认为数学基础好的中国人，到了大学学起数学反而更加吃力了，但看了美国教授的数学课程就能打开「新世界的大门」；而且快乐教育下的绝大部分美国人数学这么差，为什么还能出那么多厉害的教授、数学家和科学家呢？

一位昔日「美高党」Dave Geng 是这样说的：「美国给予不热爱数学的学生最基础的数学教育，而给予热爱数学的学生最高水平的数学教育。」

首先，先说「美国给予不热爱数学的学生最基础的数学教育」。
美国的每个地区，对于，比如，高中毕业的学生，应该有何种的数学修养，大多是有硬性规定的。比如麻省，每年对特定几个年级的学生有统考，这个统考的主要内容之一就是数学，数学不过关的，高中是不允许你毕业的。所以基本上每间正规高中，也都对数学水平有最基本的要求才准毕业。据我所知，这个标准大概在会运算简单的三角函数就可以了。这个水平，以咱们中国的标准来看，确实不算高，而且很多人还都是勉强混过去的。（高中课很松。。。）
这种低要求的直接结果就是，美国 99% 的学生（99% 这个数字并不夸张，可能更高）的数学都停留在生活勉强可以自理的水平上。
好了，到了说「给热爱数学的学生最高水平的数学教育」的部分了。
以高中为例，对于一些数学比较好的不安分分子，为了安抚他们，不给社会添麻烦，学校（不是每间学校都有这个条件）会提供 Advanced Placement 课程，也就是宅男们喜闻乐见的 AP课程。以数学为例，高中最高级的 AP课程，叫做 BC微积分，2005年我上高中的时候，课本是下面这个：

我们的任务则是把这本书，从头到尾学得通通透透。值得注意的是，只要你前面的课程成绩都好，你几年级修这个课是没有限制的，我上学时班上最年轻的同学是一位俄裔美国人，他修此门课程时才上十年级（相当于我们高一），他最后这门课的成绩是 A+ ，在我们学校，意味着每次考试的成绩，都在 95 分以上，实在是学校「公害」。

这本书的内容，大家都可以查到，人家高一就学这个，各位自诩为学霸的，颤抖了吗？基本上到学矢量微积分之前，学完了这本书，你做微积分已经应已如四则运算般自如。

说到这就差不多了，中心思想和开始提到的一样，可能论数学物理的平均水平，美国学生确实远远不如中国学生，但是谈到「给天才 / 有兴趣的人的教育」时，中国的教育制度，则还停留在解放前。而到了大学，这个差距就越拉越大，到了研究生阶段，没有鄙视国内读研读博的盆友们的意思，但与美国的「高高等」教育相比，真的无法相提并论。
这样的制度，从侧面看，很大一个好处就是，年轻人可以把多余的时间和精力，专注到自己喜欢做的事情上。很多比较聪明的宅男，高中最后一年基本没有什么数理课程了（全提前学完了），学学哲学，历史，艺术，玩玩乐团，体育，对成长都有帮助。前面那位俄裔学霸，还是该地区的长跑冠军。
另外一个好处就是，学霸们可以和学霸们在一起玩一起上课一起耍，不要小看这些宅男们，学霸们聚在一起的能量们是很大的，你没发现，在你们现在打工的地方，老板们年轻时都是学霸吗？

再说说小学数学。

我们所学的数学，很多都是通过套用公式来一遍又一遍的做题来证明公式的正确性。可是美国小学的数学不一样。

他们通常都是学数学来解决问题，会套用在实际的生活中去学习。比方说，今天学习数字 3。一个消防员站在一棵高高的树下，树上有两只小猫被困在上面下不来，消防员要去救小猫，怎么救。首先选一下可以使用的工具，灭火器？捕蝴蝶的网？还是梯子？因为树高要用梯子，好，几个梯子才能够到？一个不行，两个，三个呢？

再引用一个朋友孩子的例子。他儿子上 3 年级，以我们的眼光粗粗来看，他们学的是：

1）10 以内的加减法

2）1000 以内数字的读写

这是什么级别？好像现在幼儿园中班就已经教这个了！

但我朋友花了 3 小时教材，越看越汗，还特地总结了一下他们教的我们没教的：

1）同样从 1 数到 10 再 11，我们是单纯的数，数到10,100,1000；但他们数到 11 后，开始讲进位、十进制，开始引入二进制、五进制等；

2）讲 10 以内的数字，区分数字的用途，同样是数字 3，可以是 3 个房间，第 3 间房，房间长 3 米，他们有什么不同？

3）在数字的用途一节后需要写 paper：我们说华盛顿有人口 3，454,456（数字是我随便编的），这个数字是精确的嘛？还是估算的？为什么？怎么证明？

4）有一些逻辑题目，类似于“教授的隔壁是医生医生喜欢蓝色” 这种问题，我们孩子是从小作为智力题目来做的，他们则介绍了只需要用到 1-10 这几个数字的表格，介绍如何将这些条件填入表格，最后如何出答案。

其实还有更多....

总体感觉这个的教材：

1、强调数学的基本概念。

2、强调逻辑思维。同样是逻辑问题，我们一直强调的是用脑子解决，会的就真是个聪明的孩子，不会就你怎么这么笨。而他们从小就拿出来，教孩子用工具解决。国人一向号称自己是最聪明的民族，但创新实力却很弱，我相信我观察到的这一点是原因之一。

3、细致。我们长大后，看老外的文档，事无巨细，是不是特别佩服？可为什么我们从来没有耐心看下去，写出来呢？我想，这就是原因，我们都没有耐心为孩子细致的解剖这个世界，孩子长大后怎么能细心？

总之，美国的教育更注重的是在大学前开阔视野，找你所喜欢的、感兴趣的领域和学科，所以他们一直到高中都有很多自己选修的课程，很多很多课，看似很轻松，学自己喜欢的嘛。当我们经历过那不想回去的高考之后，全都瞬间解压，觉得没什么事做了，开始玩乐，但美国大学生却非常辛苦，学习努力，这不光是因为他们的大学不好毕业，而是，大学时期其实才是真正学习的好时光，术业专攻，之前都在寻找培养兴趣，拓展视野，找到自己的兴趣所在。所以，可见的，他们的数学简单，其实不是简单，只是我们学过的很多数学公式，现在生活中也都不会用到了。

所以说「美国学生学的数学比我们简单」这就是个伪命题，不存在这样的事情。此外，提到这一点也并不是为了贬低中国的教育制度（中国基础教育制度优越性是毋庸置疑的），而是为了告诫今后打算从事或已苦苦挣扎在数学学习事业中的各位童鞋们，不管在中国还是美国，想要在数学学术上有所建树，首先就是要培养兴趣，其次就是要刻苦学习，找到适合自己的学习方法！

作者简介：武汉维识教育科技有限公司专注于人工智能、机器人工程、智能制造、云计算、大数据、区块链、信息安全、互联网营销、健康护理等多领域、多层次「新工科」「新职业」人才培养与输送。公司立足湖北科教大省，辐射全国，提供专业共建、师资培训、联合实验室、科研项目合作、实习实训就业、职业技能培训等整体解决方案。同时与诸多产业领军企业建立战略合作关系，融合产业先进技术，为金融、医疗、教育、安防、交通、零售、制造、农业等行业用户，提供多维解决方案。在全国众多院校、企业、研究机构、投资界等多方合作发展中发挥纽带作用，为推动相关领域人才培养和产业发展贡献力量。

——The End——

在看