奠定高斯数学王子地位的20个论据
极市导读
高斯，以一己之力推动人类知识的边界线。 >>加入极市CV技术交流群，走在计算机视觉的最前沿
01
02
没想到高斯一下子就给出了正确答案，是 
. 而且还解释了解答方法，那就是首尾相加，而现在 等差数列 的求和公式
03
高斯在 11 岁时独立推导出了 牛顿 的 二项式定理
04
高斯在 14 岁的时候研究了下述数列：
，
，
. 如下递推地定义数列 
：
，
皆收敛，且极限相等， 此极限称为 
和 
的 算术几何平均值，记作 
. 高斯还给出了 的表达式：
的快速算法，这种算法就是目前计算圆周率最快的算法之一的 Salamin-Brent 算法：
， 
. 则
05
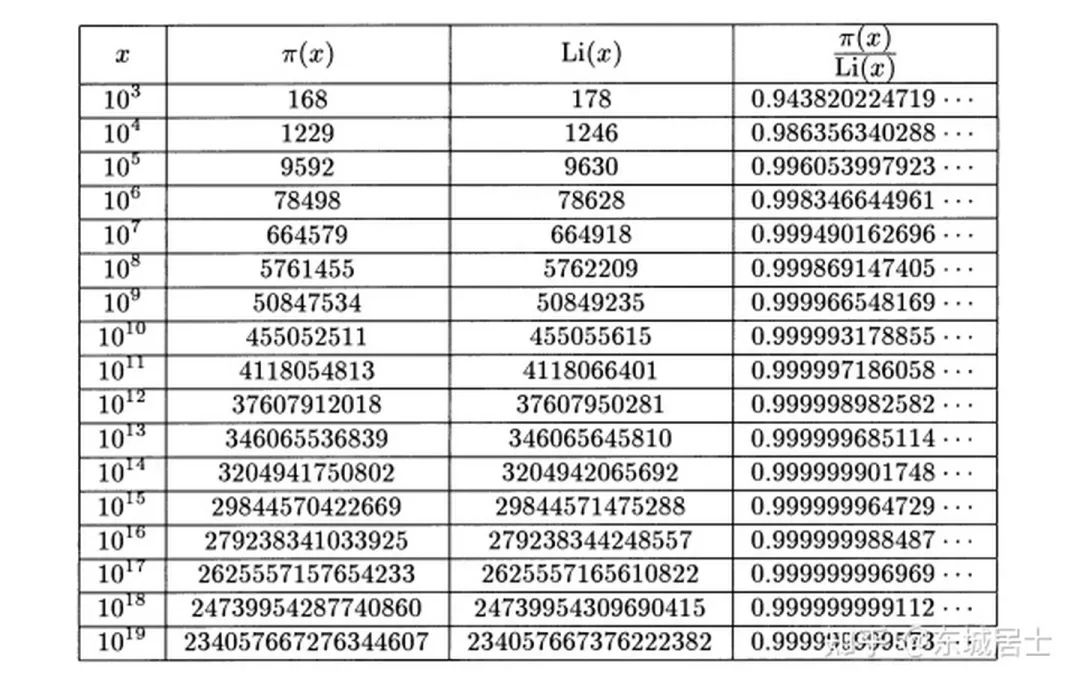
个，他惊讶地发现素数的分布密度接近于对数的倒数，这一发现就是就是著名的 素数定理：
06
可以用根式表达出来，高斯经过一顿巧算得到
形边可以尺规作图当且仅当 
，其中 
，而 
， 
， 
， 
为两两不同的 费马素数.
种不同的证法，每一种证法都包含了重要的数学思想. 后来他又发现了 四次互反律：
个三角数之和.
个平方数之和.
时，每一个正整数都可以表示为不超过 个 角数之和.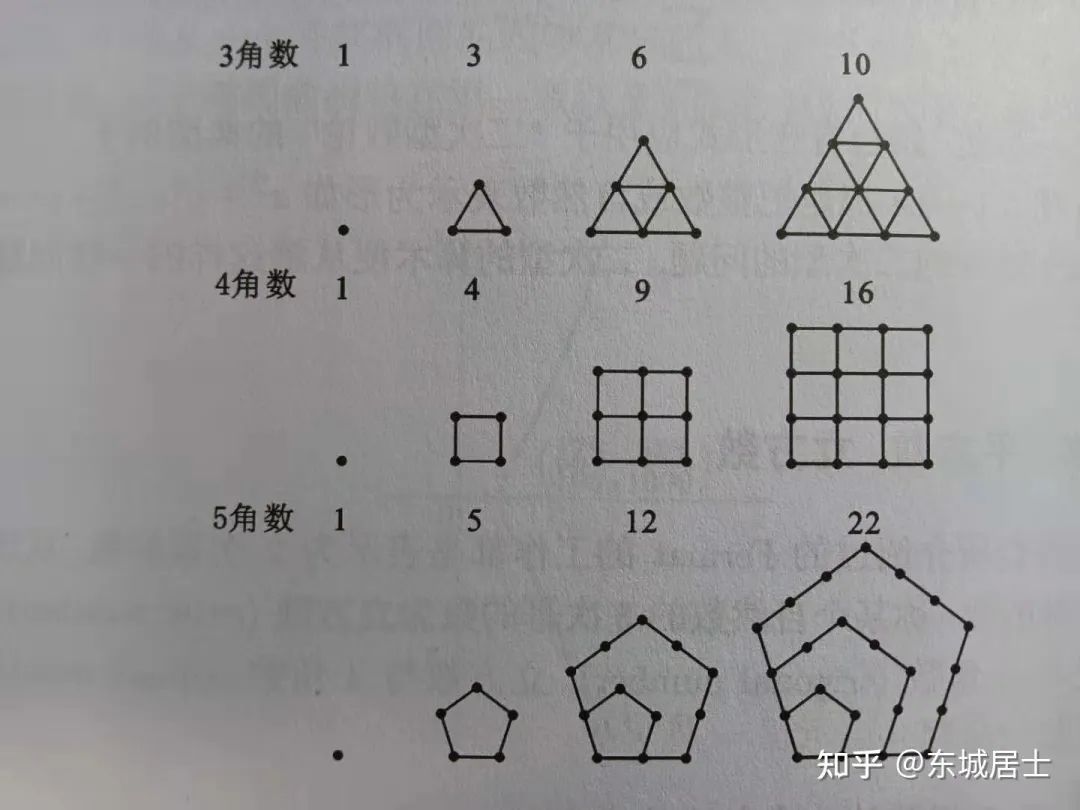
上的方程 
，此方程只有有限个解，我们将其解的个数记为 
. 那 的值是多少呢？高斯给出了下述答案：
为素数，则
时，
满足 
，且 
.
时，
时，显然有 
，从而
时，显然有 
，从而
07
， 
.08
09
10
11
和 
，我们称 
为 高斯曲率，其表达式为
时，也就是 
为测地线时，Gauss-Bonnet 公式变成
为测地三角形 的内角，即 
，则上式等价于
，它与 之差恰好为曲面的高斯曲率 
在测地三角形所围成的区域上的积分，因此欧式平面几何学与一般的曲面上的几何学的本质差别就在于空间本身的弯曲性质不同，这是 欧式几何 与 非欧几何 的根本区别.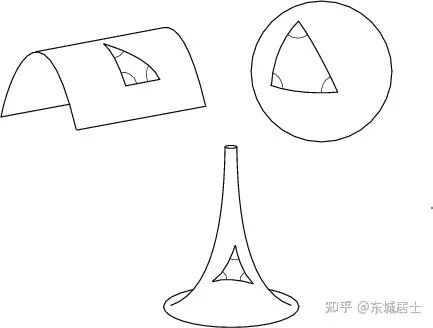
）与拓扑学的不变量（欧拉示性数 
）联系了起来，它在高维情形的推广就是著名的 Gauss-Bonnet-Chern 定理.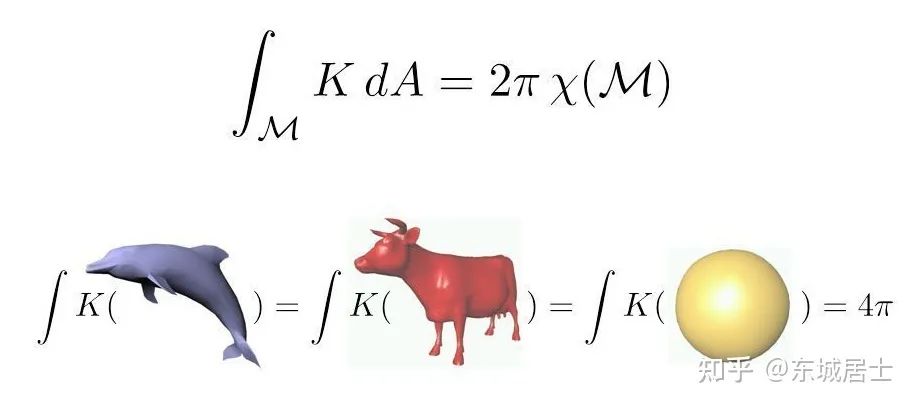
12
13
无平方因子，则域 
为 二次数域，当 
时称 为 实二次数域，当 
时称 为 虚二次数域.
的 类数 为 
，但对于是否还有其他类数为 的虚二次数域一直无法做出回答. 这个问题直到 1966 年才由数学家 Baker 和 Stark 解决，那就是类数为 的虚二次数域只有高斯给出的那 
个，Baker 和 Stark 由于此项工作而获得了菲尔兹奖.
的虚二次数域的个数 
是有限的. 1971 年，Baker 和 Stark 证明了 
. 到 1983 年，Goldfeld，Gross 和 Zagier 最终证实了高斯的猜测. ，使得 的类数为 .14
，这是概率论与数论统计学中最重要的分布. 因此现在我们也把正态分布的密度函数
15
类似的常数 
！我们都知道圆周率 是圆的周长与直径的比，其实数学中还有下面这种曲线：
的 Bernoulli 双纽线，简称为 双纽线.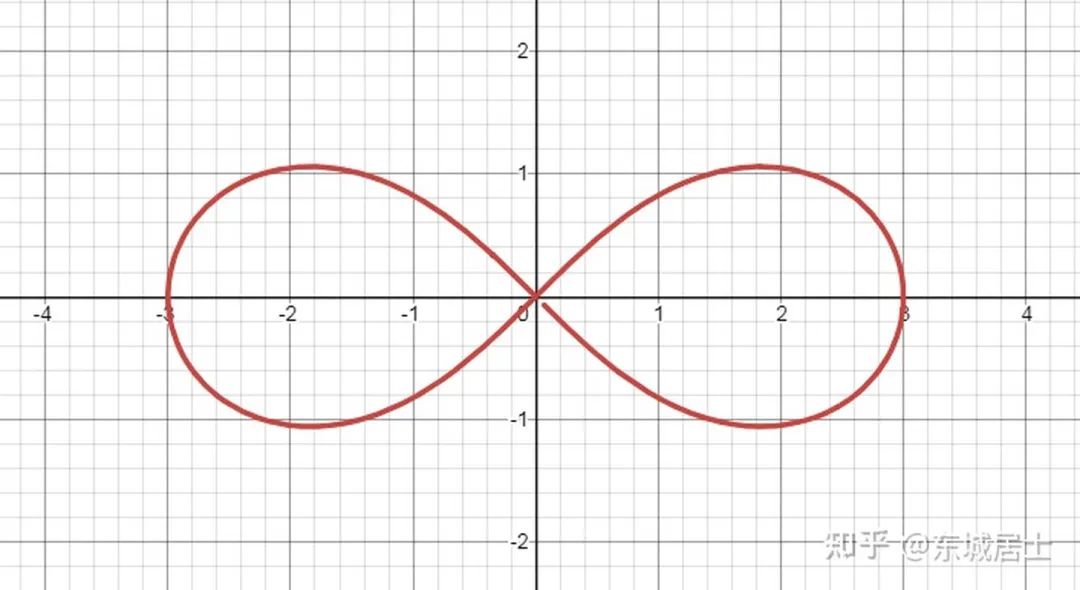
，现以极径 
为参数，可得 双纽线 的周长为
. 由上面的推导可知
和 长的像两兄弟，不仅如此，它们还有类似的积分表达式
还与下面这些级数有关系.
16
. 出发的测地线与以点 为中心的测地圆是彼此正交的.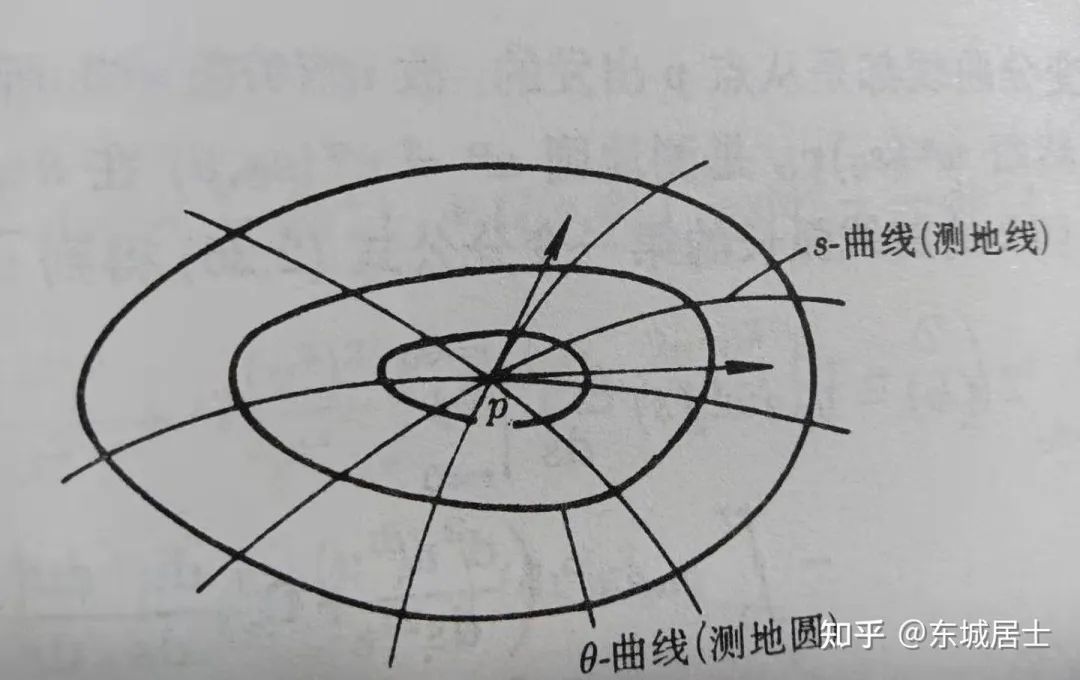
17
18
19
20
推荐阅读
2021-03-03
2021-03-02
2021-03-01
# CV技术社群邀请函 #
备注：姓名-学校/公司-研究方向-城市（如：小极-北大-目标检测-深圳）
即可申请加入极市目标检测/图像分割/工业检测/人脸/医学影像/3D/SLAM/自动驾驶/超分辨率/姿态估计/ReID/GAN/图像增强/OCR/视频理解等技术交流群
每月大咖直播分享、真实项目需求对接、求职内推、算法竞赛、干货资讯汇总、与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度等名校名企视觉开发者互动交流~
评论