B树自在人心
B树自在人心之B-树 和 B+树
3.30
简介
首先要搞清楚一点,他们的名字读法,B+树读作B加树;B-树 读作 B树 ,不是B减树,没有B减树这个说法的。就只有B-树和B+树这俩种数据结构,B-树是由B-Tree翻译过来的,中间不是减号。。。。别出去跟别人说精通B树,B+树和B减树,hahahaha。
在看B树之前,相信你已经知道什么是二叉树、二叉排序树、平衡二叉树、最优二叉树等等。接下来我们先看看B-树吧。
3.30
B-树
2.1 为什么会出现B-树?
2.2 B-树的定义
先看一张B-树的图,再根据图来看定义,这样你会开朗许多。
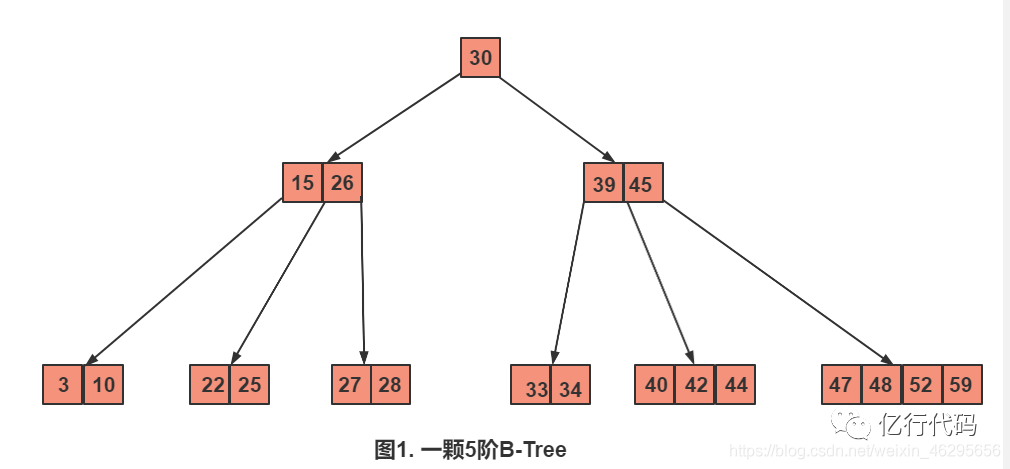
接着再来看下有关B-树的定义。
一颗m阶的B-树应满足以下条件:
每个节点最多只有m个子节点。
如果根不是叶节点,则根至少有两个子节点。
所有叶子都出现在同一层,没有任何信息(高度一致)。
每个节点中的元素从小到大排列。
每个非叶子节点(除了根)具有至少⌈ m/2⌉子节点。
每个中间节点都包含k-1个元素和k个孩子,其中 m/2 <= k <= m。
条件很多,大脑爆炸!莫急,我们看图分析一波。
首先上图是一个5阶B-树,为什么是5阶?阶树怎么看? 看哪个节点中元素最多即可,例如上图中 ,【47,48,52,59】这个节点中元素最多,有4个元素,因为该节点下可以引出5个分支,所以该树是5阶B-树。(严格地说这样来判断B-树的阶树是不严谨的,因为一般一颗B-树的阶树是人为规定好的。B-树的阶树就是存储每个节点数组的长度加一,每一个节点中存储的数据长度是一致的,只是将没有数据的位置省略了,如果我们把59这个元素删除了,但是我们还是认为这是一颗5阶B-树,这是人为规定的,数据没了,但位置还在),就像下面这样:
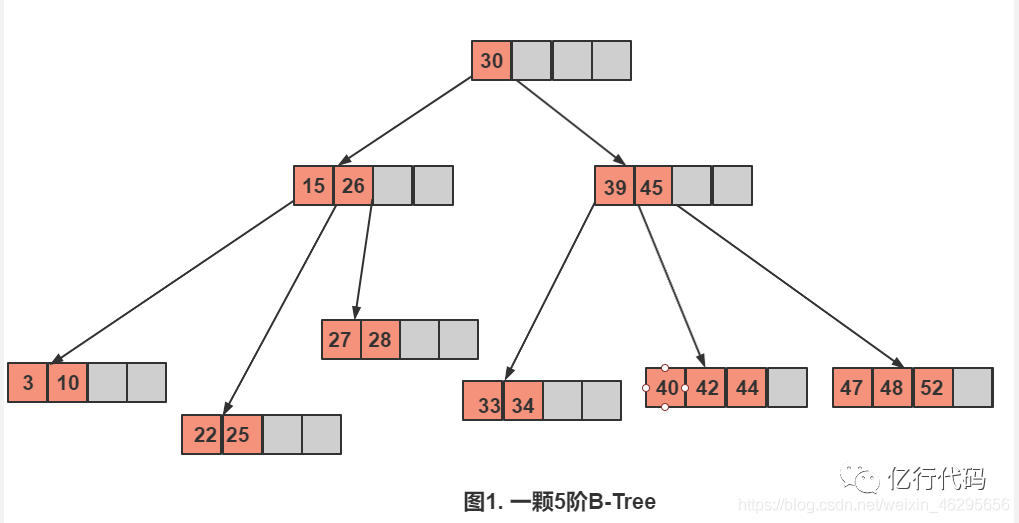
我们看下【15,26】这个节点,它有两个元素15和26,有三个子节点【3,10】、【22,25】、【27,28】。这三个属于叶子节点,在同一层,并且大小是递增的,3和10小于15 , 22和25在【15,26】之间, 27和28又大于26,看出规律了吧, 左节点 < 根节点 < 右节点。
2.3 B-树的查找
下面,我们以该树为例,来查找一下关键字吧!
查找44:
第一步、先扫描根节点的所有元素,扫描完了没有找到。
第二步、沿着右分支,在该节点继续从左往右扫描,找到了第一个大于关键字的元素。
第三步、沿着该元素的左边的分支,又在该节点上继续从左往右扫描。最后找到。
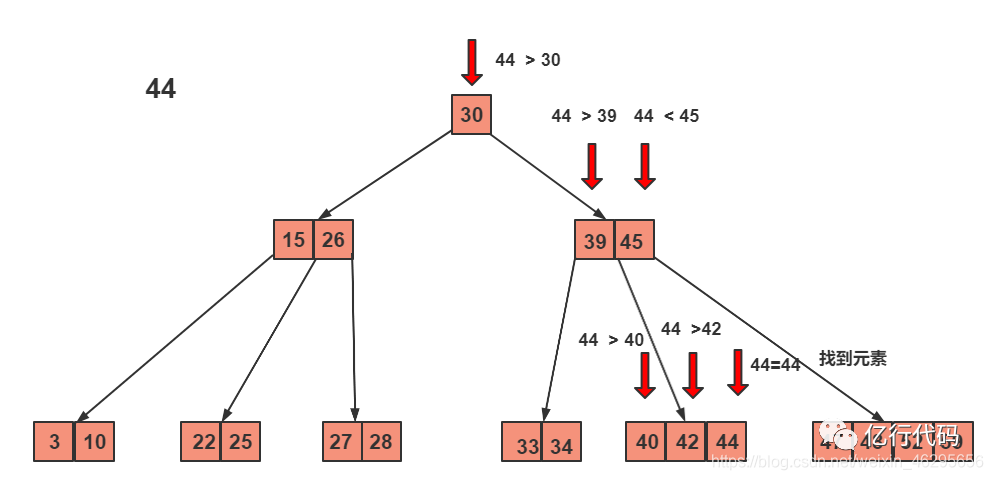
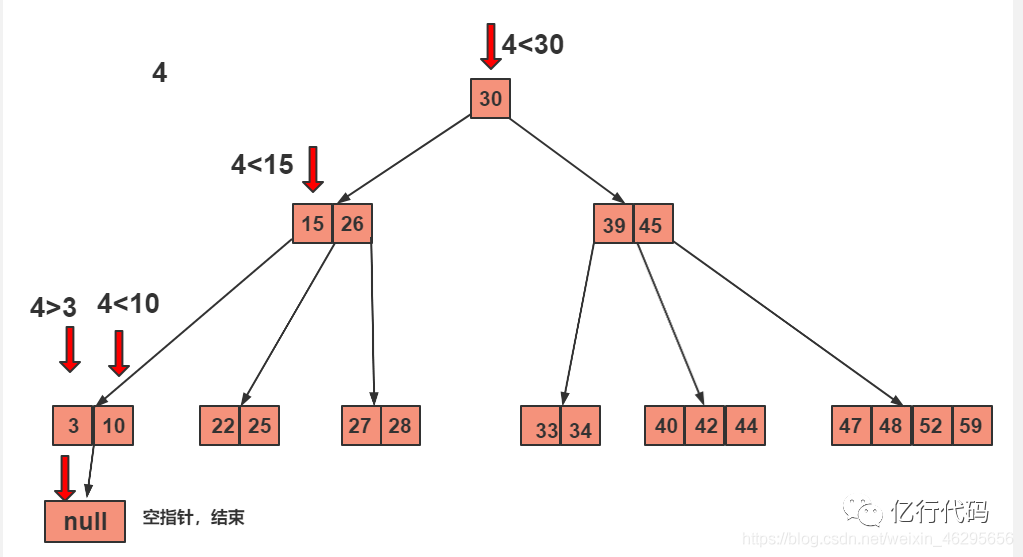
再来举个例子,查找关键字4:
查找方法都是一样的,注意最后,10元素下面没有元素,指向位空,查找失败。
2.4关键字的插入
我们通过一道题来弄清楚B-树关键字的插入。
例题:
用以下关键字序列【1,2,6,7,11,4,8,13,10,5,17,9,16,20,3,14,18,19,15】创建**一颗5阶B-树**。
由于我们创建的是一颗5阶B-树,所以每个节点的关键字最大为4
第一步,取4前四个关键字

第二步、然后一个一个的插入元素。
插入11:
发现一个节点内有5个元素,不符合5阶B-树,则进行节点拆分。
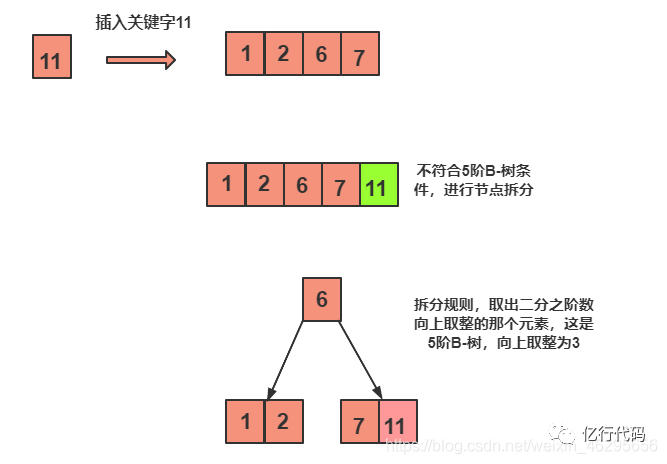
插入4:
首先要扫描,从6开始扫描,4 < 6 ,然后开始扫描左节点,扫描到2之后,4>2,又扫描2的右节点,发现为空,就将关键字4插入2的后边。
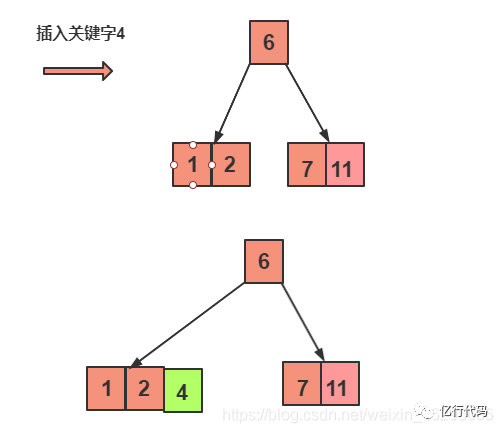
插入8:
步骤一样,先扫描6这个节点, 8 > 6 ,然后扫描它的右节点,发现 8 < 11,就将8插入11的左边。

插入13 :
从根节点开始扫描, 13 > 6 ,扫描右节点,到了11的右节点,发现为空,插入到11的右边。

插入10:
步骤一样,插入之后发现不满足5阶B-树的要求,进行节点拆分。

就变成了这样:
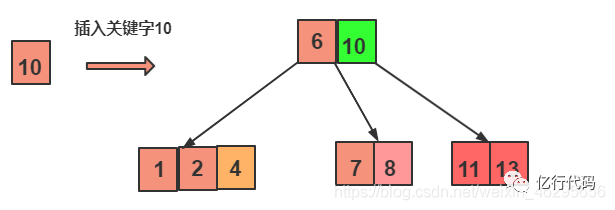
继续插入5:
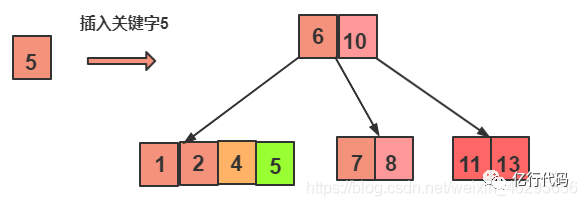
插入17:

最终将所有元素全部插入,得到如下一颗5阶B-树:
自己可以手画一下来加深插入的印象。
2.5 关键字删除
接下来看B-树的关键字删除。
我们就用上面这个5阶B-树来删除关键字吧。

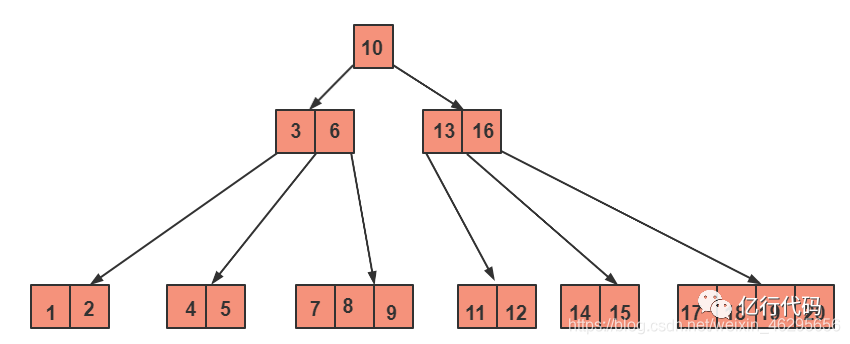
删除关键字8 :(注意节点和关键字的关系,一个节点包含多个关键字,关键字也可以叫元素,如图中【1,2】就是一个节点,1和2是该节点的两个元素。)
这里要删除8,要看看能不能直接删,因为要使删除之后的树,也要符合B-树的条件,即除了根节点之外,其余节点的分支树至少是二分之阶数的上取整(例如:这里是5阶,5/2上取整 = 3 ,即节点不少于三个分支,即每个节点至少有两个关键字,看图中,【3,6】和【13,16】这两个节点,他们都有三个节点,而且这样个节点的关键字都是二,符合条件)。
这里删除8之后,8在【7,8,9】这个节点里,删除了就变成了【7,9】,是符合5阶B-树的条件的。所以直接删。
删除之后变成酱紫:
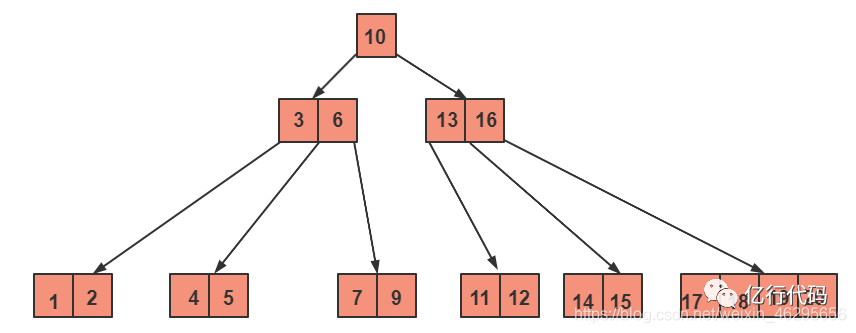
再来删除一个关键字16,
思路:注意这个关键字的位置,它是处于非叶子节点上,这种节点的删除方法是:用这个节点的左子树节点中最大的关键字或者右子树节点中最小的关键字来替换我们要删除的关键字即可。
以删除16这个例子来看下:

我们要删除16这个关键字,就看下它的左分支节点【14,15】,找到该节点最大的关键字15,替换16,但是你会发现一个问题,15走了,这个节点就只有14这一个元素了,显然不符合5阶B-树的要求。
我们再再来看看右分支【17,18,19,20】,找到该节点中最小的元素17,然后用17来替换要删除的关键字的位置 ,这样,节点就变成了【18,19,20】,符合5阶B-树的条件。
所以,删除16关键字之后,就变成了这样:

继续,我们来删除15关键字:
思路:如果直接删除的话,不符合B-树条件 ,我们就向其兄弟节点来借关键字:父结点中17下来,18上去,然后删除15关键字。

再来删除一个关键字4:
这时候用上面向兄弟节点借那种方法就行不通了,因为它的左右兄弟节点都到下限了(如果借了,就不符合B-树条件)。
那么怎么删除呢?我们直接删除!然后再进行一次节点的合并操作。
具体步骤如下:
第一步、删除关键字4:

第二步、**兄弟节点合并**,一般都是和节点元素较少的那个节点合并,这里左右节点元素都相同,所以左右均可。
合并右节点:
合并步骤:将需要合并的节点的父结点移下来,然后合并,并不是直接将左右节点合并噢!
最终变成这样:
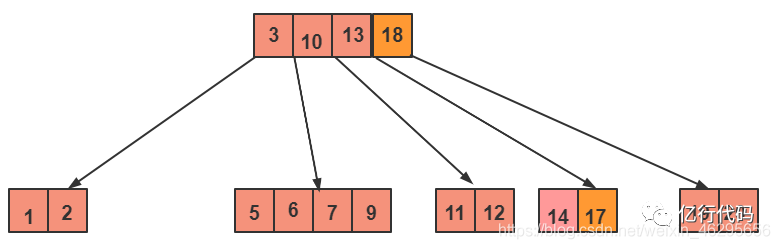
同理,合并左节点:

这两种结果均可,从这里可以看出, 当我们删除关键字的时候,可能导致不同的结果。
3.30
B+树
B-树看了之后,咋们再来看看B+树。
B+树是对B树的一种变形树,它与B树的差异在于:
有n个关键字的节点就有n个分支(在B-树中有n+1个);
· 非叶结点仅具有索引作用,跟记录有关的信息均存放在叶结点中。
· 树的所有叶结点构成一个有序链表,可以按照关键码排序的次序遍历全部记录。B+树的非叶子结点只包含导航信息,不包含实际的值,所有的叶子结点和相连的节点使用链表相连,便于区间查找和遍历。
请看图,这就是一颗B+树:
特点:每个节点中每个元素只引出一个分支,并且是指向子节点中的最大值;所有叶子节点由指针连接,构成一个有序链表。

B+树的内部节点(即非叶子节点)上不包含数据信息,数据全部存放在叶子节点上,并且每个节点用指针连接,这样访问叶子节点上关联的数据也具有更好的缓存命中率。
B+树的查找效率是极高的,在Mysql中MyISAM存储引擎就是用B+树实现的。
B+树就聊到这里吧!下篇博客我们再来详谈MySQL的存储引擎,文章有错请及时指出。
如果该文章对你有帮助,"再看"和"点赞"是对我最大的鼓励!
扫二维码|关注我们
谢谢观看

把城市夜晚的喧嚣,点出来
▼
