如果你愿意一层一层地剥开“递归”的心

引言

如果你愿意一层一层 一层地剥开我的心 你会发现 你会讶异 “返回条件”是我 最压抑 最深处的秘密 --- 递归函数写给程序员的歌。

ISCP 中说到递归，用了一句话：Leap of fatich。——信仰的跳跃。指的是程序设计思想的转变，使递归成为编程思想的一部分。既然是跳跃，说明其与常见编程思想之间存在差异。

无论是顺序、分支、循环、函数还是类，哪怕是函数式编程，其思想大体还在常人思维、生活经验范围内。但递归不是这样：递归是在数学、机器上进行了较多假设和设计，理解起来较为困难。本文尝试用 Python 来理解递归。

简单地说，递归是函数中继续调用自身。比如写一个函数，让阿甘快跑。

def gump():    print('Running...')    gump()

运行这个函数，如下是这个函数运行和捕获异常的结果。

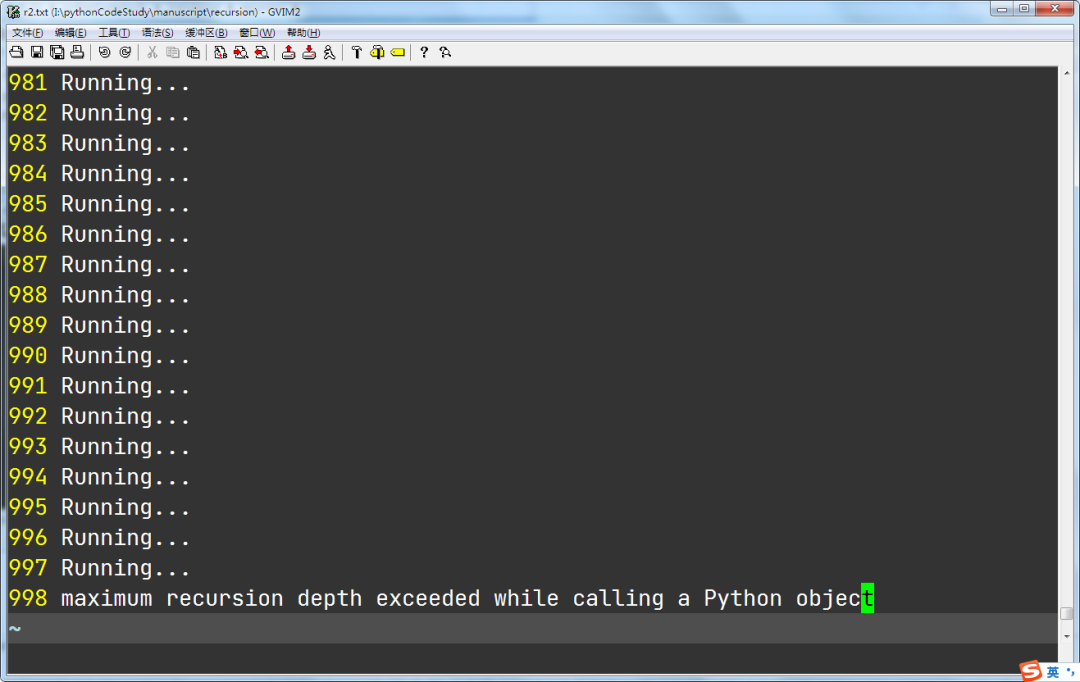
程序在输出 997 个 Running 之后，报出了 RecursionError 异常。其具体信息是：”maximum recursion depth exceeded in comparison“，也就是超过最大递归深度。

超过最大递归深度：就是超过算机设置的递归层次限制。在堆栈类设计的程序语言（Python 就是基于栈的虚拟机）中，就是突破了调用栈的高度，这种异常称为 Stack Overflow（栈溢出），这也是 IT 界著名网站 Stackoverflow.com 的命名来源。

以上的程序 gump 函数中调用了 gump，这个函数就是递归函数。但是这个递归函数没有什么用处，要写一个有用处的递归函数，需要满足如下三点。

定义递归函数的三点

定义一个递归函数，需要指出初始化条件、结束条件、上下层变化关系这三点。我们以阶乘为例，来一步步定义这个函数。

首先，我们小学二年级就知道 5 的阶乘的定义是这样的：5!= 5*4*3*2*1，代数公式是 n!=n*(n-1)...*2*1 ，进而我们能推出如下的公式：n!=n*(n-1)!

其实，是先发现了递归公式，才能有递归函数。根据这个公式，我们就可以写出求阶乘的递归函数了：

def factrial(n):    if n <= 1:        return 1    else :        return n * factrial1(n-1)

在这里，三个条件是这么定义的。

初始条件：定义函数def factrial(n):这里的 n 就是需要求的阶乘。

结束条件：也就是递归函数调用到最后（末、深）时的终结条件：if n <= 1:return 1。这其实相当于求 1!的结果，就是 1。

定义上下层之间的变化关系：意思是定义递归函数的调用关系，也就是上层是怎么（深入）调用下层的。这里是：return n * factrial(n-1)。

我们把这三个条件组装起来，就构成了求阶乘的递归函数。首先写终结条件，便于递归函数终结，然后写变化关系，构成递归函数。

调用测试，factrial(5)结果为 120。结果正确，运行成功。

递归相关特性

Python 中递归栈高度的设置

第一个实例程序中，当我们超出了系统的限制后，递归调用会报出栈溢出错误。那么这个限制是多少呢？可以用这个命令查看：import sys;print(sys.getrecursionlimit())。而且这个值是可以设置的：sys.setrecursionlimit(6)。这规定了函数调用栈的最高高度。

尾递归优化

如上求阶乘的程序中，最后一句话中的return n * factrial1(n-1)可以看出，这是一个表达式。这个表达式是求乘法，其中一个参数是常数，另一个参数是函数调用的结果。也就是说，这个表达式是延迟求解的：只有等程序进入执行，并返回结果后，才能再返回给更上一级结果。

更容易理解的是，假设我们是一个 CPU，我们在这里需要深入 factrial1(n-1)，进而深入 factrial1(n-2)一直深入到 factrial1(0)，才能产生一个确定的结果，返回给上一级调用函数，再返回给更上一次的调用函数。也就是我们进入了函数调用链，然后再原路返回各个结果。

无疑，如上这个复杂的过程是低效的。怎么加速呢？方法就是尾递归优化：在调用函数式，不使用表达式，直接调用函数。

def factrial2(n,base = 1):    if n <= 1:        return 1     else:        return factrial2(n-1,n*base)

以上是尾递归优化后的阶乘函数。但遗憾的是，Python 并不支持尾递归优化，所以在 Python 中执行如上代码，效率并没有得到提高。在其他诸如 C 或者 JavaScript 的语言中，这种写法可以提高效率。大家掌握思想即可。

那么，有没有优化递归的方法呢？

缓存优化

分析递归函数的执行过程，我们很容易发现：递归函数都在重复执行之前的计算。以 factrial1(5)为例，它在执行时，多次执行了 factrial1 函数，但是这些调用的参数只有六种：0 , 1 , 2 , 3 , 4 , 5。如果能够缓存每次运算的结果，想必会比每次重新计算要快。

我们作如下修改：

rs = [1, 1]def factrial3 (n):    try:        return rs[n]    except:        if n <= 1:            return 1        else:            rs.append(n*factrial3(n-1))            return rs[-1]

程序 factrial3 定义之前，首先定义了全局变量 rs，他会保留函数不同参数的计算结果。当调用时，首先判断 rs 变量中有没有这个暂存的结果，若有，直接采用，若没有则计算之。

Python 标准库中的 functools.lru_cache 装饰器，正是采用这个机制，来实现递归加速。使用装饰器的代码是这样。

import functools
@functools.lru_cache()def factrial4(n):    if n <= 1:        return 1    else:        return n*factrial4(n-1)

如上代码，真的能加速递归调用么？我们采用如下代码测试：

import timeitprint(timeit.timeit('factrial1(10)',globals=globals()))print(timeit.timeit('factrial2(10)',globals=globals()))print(timeit.timeit('factrial3(10)',globals=globals()))print(timeit.timeit('factrial4(10)',globals=globals()))

结果如下：

1.74919749955135862.0833343959732070.121600316988066390.11237836531568357

可见：

•一、对比前两个函数可知，尾递归优化后的函数并没有加速。•二、自编写的缓存优化，作用很大。•三、系统自带的@functools.lru_cache()装饰器，效果和自编的缓存优化相差不大。

总结

本文分析了递归的含义，及定义递归函数的三个注意事项。分析了递归的栈高度设置，介绍了尾递归优化，分析了 Python 标准库中缓冲装饰器的设计思想。

递归在程序设计中，有很大实用意义：深刻掌握递归，是我们理解程序设计思想、理解遍历树的重要基础。

赞 赏 作 者

点击下方阅读原文加入社区会员