一文弄懂各种损失函数(loss function)
朴素贝叶斯: 最大化后验概率
遗传编程: 最大化适应度函数
强化学习: 最大化总回报/价值函数
CART决策树分类: 最大化信息增益/最小化子节点不纯度
CART,决策树回归,线性回归,自适应线性神经元…: 最小化均方误差成本(或损失)函数
分类模型: 最大化对数似然或最小化交叉熵损失(或代价)函数
支持向量机: 最小化hinge损失

Loss Function

损失函数是一种评估“你的算法/模型对你的数据集预估情况的好坏”的方法。如果你的预测是完全错误的,你的损失函数将输出一个更高的数字。如果预估的很好,它将输出一个较低的数字。当调整算法以尝试改进模型时,损失函数将能反应模型是否在改进。“损失”有助于我们了解预测值与实际值之间的差异。损失函数可以总结为3大类,回归,二分类和多分类。
常用损失函数:
Mean Error (ME)
Mean Squared Error (MSE)
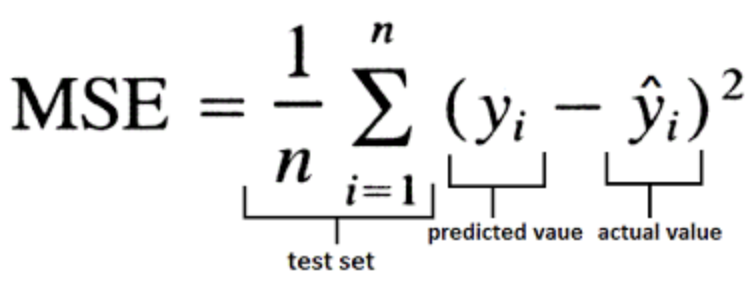
Mean Absolute Error (MAE)
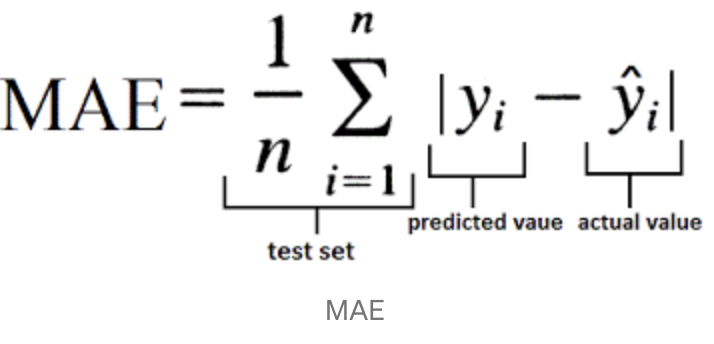
Root Mean Squared Error (RMSE)
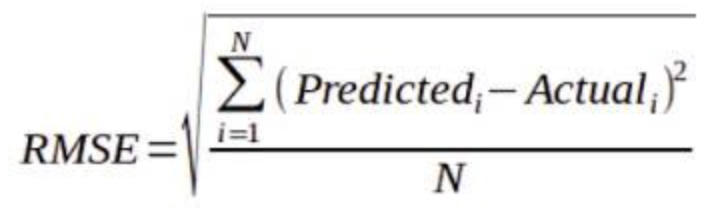
Categorical Cross Entropy Cost Function(在只有一个结果是正确的分类问题中使用分类交叉熵)
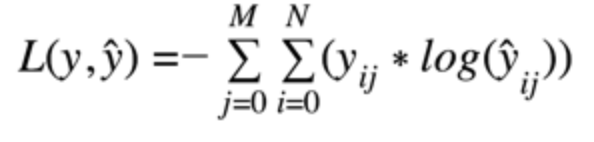
Binary Cross Entropy Cost Function.
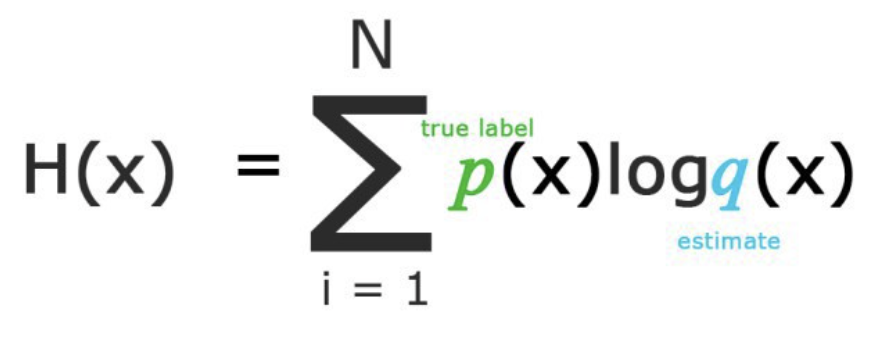
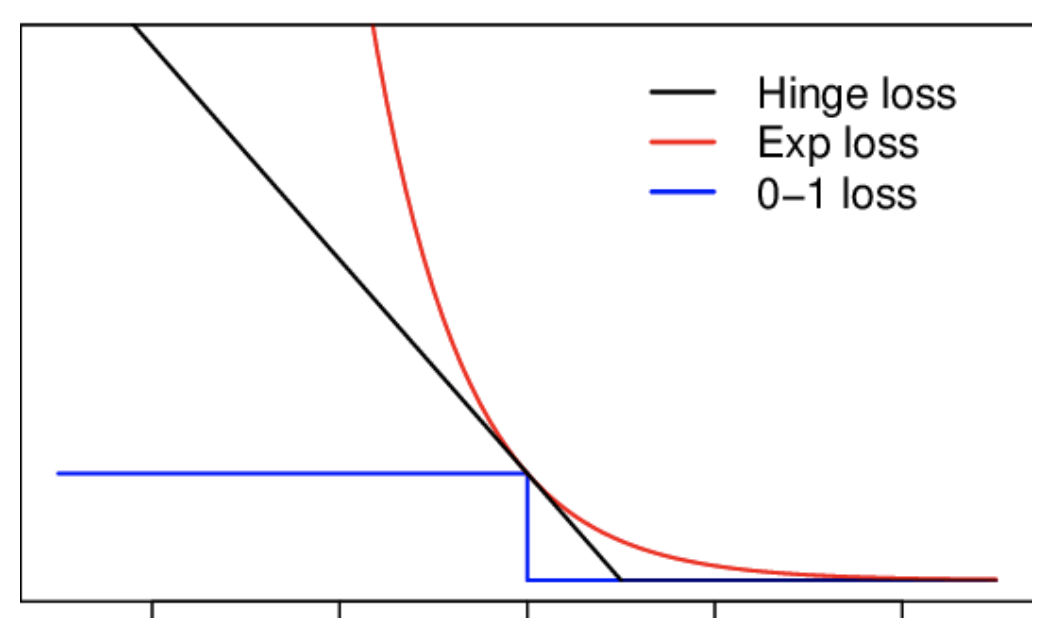
Hinge Loss(hinge损失不仅会惩罚错误的预测,也会惩罚那些正确预测但是置信度低的样本)
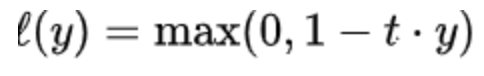
Multi-class Cross Entropy Loss
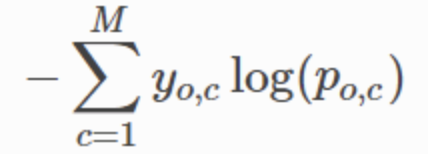
这里我们要区分Multi-class和Multi-label,如下图:
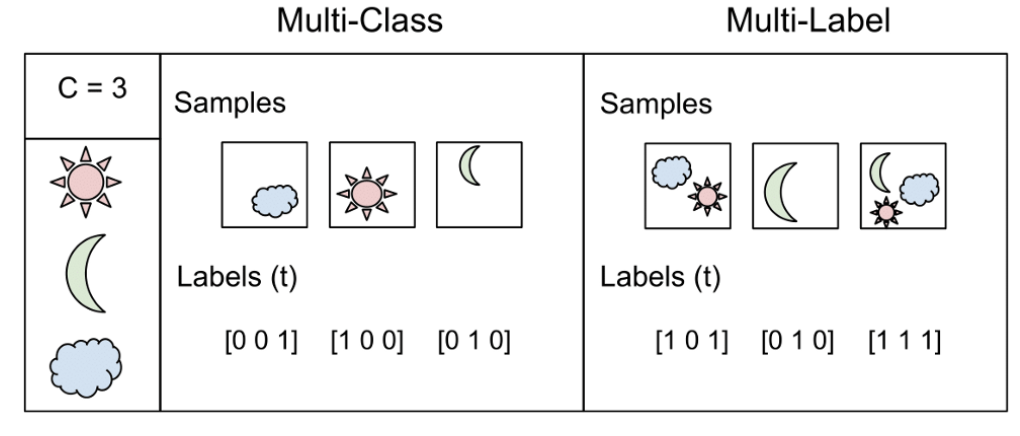
对于Multi-Label我们不能使用softmax,因为softmax总是只强制一个类变为1,其他类变为0。因此,我们可以简单地在所有输出节点值上用sigmoid,预测每个类的概率。
Divergence LOSS (KL-Divergence)
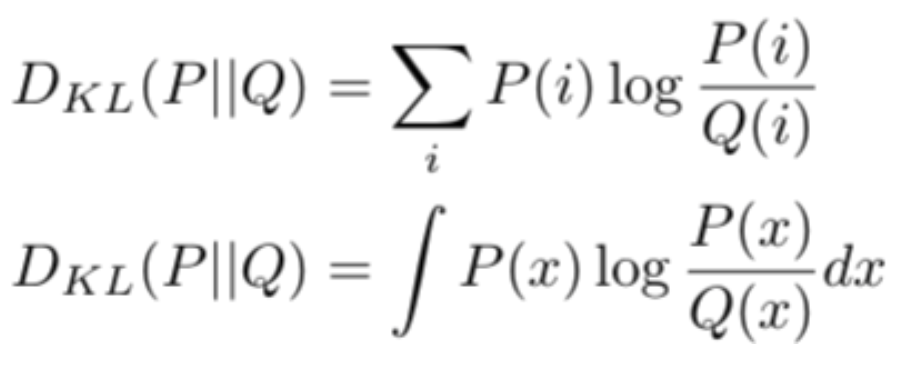
KL散度是一个分布与另一个分布的概率差异的度量,KL散度在功能上类似于多类交叉熵,KL散度不能用于距离函数,因为它不是对称的。
Huber loss
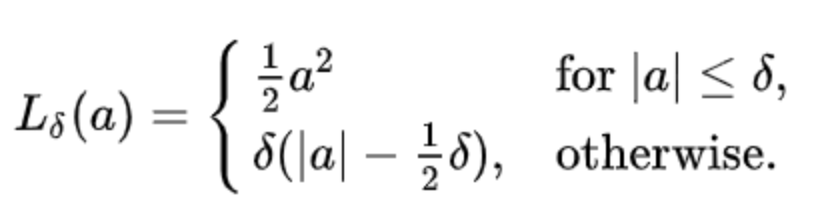
a为比较小的值,此函数是二次函数;对于a为大值时,此函数是线性函数。变量a通常是指残差,即观测值和预测值之间的差值。与平方误差损失相比,Huber损失对数据中的异常值不那么敏感。使函数二次化的小误差值是多少取决于“超参数”,𝛿(delta),它可以调整。
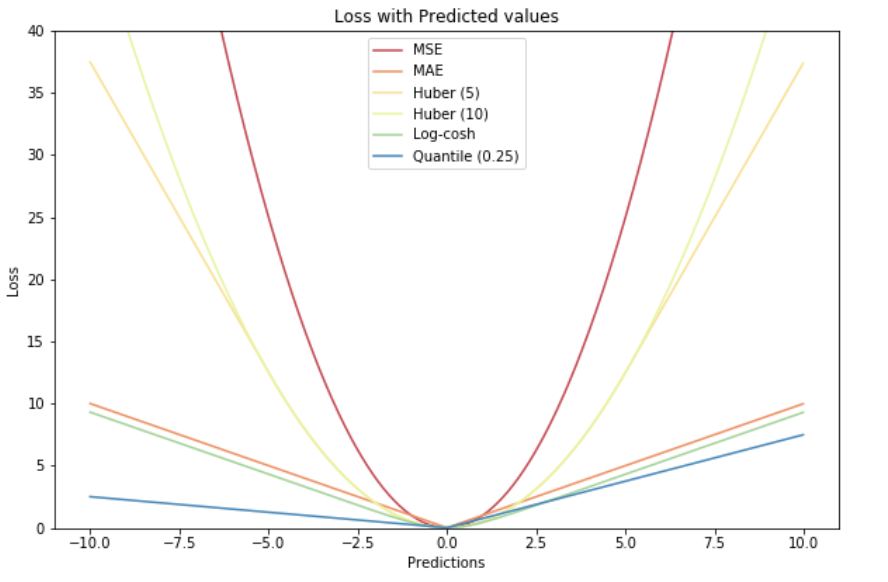
有的时候,我们的任务并不是回归或分类,而是排序,下面介绍rank loss。

Rank Loss

排名损失用于不同的领域,任务和神经网络设置,如Siamese Nets或Triplet Nets。这就是为什么他们会有名称,如Contrastive Loss, Margin Loss, Hinge Loss or Triplet Loss。
与其他损失函数(如交叉熵损失或均方误差损失)不同,损失函数的目标是学习直接预测给定输入的一个标签、一个值或一组或多个值,rank loss的目标是预测输入之间的相对距离。这个任务通常被称为度量学习。
rank loss在训练数据方面非常灵活:我们只需要得到数据点之间的相似性得分就可以使用它们。分数可以是二元的(相似/不同)。例如,假设一个人脸验证数据集,我们知道哪些人脸图像属于同一个人(相似),哪些不属于(不同)。利用rank loss,我们可以训练CNN来推断两张人脸图像是否属于同一个人。
为了使用rank loss,我们首先从两个(或三个)输入数据点中提取特征,并得到每个特征点的嵌入表示。然后,我们定义一个度量函数来度量这些表示之间的相似性,例如欧几里德距离。最后,我们训练特征提取器在输入相似的情况下为两个输入产生相似的表示,或者在两个输入不同的情况下为两个输入产生距离表示。
Pairwise Ranking Loss
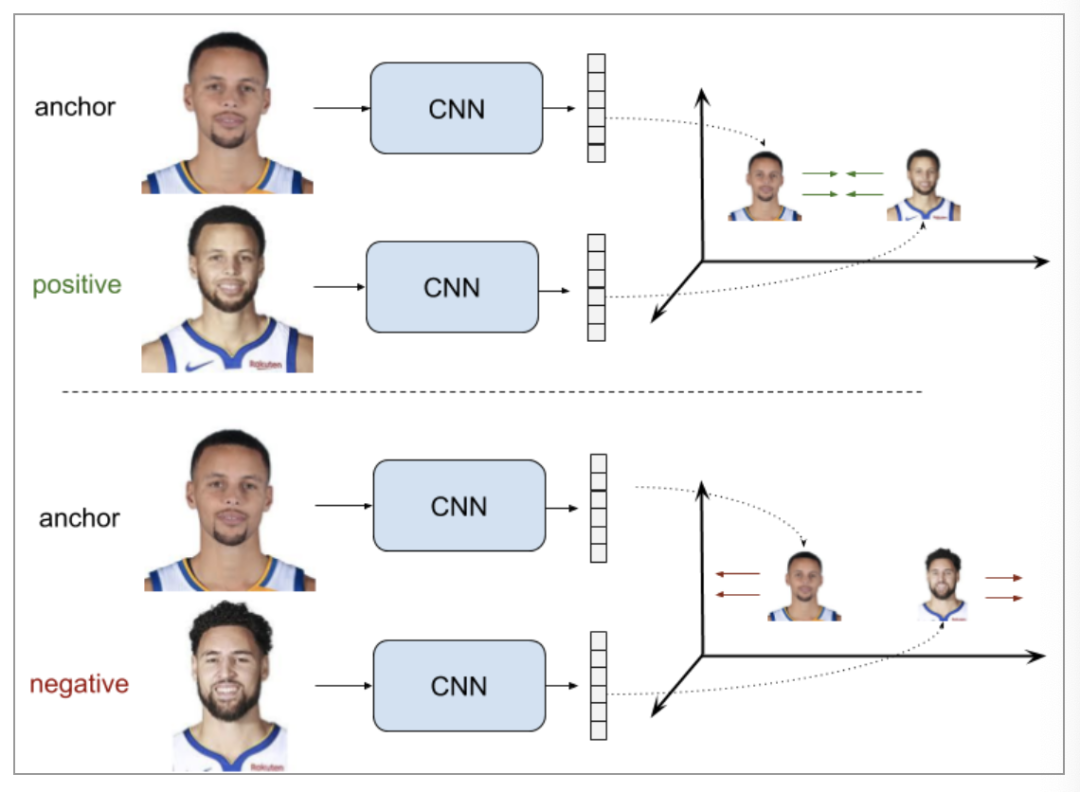
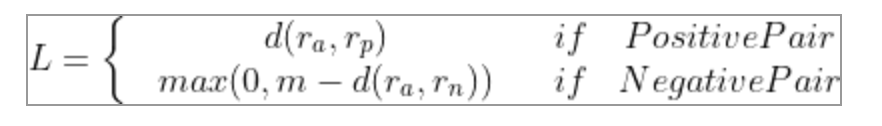
我们从上式可以看到,当两个人的描述的是一个人时,他们嵌入表示距离大小就是loss,当描述不是一个人时,嵌入表示距离大于margin才不会产生loss。我们也可以把公式改写为:
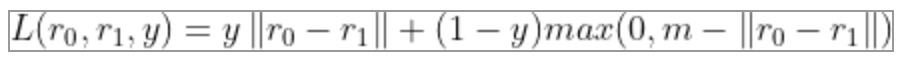
Triplet Ranking Loss
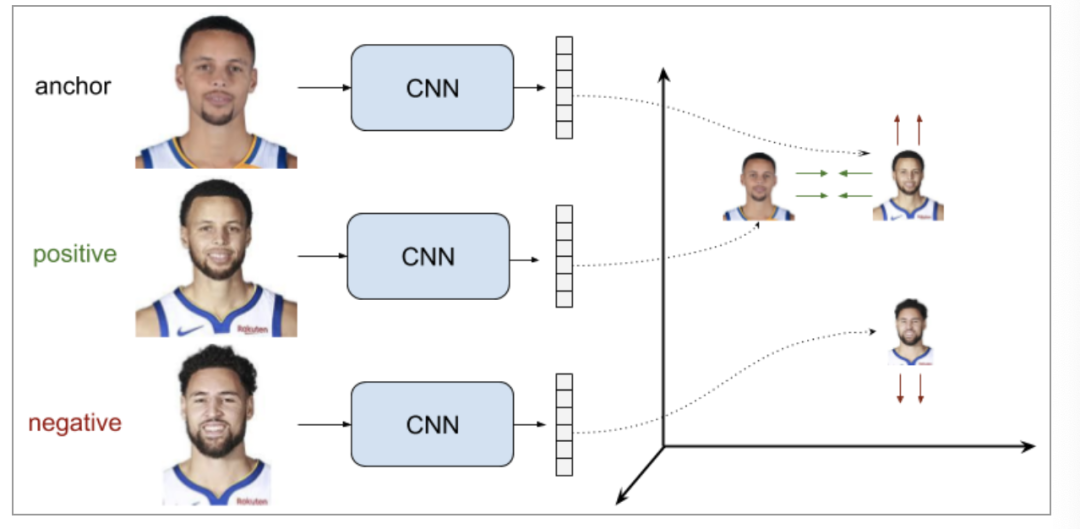
通过使用三组训练数据样本(而不是成对样本),这种设置优于前者(同时优化类内距离和类间距),目标就是使得锚点与负样本距离显著大于(由margin决定)与正样本的距离,loss定义如下。
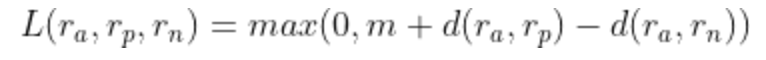
我们来分析一下这种损失的三种情况:
Easy Triplets: 相对于嵌入空间中的正样本,负样本已经足够远离锚定样本。损失是0并且网络参数不会更新。
Hard Triplets: 负样本比正样本更接近锚点,损失是正的。
Semi-Hard Triplets:负样本比正样本离锚的距离远,但距离不大于margin,所以损失仍然是正的。
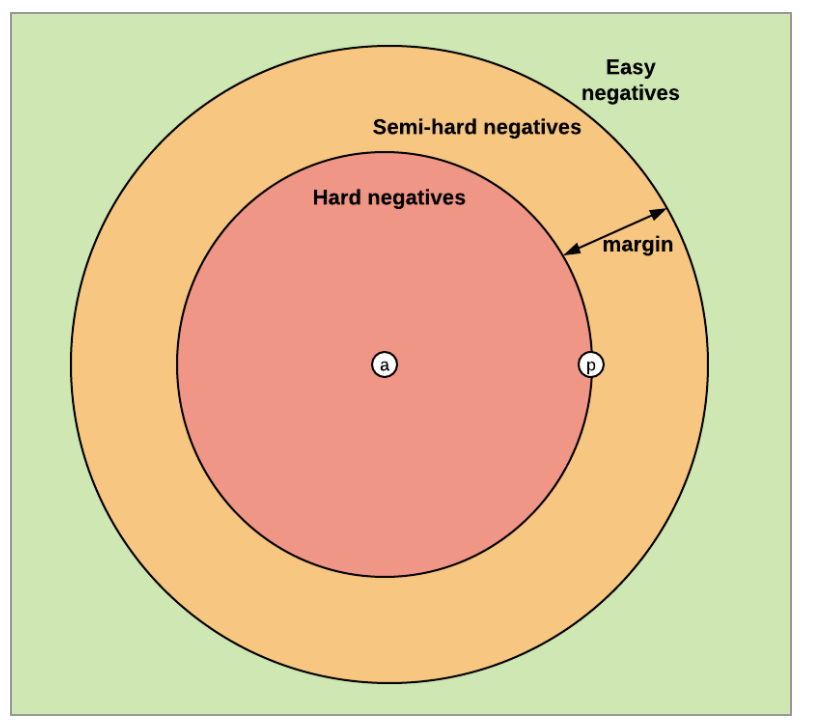
负样本选择:
在triplets loss训练过程中,负样本选择和三元祖样本挖掘是非常重要的。选择的策略对训练的效率和最终效果有很大的影响。一个很重要的点是,训练三元祖应避免easy triplets,因为他们所造产生的loss是0,不能用于优化模型。
样本挖掘的第一种策略离线进行三元组挖掘,这意味着三元组是在训练开始时定义的,或者是在每个epoch前。后来又提出了online triplet loss(在线三元组挖掘),即在训练过程中为每一个epoch定义三元组,从而提高了训练效率和性能。
需要注意的是,选择负样本的最佳方法是高度依赖于任务的。

Circle loss

在理解了triplet loss之后,我们终于可以开始研究circle loss:A Unified Perspective of Pair Similarity Optimization。Circle Loss 获得了更灵活的优化途径及更明确的收敛目标,从而提高所学特征的鉴别能力。它使用同一个公式,在两种基本学习范式,三项特征学习任务(人脸识别,行人再识别,细粒度图像检索),十个数据集上取得了极具竞争力的表现。
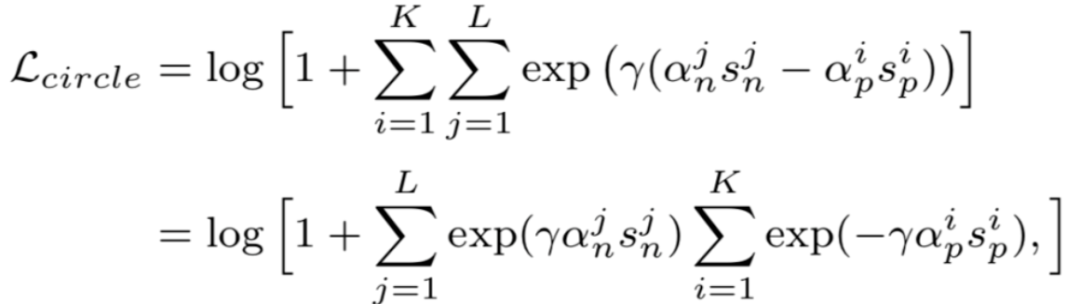
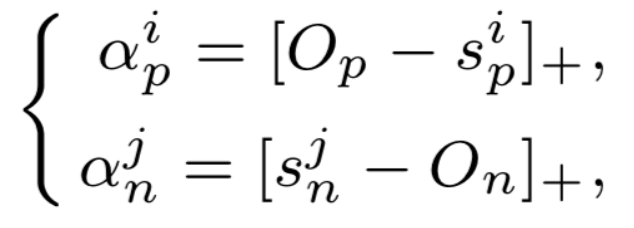
✄------------------------------------------------
双一流高校研究生团队创建,专注于计算机视觉原创并分享相关知识☞
闻道有先后,术业有专攻,如是而已╮(╯_╰)╭
