1500字,8个问题,彻底理解堆!

堆(heap)是计算机科学中被广泛使用的数据结构,如排序、推荐,还可作为优先级队列,与图也能结合,还能与常见算法思想如贪心等结合起来,高效实现算法。
要想掌握堆,可能需要首先考虑清楚以下几个问题:
什么是堆? 数组和堆的关系? 已知数组,如何构建一个小根堆 构建堆的时间复杂度是多少? 堆的应用都有哪些? 删除最小元素,如何再构建堆? 向建好的堆中,插入一个元素,如何再构建堆? 使用堆的案例:最后一块石头的重量
下面,我尽量用最精简的语言解释上述问题,若有错误或表达不清楚地方,请留言告诉我。
1 什么是堆?
个元素的序列,当且仅当满足下关系时,称之为小根堆:
其中,
2 数组和堆的关系?
物理存储上,堆一种完全基于数组的数据结构;逻辑存储上,堆又是一颗完全二叉树。太强了!
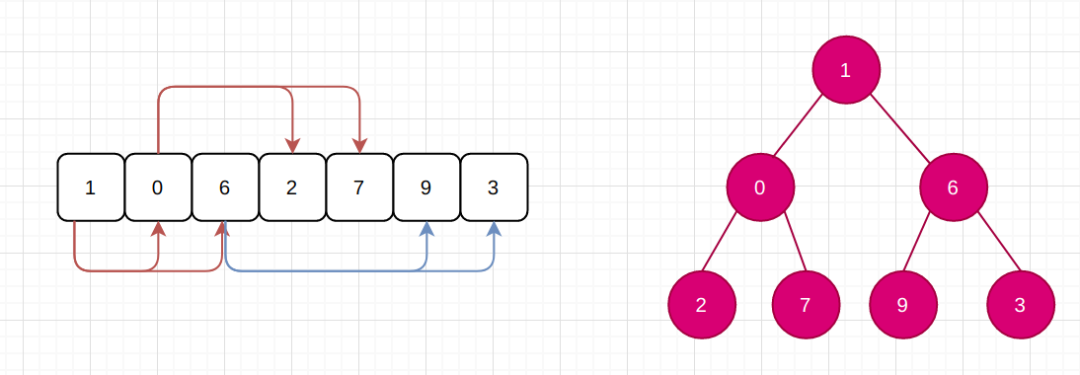
3 已知数组,如何构建一个小根堆?
这个问题,完全可以当作一道编程题,实际确实也是面试中最高频题目之一。构建小根堆,形象来说,就是不断调整三角的过程:
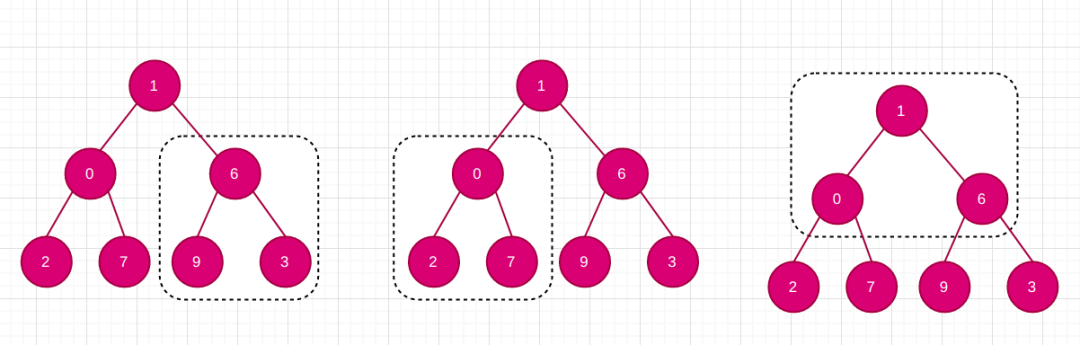
数组折半处才可能有左、右子节点,每次从上、左、右角点中选择最小者,并调整到上角点中。并依次调整这样的三角。
了解以上过程,要想一次写出无任何bug的建堆代码,依然充满挑战。确实太容易出错了!
#! ~/anaconda3/bin/python3.7
def heapify(nums):
"""
build a minimize heap
:type nums: list
:param nums: input list
:return: minHeap
"""
for low in range(len(nums)//2, -1, -1):
down_adjust(nums, low, len(nums))
def down_adjust(nums, low, high):
"""
heapify at [low,high]
:param nums: list
:param low:
:param high:
:return:
"""
parent = low
left = 2*parent + 1
while parent < high:
if left+1 < high and nums[left+1] < nums[left]:
left = left + 1
if left < high and nums[left] < nums[parent]:
nums[left], nums[parent] = nums[parent], nums[left]
parent = left
left = 2*parent + 1
else:
break
这个代码测试多遍,目前未发现bug.
4 构建堆的时间复杂度是多少?
留意heapify 函数,这层循环是线性次数,down_adjust函数,每循环一次, parent 都会乘以2,因此循环次数为 .
综合时间复杂度为:,其中为数组长度。
5 堆的应用都有哪些?
我们熟知的堆排序正是基于堆,它是一种排序快且稳定的排序算法,Python解释器的排序函数基于它,进一步验证它的高效。
基于堆能实现优先级队列,就于小根堆而言,根节点是最小值,移除最小值再建堆的时间复杂为,性能佳。
用最小堆结构还可以实现一个特殊的树结构–哈弗曼树(Haffman Tree)。哈弗曼树可以用来给文本压缩、也可以解决一些优化问题。
对于推荐算法中,推荐最热商品TOPK问题,堆都会有一定使用。
6 删除最小元素,如何再构建堆?
上面说到,移除小根堆的最小元素后,依然要维持堆的结构。一般做法:堆的最后一个元素覆盖第一个元素,再次调用down_adjust函数调整:
def heap_pop(nums):
"""
:param nums: heap
:return: heap after removing minimize elements
"""
nums[0] = nums[-1]
down_adjust(nums, 0, len(nums))
nums.pop()
因为down_adjust函数时间复杂度为,所以删除最小元素构建堆的时间复杂度为.
7 插入一个元素,如何再构建堆?
这个过程一般操作方法:插入到堆的最后,然后与对应父节点比较大小,不断向上调整。
这个代码,大家不妨自己写一下,不超过10行。顺便测验下你是否真正理解堆。
8 使用堆的案例:最后一块石头的重量
这是一道leetcode的题目。题目是这样:
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出两块 最重的 石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。最后,最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下,就返回 0。
看懂题意了吗?看不懂的点击:https://leetcode-cn.com/problems/last-stone-weight
分析
直接根据题目的要求,选出当前最大两块石头,消除一下,显然这个操作与后续状态无关,因此贪心求解即可。
使用堆数据结构,因为Python中默认的heapq为小根堆,简单转换一下。时间复杂度为O(n),空间复杂度为O(n)
代码
from heapq import *
class Solution(object):
def lastStoneWeight(self, stones):
"""
:type stones: List[int]
:rtype: int
"""
stones = [stone*-1 for stone in stones]
heapify(stones)
while len(stones) > 1:
fst,sec = heappop(stones),heappop(stones)
if fst - sec < 0:
heappush(stones,fst-sec)
return -heappop(stones) if stones else 0
使用堆非常方便的返回前K个最值,压入元素依然会维护堆结构。
以上就是今天堆heap的总结,如果对你有帮助,不妨给我点赞支持下,让我更有动力写好一篇,谢谢。
今天送3本书,大牛周志华老师的《集成学习:基础与算法》

送书方法:从留言被点赞10次及以上中的选择。点击下方链接,了解此书详情:
