Apple官网源码中使用transform:matrix(),这是什么?
开篇
01
向量与矩阵基础知识
关于这部分内容,有线性代数基础的同学们可以忽略本部分内容,在这里笔者只会介绍最基础的内容,主要涉及什么是向量和矩阵,以及对应的基础运算。
向量
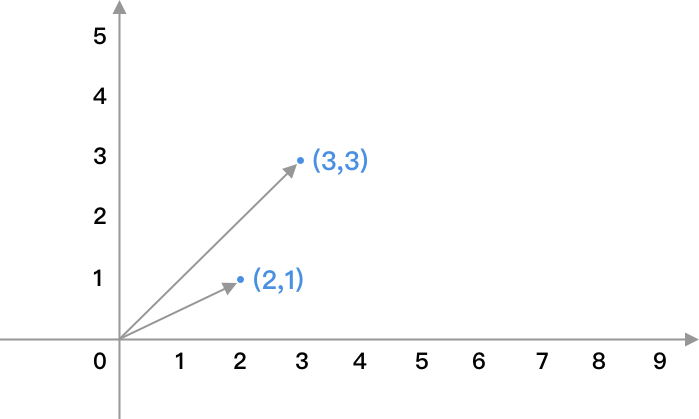
向量被用于许多科学领域用来描述方向和大小,我们一般用笛卡尔坐标系进行向量的描述,向量简单的来说就是把数排成一列或一行进行展示,比如向量(2,1)和(3,3)在坐标系中表示如下:
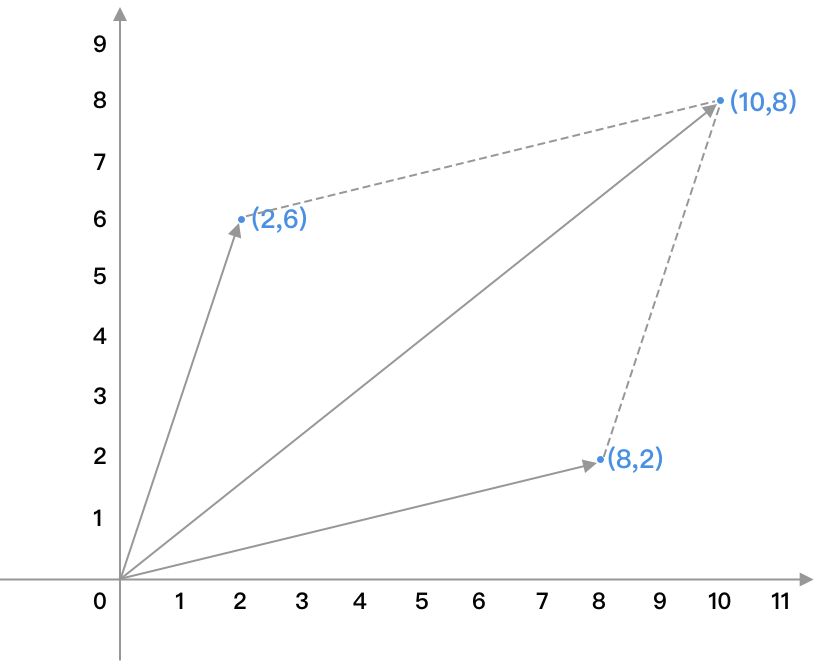
假设我们现在有两个向量AB(8,2)和向量AC(2,6),我们对其进行加、减、乘运算,示例如下:
向量加法:
AB+AC=AD
(8,2)+(2,6)=(8+2,2+6)=(10,8)
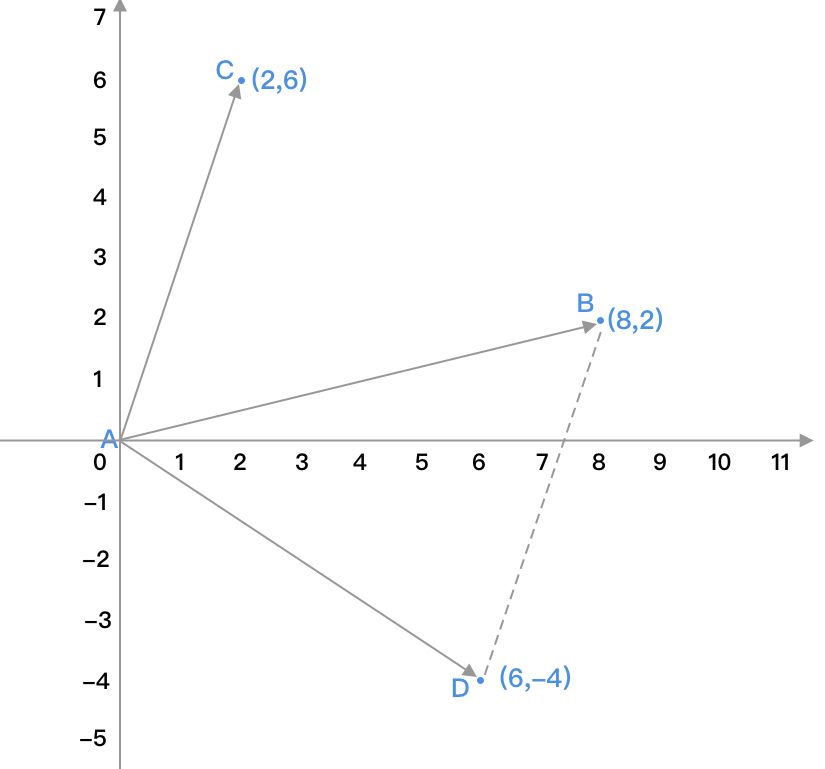
向量减法:
AB-AC= AD
(8,2)-(2,6)=(8-2,2-6)=(6,-4)
向量乘法:
AB✖️AC = AD
(8,2)✖️(2,6)=(8✖️2,2✖️6)=(16,12)
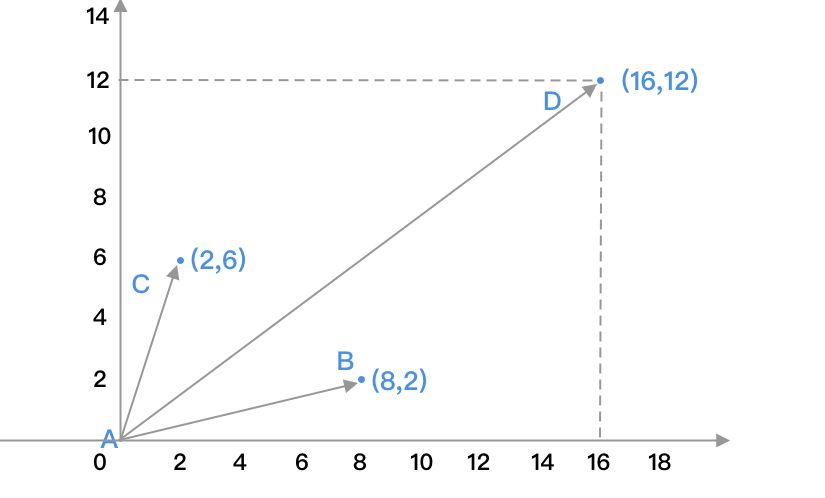
从上述例子我们可以看出,向量的运算即为每个向量对应的位置进行两两相加、两两相减或两两相乘。
矩阵
简单来说把数排列成长方形就是矩阵,我们一般用几行几列来描述矩阵,比如 2✖️2 矩阵,2✖️3 矩阵等,乘号左边代表行数,乘号右边代表列数,如下图所示表示2✖️2 的矩阵:
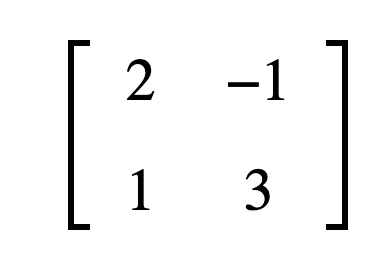
矩阵相加:
相同规模(行数列数都相等)的矩阵之间的加法如下图所示:
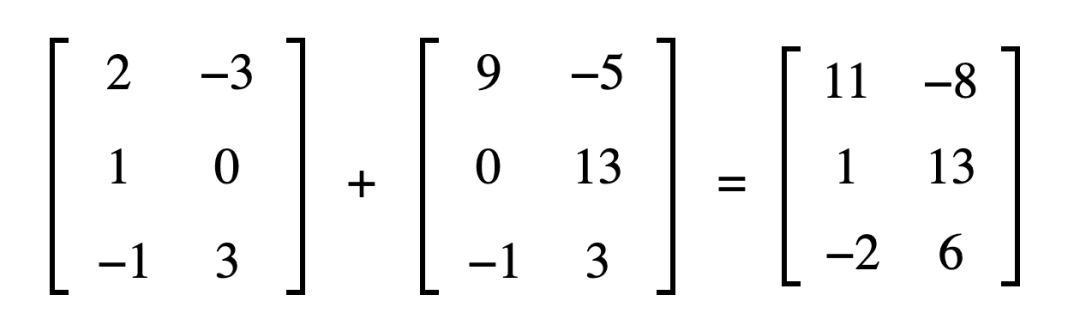
我们可以看出是对应的位置两两相加而得。
矩阵相乘
1、矩阵与向量相乘,示意图如下:
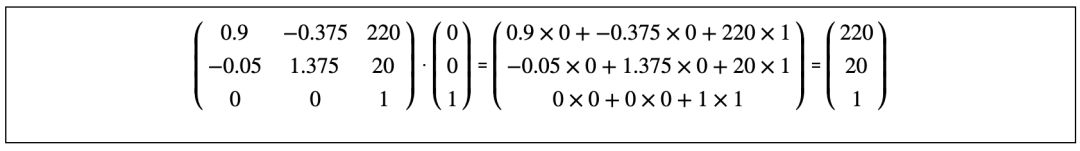
从图可以看出矩阵与向量相乘结果为向量,矩阵每行的数字分别与向量每行对应的位置分别相乘最后将结果相加,得到结果向量。
2、矩阵与矩阵相乘
比如 2✖️4 的矩阵与 4️✖️3 的矩阵相乘我们得到一个 2✖️3 的矩阵,如下图所示:
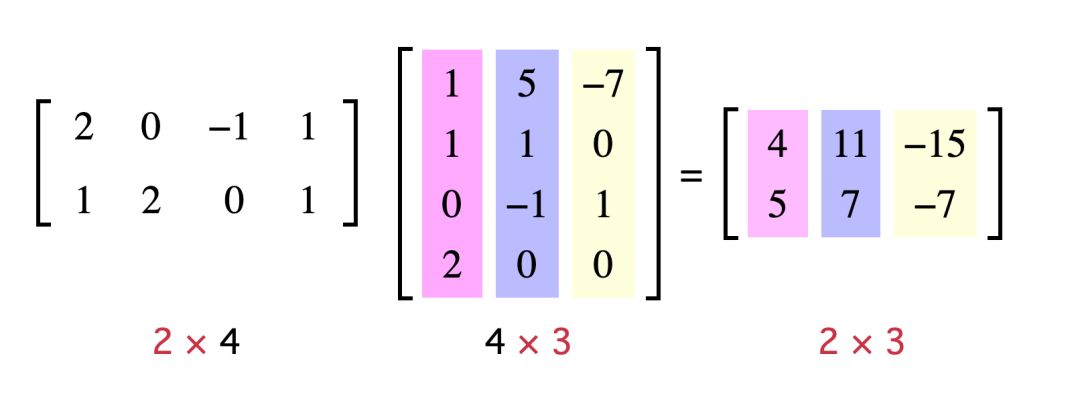
从图示中我们可以看出,我们左边矩阵的每行与右边矩阵的每列分别相乘,相乘规则如矩阵与向量相乘的规则一样,最终得到矩阵的行数等于左边矩阵的行数,列数等于右边矩阵的列数。
02
一个matrix()的例子
介绍完基本向量和矩阵的知识后,我们来看看一个matrix()的例子,transform:matrix(a,b,c,d,ex,fy)一共六个参数,用矩阵表示如下图所示:

注:参数书写的方向是竖着写的。
这六个参数代表什么意思,这里先不做介绍,稍后会详细介绍,现在我们有这样一个元素,其对应的CSS属性如下:
#transformedObject {
position: absolute;
left: 0px;
top: 0px;
width: 200px;
height: 80px;
}
此段代码,对应的页面效果如下:
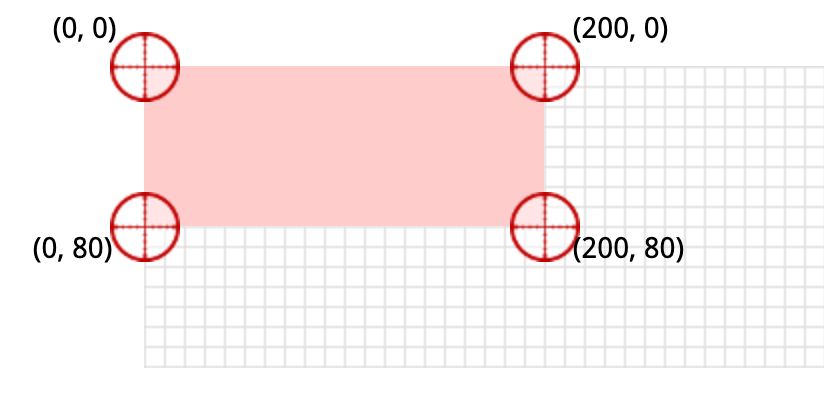
从上图我们可以看出,此长方形的四个顶点从左顶点开始,顺时针方向对应的坐标分别为:(0,0)、(200,0)、(200,80)、(0,80),我们对其进行transform:matrix(0.9, -0.05, -0.375, 1.375, 220, 20)变换,css代码如下:
#transformedObject {
position: absolute;
left: 0px;
top: 0px;
width: 200px;
height: 80px;
transform: matrix(0.9, -0.05, -0.375, 1.375, 220, 20);
transform-origin: 0 0;
}
注:transform-origin是变形原点,也就是该元素围绕着那个点变形或旋转,该属性只有在设置了transform-origin属性的时候起作用。
应用这个属性后的效果如下图:
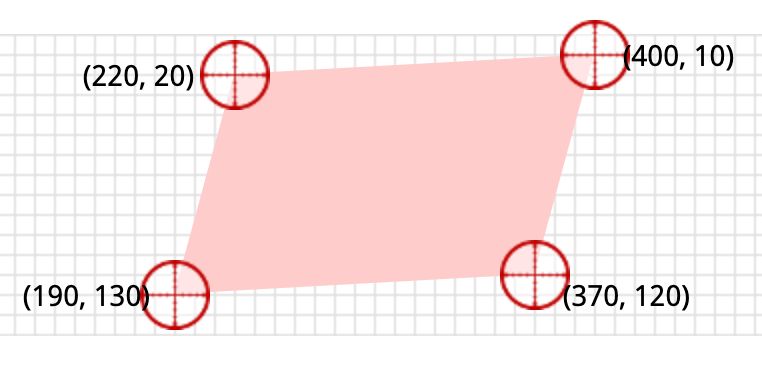
好奇的你,你一定困惑这四个点的值是怎么得出来的呢,其实有了前面的向量和矩阵知识,我们很容易算出,matrix(0.9, -0.05, -0.375, 1.375, 220, 20)用矩阵表示如下图所示:
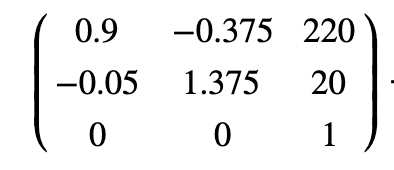
元素最初的每个顶点相当一个向量,例如(200,0)可用下图表示:
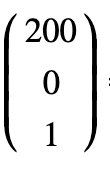
变换后的四个点的坐标值,其实是matrix(0.9, -0.05, -0.375, 1.375, 220, 20)对应的矩阵与原始四个点对应的向量分别相乘而得,具体的运算过程如下图:
与(200, 80)相乘的运算过程得到点(370,120):

与(200, 0)相乘的运算过程得到点(400,10):
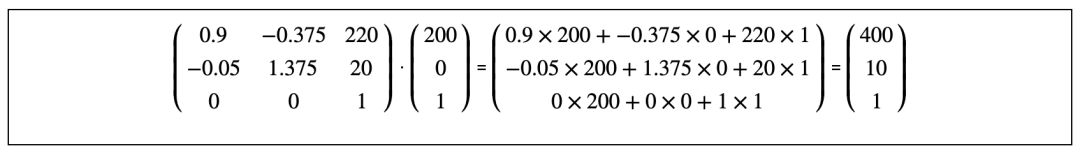
与(0, 80)相乘的运算过程得到点(190,130):
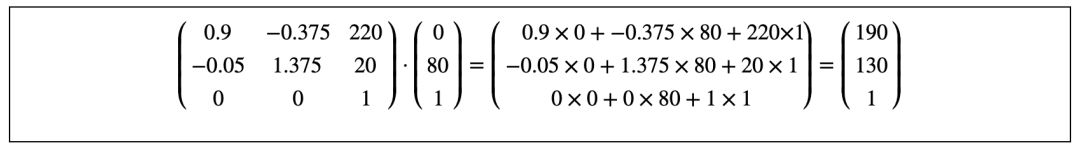
与(0,0)相乘的运算过程得到点(220,20):
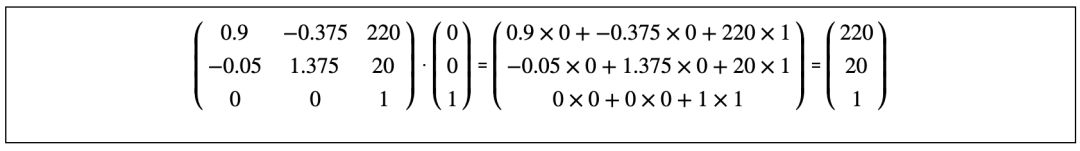
经过运算后,我们得到最终变换后的四个顶点坐标: (220,20),(400,10),(370,120),(190,130)
03
matrix参数详细介绍
通过前面的学习,我们学到了向量和矩阵的基础知识,一个matrix()变换的例子,我们通过矩阵运算算出了变换后的结果。接下来我们一起学习下transform:matrix(a,b,c,d,tx,ty)这六个参数代表的意义,其实这六个参数,对应的是translate(x,y),scale(x,y),rotate(angle),skew(x-angle,y-angle)这些效果,每种变换效果对应的参数不同,如下图总结:
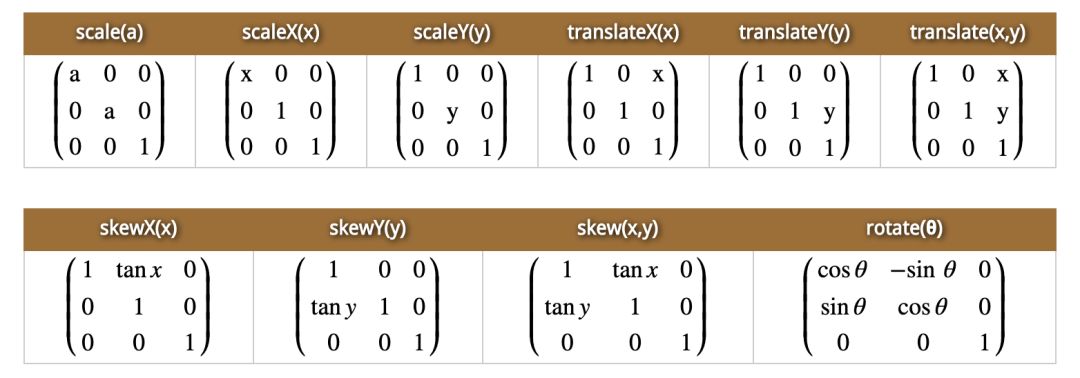
现在有这个需求,我们对元素进行顺时针旋转15度,X轴方向右移230px, X轴方向扩大1.5倍,我们使用基本的变换属性代码如下:
#o1 {
transform-origin: 0px 0px;
transform: rotate(15deg) translateX(230px) scaleX(1.5);
}
如果用transform:matrix()怎么实现如上的相同效果呢,其实我们可以利用transform:matrix(a,b,c,d,tx,ty)这六个参数对应的总结(如上图),其实就是每种变换对应的矩阵参数相乘的结果得到这6个参数值,记住一定要按照rotate,translateX,scaleX对应的顺序进行举行相乘(矩阵相乘顺序不同结果不同),如下图所示:(运算的结果笔者就不写了,留给大家练习下矩阵相乘)

今天的内容就介绍到这里,我们理解了transform这个高级属性——matrix()矩阵属性,通过这个属性我们了解其背后的数学逻辑,只有理解掌握这个属性后,我们才能实现更为复杂的动画效果。

点击上方卡片,关注一下~