干货 | 数据结构与算法 - 什么是算法
文案 向柯玮
排版 邓发珩
疫情尚未结束，今天继续加油！在家好好学习，好好充实自己，祝大家身体健康。
前言
大家好呀， 我是小玮~今天给大家带来的是学习笔记之数据结构与算法--什么是算法。
说到算法呀，我相信每个学过编程的人都或多或少接触到过。但是可能呢，你并不了解一个算法的定义是什么，算法好坏如何判断，算法和数据结构的关系，等等。让我们带着我们的疑问，慢慢地去走进算法，去了解它。
本次学习笔记的主要内容有：数据结构和算法的关系，算法的定义，算法的特性，算法设计的要求，算法效率的度量方法，时间复杂度与空间复杂度。
数据结构与算法
其实现在市面上关于数据结构的书的名字，一般都不是单单以数据结构为名，它通常是以数据结构与算法为名，比如怎么学好数据结构与算法。其实在算法导论中，也是把数据结构和算法一块讲的。
那么为什么他们总是在一块呢？我们可以举一个例子来说。你把房子的基础打好了，但是你没有想好上面应该怎么修，那房子还修不修？同理，你把上面怎么修想好了，基础却不知道怎么办，那房子还修不修？
再举一个例子，你要去看话剧，发现话剧名字叫做《罗密欧》，很奇怪，就去问前台这是怎么回事，前台解释说，女主角生病了，演不了了，只有男主角了，所以这部话剧改为讲男主角的心路历程。那话剧还看得下去吗？
没错，数据结构和算法的关系也是类似，只学数据结构，你会感觉自己什么都没有学到，只学算法，你会总感觉不能很完整。
算法的定义
其实算法就是描述解决问题的方法，它最早是花拉子米提出来的，没错就是咱们数学书上面的花拉子米。从中可以看出，编程果然是与数学有着密不可分的关系啊。
在现代，最普遍认可的算法的定义是：算法是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。其实这个也很好理解，就是为了解决某个问题，把一些指令按照顺序排起来，完成一些操作，这就是算法。
算法的特性
说到算法的特征，一般来说公认的有五大基本特征，即：输入，输出，有穷性，确定性和可行性。
输入：这个其实相对来说很容易理解，一个算法可以有零个或者多个输入，比如说，我们第一次学编程的时候，我们做的第一个算法是什么？没错，就是输出‘hello world’，这个就不需要咱们输入参数，但是绝大多数算法都是需要我们输入一些参数进去的。
输出：一个算法最起码会有一个或者多个输出，如果你的算法没有输出，你设计它干什么呢？
有穷性：它在严格意义上来讲，并不仅仅是数学意义上无穷的对立，它是指程序在人们可以接受的时间范围内完成，如果一个程序陷入了无限循环，或者一个算法需要运算几十年，那都算无穷，那都是没有意义的算法。
确定性：这个也非常容易理解，算法的每一个步骤都具有确定的意义，不会出现多重含义，算法在一定的条件下，只能有一条执行路径。一旦出现了歧义，那么编译器就会报错，我相信这一点大家都理解吧？
可行性：算法的每一步都必须是可执行的，也就是说，每一步都能够通过执行有限次数完成。这一点，我感觉有有穷性有异曲同工之处。
算法设计的要求
我们都知道，想要实现某种目的，我们可以设计多种多样的算法去实现，但是一个好的算法，他一般都满足以下的特点。
正确性：它的意思是，算法至少应该具有输入,输出和加工处理无歧义，能正确反映问题的需求，能够得到问题的正确答案。它主要包括四个层次：1、没有语法错误。2、对于合法的输入，能够给出满足要求的输出。3、对于错误的输入，能够给出相应规格提示的输出。4、对于各种刁难的输入，也能给出满足要求的输出。
可读性：它的意思是，算法设计的另一目的是为了便于阅读，理解和交流。对于一个优秀的算法而言，它不仅仅要求是解决这个问题，它还要求别人能够理解，这样也有利于算法问题的发现以及改进，同时更是方便自己以后回来再看的时候能够明白。
在这里我想到了一个例子，前段时间有很多有用最少代码完成xxx的挑战，很多大神确实用了很少很少的代码，完成了这些挑战，但是代码最终公布出来，很少人能够明白其中的意思，这样的代码就不属于好的代码。
健壮性：它的意思是，能够对错误的数据进行正确的相应处理，而不是输出一些稀奇古怪的东西。举个例子来说，你设计了一款根据路程求时间的算法，他们输入了一个负数进来，你的算法应该能够给出相应的回复，而不是异常的回复。
时间效率高并且储存量低：这个其实就是评判算法好坏最关键的一点，也是从事优化算法行业的人最高的追求。就和人们在现实生活中一样，我们总是想用最少的投入，获得最大的收益。那么一款优质的算法也是一样，它讲究用最快的时间，最少的空间，去完成最多的任务。
算法效率的度量方法
对于一个算法的效率，我们应该怎么度量呢？它主要分为两种：事后统计方法和事前分析估算方法。
事后统计方法：这种方法主要是通过设计好程序以后的测试程序和数据，利用计算器对不同算法编制的程序的运行时间进行比较，从而判断算法的效率。这种方法的缺陷很明显。我觉得主要有以下几点：
>有可能导致花费了大量时间去写一个程序，最后运行了发现是一个很糟心的程序 。
>比较的方式有误，运行时间不仅仅是取决于算法的好坏，同时也取决于电脑配置的好坏，你用同样的算法在最先一代电脑上运行和在现在最旗舰的电脑上运行，效果肯定存在巨大差异。
>测试数据存在选择问题，你不知道自己的算法应该选取多大的数据，就那排序算法来说，几个数字的排序，无论哪一种算法，其实都差不多，只有当数据非常大的时候才会有明显差异。
事前估算分析方法：它的意思是，在编译之前，就依据统计方法对算法进行估算。那么这个估算主要是在哪些方面呢？
>算法采用的策略，方法。
>编译产生的代码质量。
>问题的输入规模。
>机器执行指令的速度。
第一条当然是算法好坏的根本，第二条是由编译器决定的，第四条需要看电脑的性能，也就是说，不考虑软件和硬件，一个程序的运行时间其实是取决于算法的好坏和问题的输入规模（即输入量的多少）。
下面我们举一个例子来说明一下。等差数列求和，大家肯定都知道吧？那么针对这个问题，我们可以设计两种最常规的算法。
1:cin>>n;int i,sum=0;for(i=1;i<=n;i++)sum+=i;cout<2:cin>>n;int sum=0;sum=(1+n)*n/2cout<
在这两种算法中，虽然我们输入的是一样的，但是内部的计算过程是完全不在一个等级的，这就是1与n的差距。对吧？
我们在分析程序时间的时候，就应该把程序当成是独立于程序语言一系列步骤，我们把其中的基本操作的数量和输入规模联系起来。
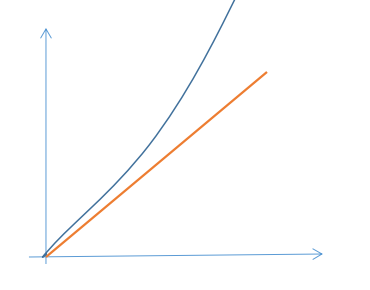
就拿上面的例子来说，对于同样的输入规模n，方法一需要运n^2次，而方法二只需要运行n次。这就是一个质的飞跃。
时间复杂度与空间复杂度
说到这两个概念，虽然在书上看到很多相关的内容但是我觉得我们只需要关注两个方面，即：它们的意思是什么，它们怎么推导。
时间复杂度：我们通常用O（x）来表示时间复杂度，它的意思是在最坏的条件下，这个程序会运行多少次。打个比方来说，我们现在用冒泡排序对面下面的数组进行排序。
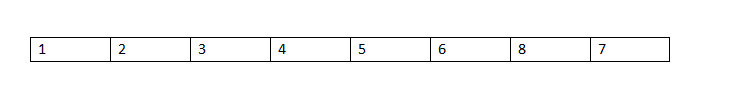我们只需要运行一次就可以完成我们的目的，但是如果是下面这个数组呢？
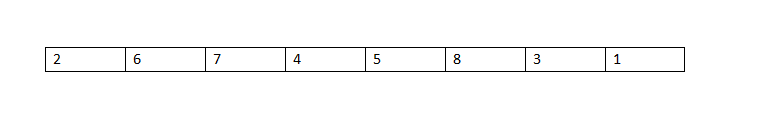是不是相应的，程序运行次数就更复杂了？那么最坏的情况是什么样的呢？
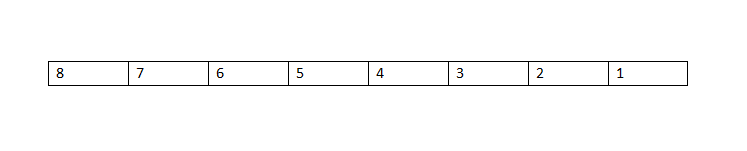没错，就是这种情况，那么这种情况下，程序会运行多少次？是8^2=64次吧？那么依据我们的定义，冒泡排序的时间复杂度就是O（n^2）。我们通常将推导时间复杂度的过程叫做，推导大O阶，那么就可以知道，我们把上面出现的n^2，称为平方阶，把n称为线性阶，那么，现在我们来思考一下，如果是lg(n)呢？没错，就是对数阶了。
在推导的过程当中，我们应该注意的是：
>如果这个n为一个常数，我们统一认为时间复杂度是O(1)。
>如果n的前面存在系数，我们统一认为时间复杂度是O(n)，即把前面的系数当成1处理。
>如果最终算出时间复杂度为O(n^2+n-i)的类似形式，我们只保留最高阶。
空间复杂度 ：既然已经有了时间复杂度的基础，那么空间复杂度也就不难理解了。而且如果出现了复杂度，在通常情况下，都是指的时间复杂度。
我在这里就不多加介绍空间复杂度了。我们直接写出空间复杂度的表示方法。S(n)=O（f（n）），这里n是问题的规模，f（n）是关于n所占储存空间的函数。
到这个位置为止，我们基本上已经完全了解了数据结构和算法的一些基本内容。在之后的推文中，我们就正式进入数据结构与算法的主体内容了。
希望各位看客老爷能够认真地读好前两篇推文，这是一个非常重要的基础部分。那么，我们下期再见啦~
评论