聊聊我的一次真实 Python 面试经历

作者:SyntaxError
出处:segmentfault.com/a/1190000022455160
首先我挺喜欢这家公司的面试风格的,也是比较务实的吧。无奈自己的心理因素和技术水平都不好,导致面试失败。再接再厉吧
1.一上来就是编程题三连
1.1 大概意思就是:俩列表a b,如果a中的元素在b中,那么就保存此元素在a中的索引值,最后统一输出所有索引值。要求:时间复杂度小于O(n)

这个我当时想到的是循环遍历a,然后判断是否i in b,但是这个时间复杂度是O(n2),GG。最后面试官提醒了我一下hashmap,瞬间捶胸顿足……。最后自己想了一下,可以将b先转成字典,然后再使用in。
a = [5,3,1,5,4]
b = [5,3]
d = {}
for i in b:
d[i] = 0
res = []
l = len(a)
for i in range(l):
if a[i] in d:
res.append(i)
print(res)
1.2 如图,输入为这样,输出为那样,写吧……
输入几组数据,pid为-1的代表根节点。如果数据为非根节点,那么就要搜索此节点直至找到根节点。
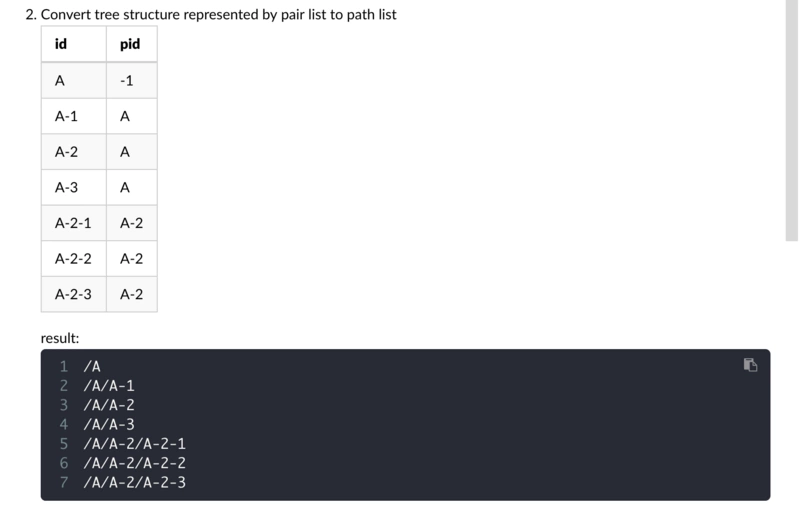
这个其实我知道考的是树的遍历,但是没见过这种形式的题,要自己构建输入数据的形式,一下子就懵了,再加上面试官在那一直盯着……唉,承认自己能力不足吧。后续自己写了一遍,大家可以看一下,有问题直接下面评论就可以。
d = {
"A":"-1",
"A-1":"A",
"A-2":"A",
"A-3":"A",
"A-2-1":"A-2",
"A-2-2":"A-2",
"A-2-3":"A-2"
}
res = []
def func(node):
array.append(node[0])
if node[1] == "-1":
return
func((node[1],d[node[1]]))
for i in d.items():
array = []
func(i)
string = "/".join(array[::-1])
res.append("/"+string)
for j in res:
print(j)
1.3 这个题太经典了。最短路径和。
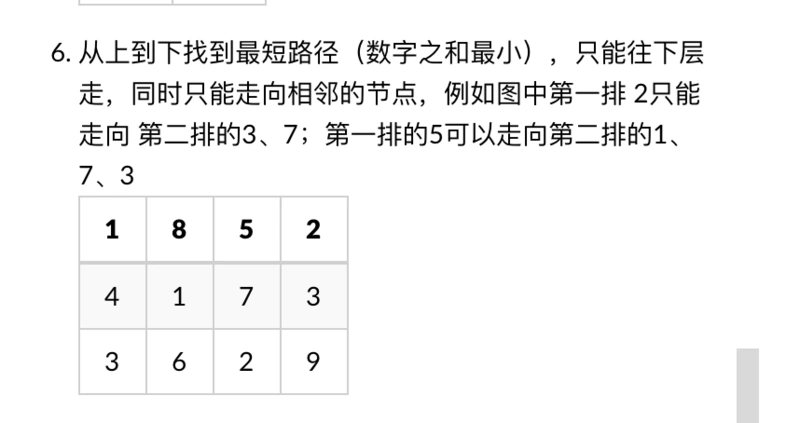
要注意是从第一行走到最后一行,而且只能向下或者斜向下走(我当时没看清就写,写成了从左上走到右下……)。我这里写的是动态规划的解法。Leetcode上有原题,解法不唯一。
array = [[1,8,5,2],
[4,1,7,3],
[3,6,2,9]]
x = len(array)
y = len(array[0])
dp = [[0 for i in range(y)] for j in range(x)]
# 遍历顺序是每行内的每列。所以遍历array中第一行只执行到if,dp中第一行就确定了,然后再确定dp第二行。
# 要注意两个边界条件
for i in range(x):
for j in range(y):
if i == 0:
dp[i][j] = array[i][j]
elif j == 0:
dp[i][j] = array[i][j] + min(dp[i-1][j], dp[i-1][j+1])
elif j == y-1:
dp[i][j] = array[i][j] + min(dp[i-1][j-1],dp[i-1][j])
else:
dp[i][j] = array[i][j] + min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])
# [[1, 8, 5, 2],
# [5, 2, 9, 5],
# [5, 8, 4, 14]]
print(min(dp[-1]))
# 4
2.其他面试问题
这里就不写答案了,大家可以百度或google一下。
2.1 什么是事务,事务的出现是为了解决什么问题
2.2 什么是聚簇索引
2.3 假如没有主键,InnoDB会以哪个字段建立主键
2.3 聊聊RabbitMQ中的connection与channel的关系,还有建立channel的一些规范或注意事项。
好文章,我在看❤️
评论
