图解 RepMLP
前言
本文提出了一个由多个全连接层构成的用于图像分类的模块RepMLP。全连接层能够高效地建模长距离依赖和位置模式,但不能很好地捕捉局部信息(擅长这件事情的是卷积)。我们在RepMLP中引入了卷积操作来捕捉局部信息,并在推理阶段将卷积核权重融入到全连接层中。该模块能充分利用全连接层的全局表征能力以及卷积层的局部捕捉特性,在图像分类任务上有不错的提升。
论文:RepMLPhttps://arxiv.org/abs/2105.01883
源代码:DingXiaoH/RepMLPhttps://github.com/DingXiaoH/RepMLP
介绍
在CNN中我们给卷积操作赋予了一个局部先验(也叫归纳偏置),卷积操作每次只处理相邻的元素。光有局部信息是不行的,需要给网络引入一定的全局信息。传统的CNN是通过卷积层的堆叠,来扩大感受野,以此获得全局信息。但这种做法效率低下,也带来很多优化的问题(以前训练很深的网络是很难的,后续通过正确的参数初始化和残差连接才逐步解决这一问题)。
此外CNN缺乏位置感知能力,因为一个卷积层在不同空间位置下是共享参数的。他没有考虑到各个空间位置特征的相对关系(Capsule Network也提到了)
最近的一些关于Vision Transformer的工作表明了在大量数据下,抛弃CNN的局部先验是可行的。本文尝试将全连接层替换部分卷积层中,以提供全局表征能力和位置感知能力。并将引入卷积层,赋予全连接层其不具备的捕捉局部信息能力。最后通过重参数化的方法,将卷积层和全连接层重参数化为一个全连接层,提升推理速度。
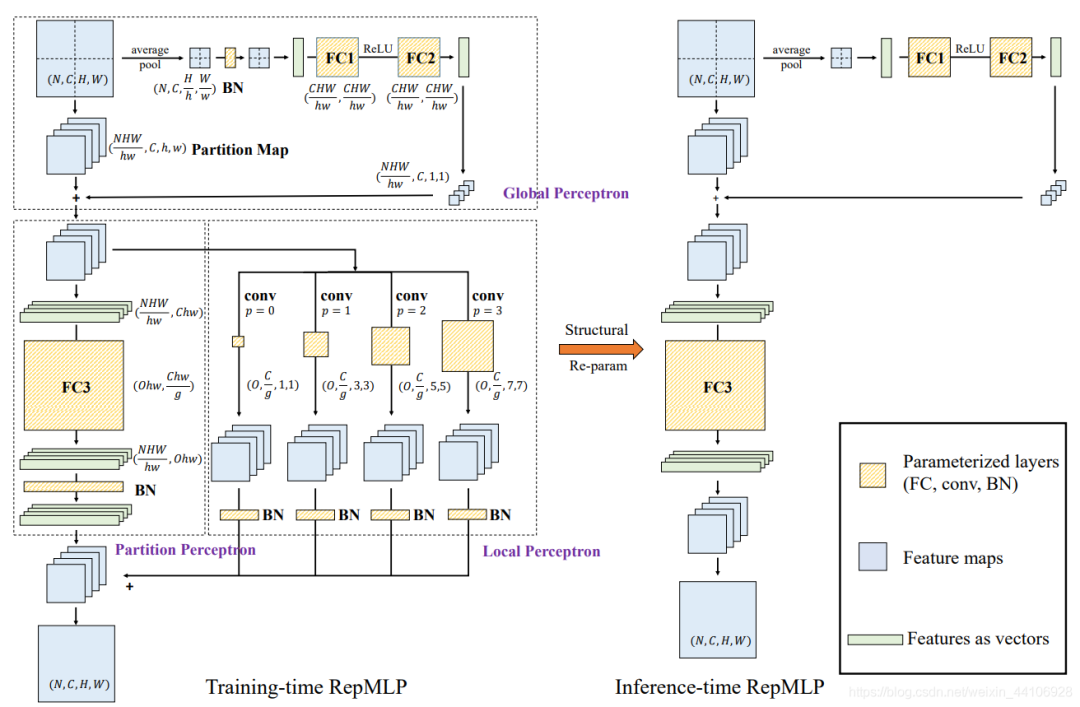
RepMLP主要分为Global Perceptron, Partition Perceptron 和 Local Perceptron 三部分,下面会分别讲解这两部分的做法
Global Perceptron
Global Perceptron模块首先对特征图进行切分
即张量从
其中h,w分别代表块的高,宽(这里切块的大小为7)
以让特征图能够在后续计算中共享参数,节省计算量。这样切分会破坏各部分之间的联系,为了给各切分后的特征图加入相关信息,Global Perceptron采取以下做法:
对每一个切分后的特征图进行平均池化 送入BN层+两个全连接层 将向量reshape成
与切分后的特征图进行广播相加
相关代码为:
def __init__(...):
if self.need_global_perceptron:
internal_neurons = int(self.C * self.h_parts * self.w_parts // fc1_fc2_reduction)
self.fc1_fc2 = nn.Sequential()
self.fc1_fc2.add_module('fc1', nn.Linear(self.C * self.h_parts * self.w_parts, internal_neurons))
self.fc1_fc2.add_module('relu', nn.ReLU())
self.fc1_fc2.add_module('fc2', nn.Linear(internal_neurons, self.C * self.h_parts * self.w_parts))
if deploy:
self.avg = nn.AvgPool2d(kernel_size=(self.h, self.w))
else:
self.avg = nn.Sequential()
self.avg.add_module('avg', nn.AvgPool2d(kernel_size=(self.h, self.w)))
self.avg.add_module('bn', nn.BatchNorm2d(num_features=self.C))
def forward(...):
if self.need_global_perceptron:
v = self.avg(inputs)
v = v.reshape(-1, self.C * self.h_parts * self.w_parts)
v = self.fc1_fc2(v)
v = v.reshape(-1, self.C, self.h_parts, 1, self.w_parts, 1)
inputs = inputs.reshape(-1, self.C, self.h_parts, self.h, self.w_parts, self.w)
inputs = inputs + v
Partition Perceptron
Partition Perceptron模块含有一个BN层和一个全连接层。其中为了节省参数量,采用分组全连接层(Pytorch没有相关OP,这里采用1x1的分组卷积来等价代替)。Partition Perceptron做法如下:
将张量从
接入1x1的组卷积和BN层 将向量reshape回原输入的形状
相关代码如下:
def __init__():
self.fc3 = nn.Conv2d(self.C * self.h * self.w, self.O * self.h * self.w, 1, 1, 0, bias=deploy, groups=fc3_groups)
self.fc3_bn = nn.Identity() if deploy else nn.BatchNorm1d(self.O * self.h * self.w)
def forward():
# Feed partition map into Partition Perceptron
fc3_inputs = partitions.reshape(-1, self.C * self.h * self.w, 1, 1)
fc3_out = self.fc3(fc3_inputs)
fc3_out = fc3_out.reshape(-1, self.O * self.h * self.w)
fc3_out = self.fc3_bn(fc3_out)
fc3_out = fc3_out.reshape(-1, self.h_parts, self.w_parts, self.O, self.h, self.w)
Local Perceptron
Local Perceptron模块将切分后的特征图喂入卷积层,其中卷积层的卷积核大小分别为1, 3, 5, 7(卷积核大小需要小于特征图,而之前切分时我们设置的大小为7)。
需要注意的是为了后续的特征相加操作,这里卷积层都需要做padding。另外为了减少参数量,这里也是采用的分组卷积。这里的分组数需要与Partition Perceptron的分组数一致
具体做法如下:
将特征图同时送入到卷积核大小为1, 3, 5, 7的卷积层 送入BN层 与 Partition Perceptron的输出相加
相关代码如下:
def __init__(...):
self.reparam_conv_k = reparam_conv_k
if not deploy and reparam_conv_k is not None:
for k in reparam_conv_k:
conv_branch = nn.Sequential()
conv_branch.add_module('conv', nn.Conv2d(in_channels=self.C, out_channels=self.O, kernel_size=k, padding=k // 2, bias=False, groups=fc3_groups))
conv_branch.add_module('bn', nn.BatchNorm2d(self.O))
self.__setattr__('repconv{}'.format(k), conv_branch)
def forward(...):
# Feed partition map into Local Perceptron
if self.reparam_conv_k is not None and not self.deploy:
conv_inputs = partitions.reshape(-1, self.C, self.h, self.w)
conv_out = 0
for k in self.reparam_conv_k:
conv_branch = self.__getattr__('repconv{}'.format(k))
conv_out += conv_branch(conv_inputs)
conv_out = conv_out.reshape(-1, self.h_parts, self.w_parts, self.O, self.h, self.w)
fc3_out += conv_out # fc3_out是前面Partition Perceptron的输出
重参数化——将卷积权重融合到全连接层
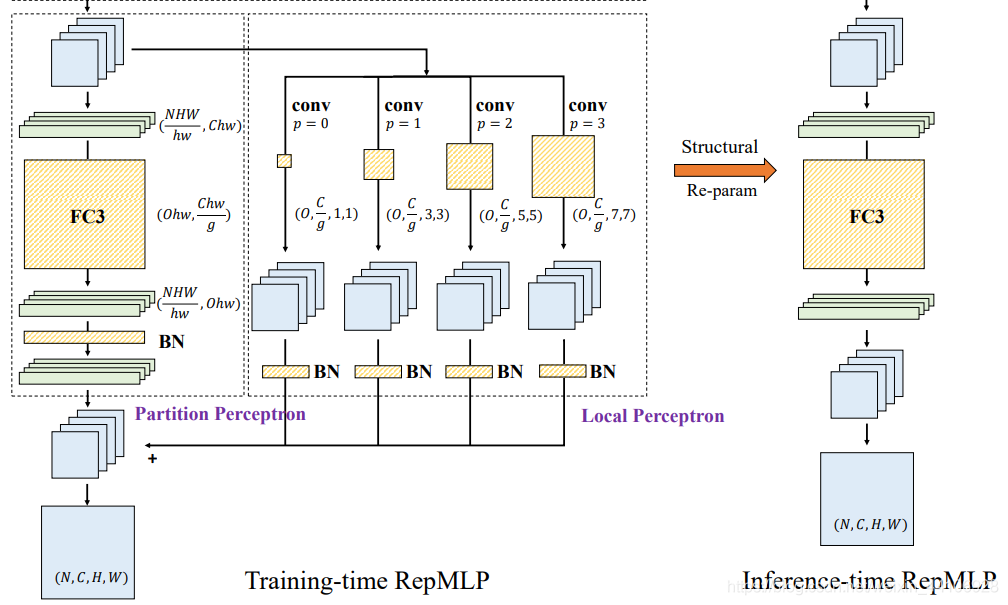
在推理阶段,我们会把 Local Perceptron 和 Partition Perceptron 这两部分融合成一个全连接层
这是我觉得本文最大的亮点,也是最难理解的部分,下面我会拿一些图例来讲解这一重参数化过程。
矩阵乘法具有可加性, Partition Perceptron 的全连接层和 Local Perceptron 的卷积层相加可以写为:
而我们也知道卷积是一种稀疏化的矩阵乘法,所以存在一个等价的权重转换
熟悉矩阵乘的话,我们可以知道在其中插入一个单位矩阵,是不会改变矩阵的结果
所以有
而
可以看成是卷积核F在单位矩阵上进行卷积得到的结果,具体做法如下:
将单位矩阵reshape为
单位矩阵和卷积核F做卷积操作 将结果reshape成
可能看到这里还是有点迷糊,下面我会画几张图
这里以4x4的特征图,3x3的卷积核来示范
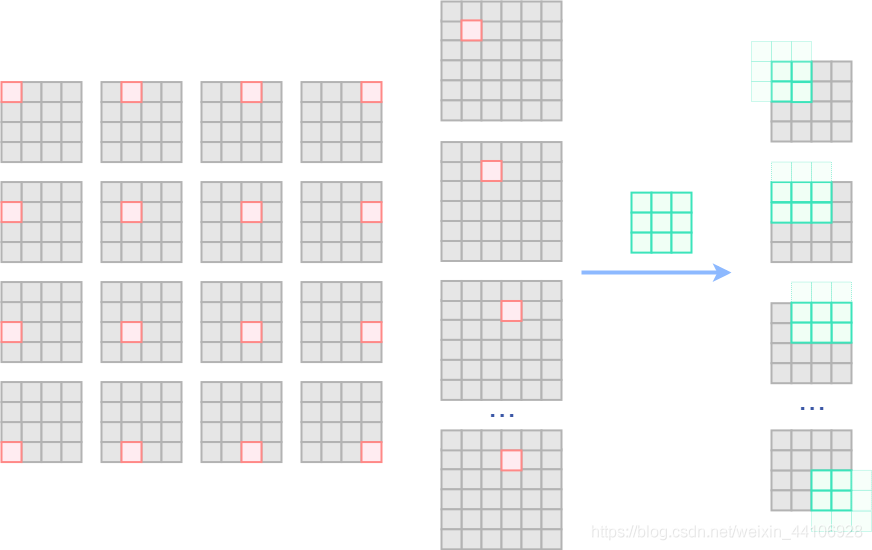
首先我们构造出对应的单位矩阵,为了让3x3卷积得到的特征图大小不变,这里做了padding。
要注意的是这里的单位矩阵是在Batch维度上排列(而不是在通道维上排列),所以卷积核出来以后同样也有16个独立的特征图出来。
这里我以浅绿色来代表没有参与运算的卷积核权重,深绿色则是参与实际运算的卷积核权重
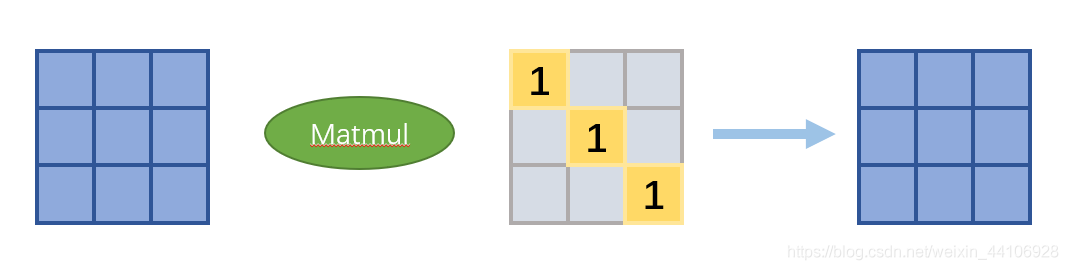
然后我们取第一个矩阵进行观察,他摊平以后与输入做矩阵乘入下图所示
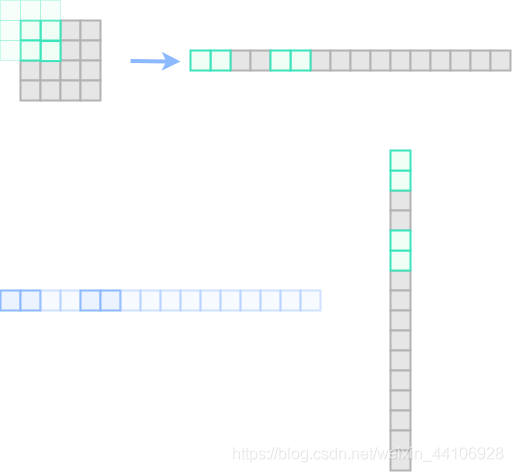
其中深色部分代表参与实际运算的元素
然后我们回到原始的卷积操作,看第一步卷积操作分别是与哪些元素进行相乘求和

可以发现和我们上面的矩阵乘是完全等价的,后续的卷积操作也如上推导
一个简单的示例如下:
import torch
x = torch.randn(1, 1, 4, 4)
conv_kernel = torch.randn(size=(1, 1, 3, 3)) # 初始化一个卷积核权重
conv_out = torch.nn.functional.conv2d(x, conv_kernel, padding=1)
identity = torch.eye(16).repeat(1, 1).reshape(16, 1, 4, 4) # 得到一个单位矩阵
fc_k = torch.nn.functional.conv2d(identity, conv_kernel, padding=1)
fc_k = torch.reshape(fc_k, (16, 16))
print("Conv: ", conv_out) # 输出卷积结果
x_flatten = torch.reshape(x, (1, 16)) # 展平输入向量
matmul = torch.matmul(x_flatten, fc_k)
print("matmul: ", matmul) # 输出矩阵乘结果
这里仅仅是推导了常规卷积转换的思路,实际使用的还是分组卷积,这里就不再做推导
下面是作者对应实现的代码:
def _convert_conv_to_fc(self, conv_kernel, conv_bias):
I = torch.eye(self.C * self.h * self.w // self.fc3_groups).repeat(1, self.fc3_groups).reshape(self.C * self.h * self.w // self.fc3_groups, self.C, self.h, self.w).to(conv_kernel.device)
fc_k = F.conv2d(I, conv_kernel, padding=conv_kernel.size(2)//2, groups=self.fc3_groups)
fc_k = fc_k.reshape(self.O * self.h * self.w // self.fc3_groups, self.C * self.h * self.w).t()
fc_bias = conv_bias.repeat_interleave(self.h * self.w)
return fc_k, fc_bias
此外,还做了全连接层和BN层的融合,在之前的图解RepVGG有讲解过,这里就不展开了。
实验结果
实验就直接看图了,xiaohan的东西牛逼好用就完事了
下面是基于 Bottleneck Block 增加 RepMLP 模块
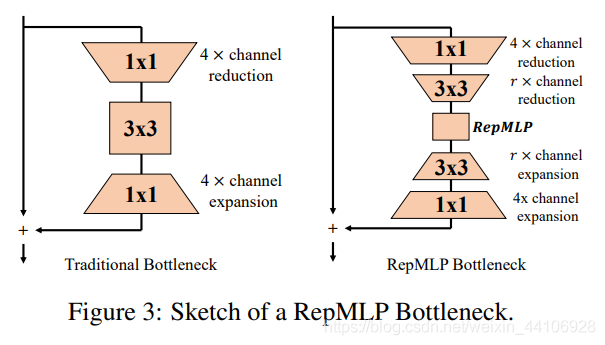
在 stage4 中不同分组卷积的结果:
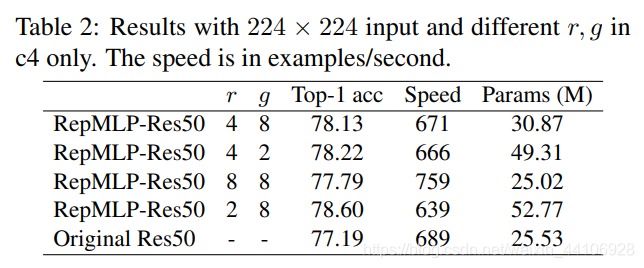
ImageNet的对比:
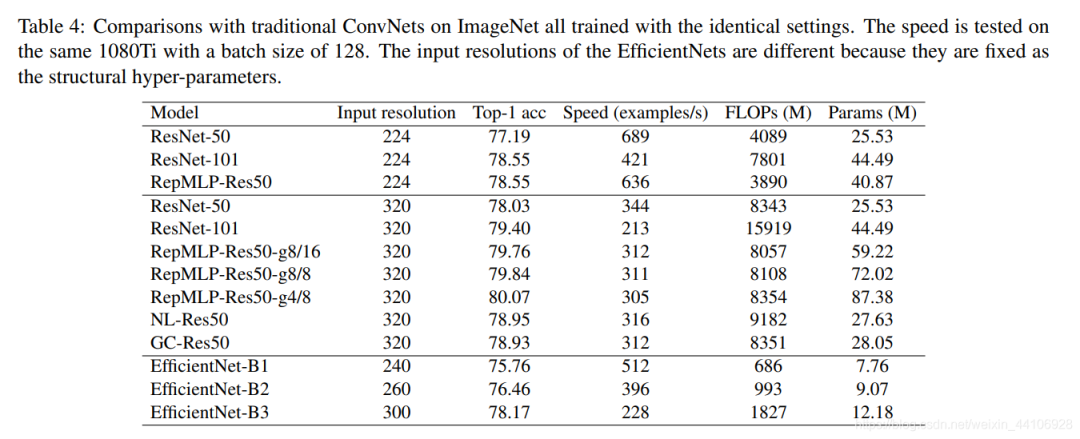
小结
这篇工作又给重参数方向填了一块重要的拼图,充分利用了卷积层和全连接层各自的特性,并将卷积核巧妙的融入到全连接层中。能给模型涨点,推理速度也没有降低很多(EfficientNet出来挨打),xiaohan yyds!(期待后续能对注意力进行重参数化:D)
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:
