运筹学教学|快醒醒,你的熟人拉格朗日又来了!!-技术圈

拉

格朗日松弛算法，啥，怎么运筹学也有拉格朗日了啊？为什么哪里都有他？那么拉格朗日松弛算法到底讲了什么呢？本期，小编将带你走进拉格朗日松弛的世界。

约瑟夫·路易斯·拉格朗日

★ 目录 ★

拉格朗日松弛方法简介

拉格朗日松弛方法基础

求解拉格朗日界的次梯度方法

一个算例求解

拉格朗日松弛方法简介

当遇到一些很难求解的模型，但又不需要去求解它的精确解，只需要给出一个次优解或者解的上下界，这时便可以考虑采用松弛模型的方法加以求解。

对于一个整数规划问题，拉格朗日松弛放松模型中的部分约束。这些被松弛的约束并不是被完全去掉，而是利用拉格朗日乘子在目标函数上增加相应的惩罚项，对不满足这些约束条件的解进行惩罚。

拉格朗日松弛之所以受关注，是因为在大规模的组合优化问题中，若能在原问题中减少一些造成问题“难”的约束，则可使问题求解难度大大降低，有时甚至可以得到比线性松弛更好的上下界。

拉格朗日松弛方法基础

求解拉格朗日界的次梯度方法

为了方便各位读者理解，我们直接放上流程图如下

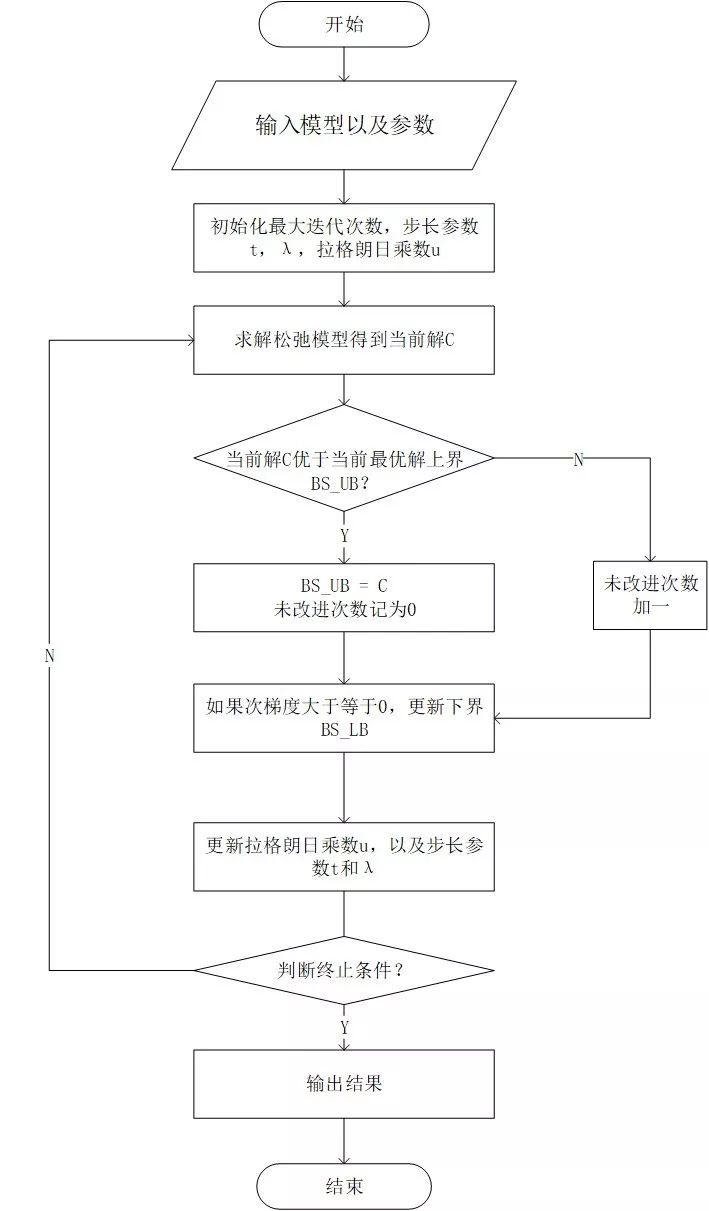
其中各个参数的计算方式参照第二节中给出的公式来计算。

一个算例求解

MainFrame.java

package lagranger;
import java.io.IOException;import ilog.concert.IloException;
public class MainFrame {  double best_ub;  double best_lb;  double best_mu;  double[] best_sl;  Subproblem sp;  public MainFrame()   {    best_lb = 0;    best_ub = 1e10;    sp = new Subproblem();    best_sl = new double[4];  }  // 次梯度方法求解拉格朗日对偶  public void solve(double min_step_size, int max_iter) throws IOException, IloException  {    int iter = 0;    int non_improve = 0;    int max_non_improve = 3;      double lambda = 2;          double step_size = 1;        double mu = 0;         // 初始化拉格朗日乘子    sp.construct(mu);      // 松弛第一个约束条件的拉格朗日松弛    while(iter++ < max_iter)    {      sp.changeObj(mu);      if (sp.solve() == false)       {        System.out.println("The Lagrangian problem solve wrong!");        System.exit(0);      }      // 更新上界      if(sp.opt_cost < best_ub)      {        best_ub = sp.opt_cost;        best_mu = mu;        for(int i = 0; i < best_sl.length; i++)          best_sl[i] = sp.opt_x[i];        non_improve = 0;      }      else        non_improve++;      System.out.println("iter " + iter + "******************************");      System.out.println("best lb " + best_lb);      System.out.println("best ub " + best_ub);      System.out.println("current ub " + sp.opt_cost);      System.out.println("mu " + mu);      double subgradient = 8*sp.opt_x[0] + 2*sp.opt_x[1] + sp.opt_x[2] + 4*sp.opt_x[3] - 10;      mu = Math.max(0, mu + step_size * subgradient);      // 满足原问题约束的可行解可以作为原问题的下界      if (subgradient <= 0)       {        double current_lb = 16*sp.opt_x[0] + 10*sp.opt_x[1] + 4*sp.opt_x[3];        if (current_lb > best_lb)           best_lb = current_lb;      }      // 上界未更新达到一定次数      if(non_improve >= max_non_improve)      {        lambda /= 2;        non_improve = 0;      }      double dist = Math.pow(subgradient, 2);
      // 迭代停止条件2和3      if(dist <= 0.0 || best_lb >= best_ub - 0.0000001)        break;      step_size = lambda * (sp.opt_cost - best_lb) / dist;
      // 迭代停止条件4      if(step_size < min_step_size)        break;    }  }  public static void main(String[] args) throws IOException, IloException   {    MainFrame mf = new MainFrame();    mf.solve(0.01, 10);    System.out.println("result: ");    System.out.println("best_lb: " + mf.best_lb);    System.out.println("best_ub: " + mf.best_ub);    double gap = Math.round((mf.best_ub - mf.best_lb) *  10000 / mf.best_ub) / 100;    System.out.println("gap: " + gap + "%");  }}

Subproblem.java

package lagranger;
import ilog.concert.*;import ilog.cplex.IloCplex;
public class Subproblem {  IloCplex cplex;  double opt_cost;  double mu;  double[] opt_x;  IloNumVar[] X;  public void construct(double cmu) throws IloException {    cplex = new IloCplex();    cplex.setOut(null);    mu = cmu;    // 4个变量    X  = new IloNumVar[4];    for(int i = 0; i < X.length; i++)      X[i] = cplex.numVar(0.0, 1, IloNumVarType.Int, "X" + i);    // 初始目标函数    IloLinearNumExpr obj = cplex.linearNumExpr();    obj.addTerm(16-8*mu, X[0]);    obj.addTerm(10-2*mu, X[1]);    obj.addTerm(0-mu, X[2]);    obj.addTerm(4-4*mu, X[3]);    cplex.addMaximize(obj);    // 约束条件    IloLinearNumExpr expr1 = cplex.linearNumExpr();    expr1.addTerm(1, X[0]);    expr1.addTerm(1, X[1]);    cplex.addLe(expr1, 1);    IloLinearNumExpr expr2 = cplex.linearNumExpr();    expr1.addTerm(1, X[2]);    expr1.addTerm(1, X[3]);    cplex.addLe(expr2, 1);  }  public void changeObj(double cmu) throws IloException {    // 目标函数    mu = cmu;    IloLinearNumExpr new_obj = cplex.linearNumExpr();    new_obj.addTerm(16-8*mu, X[0]);    new_obj.addTerm(10-2*mu, X[1]);    new_obj.addTerm(0-mu, X[2]);    new_obj.addTerm(4-4*mu, X[3]);    cplex.getObjective().clearExpr();    cplex.getObjective().setExpr(new_obj);  }  public boolean solve() throws IloException {    if(this.cplex.solve())    {      opt_cost = cplex.getObjValue() + 10*mu;      opt_x = new double[X.length];      for (int i = 0; i < X.length; i++)         opt_x[i] = cplex.getValue(X[i]);      return true;    }    cplex.exportModel("model.lp");    return false;  }}

运行之后我们可以得到如下结果

有兴趣的小伙伴一定要下载代码自己运行一遍哦~代码和参考资料将会在留言区给出~注意，在这个代码中，我们使用了之前讲到的Cplex工具，如果有不会使用的小伙伴请点击下方传送门

干货|十分钟快速掌握CPLEX求解VRPTW数学模型（附JAVA代码及CPLEX安装流程）

参考文献

【1】Marshall L. Fisher, The Lagrangian Relaxation Method for Solving Integer Programming Problems. Management Science, Vol. 27, No. 1 (Jan., 1981), pp. 1-18

【如对代码有疑问，可联系小编，可以提供有偿辅导服务】

【有偿辅导纯属个人行为，与团队无关】

-The End-

文案 / 排版 / 代码苏锷（研一）

指导老师 / 秦虎华中科技大学管理学院 tigerqin@hust.edu.cn

审稿老师/刘林冬中国科学技术大学管理学院 ldliu(at)ustc.edu.cn

如对代码有疑问，可联系小编，无偿提供服务。

苏锷（华中科技大学管理学院、es1996@foxmail.com)