每日一道 LeetCode (56)：四数之和

每天 3 分钟，走上算法的逆袭之路。

前文合集

每日一道 LeetCode 前文合集

代码仓库

GitHub：https://github.com/meteor1993/LeetCode

Gitee：https://gitee.com/inwsy/LeetCode

题目：四数之和

难度：中等

题目来源：https://leetcode-cn.com/problems/4sum/

给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。

注意：

答案中不可以包含重复的四元组。

示例：

给定数组 nums = [1, 0, -1, 0, -2, 2]，和 target = 0。

满足要求的四元组集合为：
[
  [-1,  0, 0, 1],
  [-2, -1, 1, 2],
  [-2,  0, 0, 2]
]

解题思路

这道题有点方，虽然前面曾经做过一个三数之和的题，但是看到这个题完全没和前面的那道题产生联系。

最蠢的方案就是套 4 层循环，暴力循环 4 次，虽然我没这么干，但是这么干肯定超时，我在题解的评论里面见到有人真的用了 4 层循环，真的猛士，这道题 4 层循环想要写通并不是那么简单的。

除了 4 层循环，那么 3 层循环行不行，当然可以，答案上给出来的就是三重循环。

套路还是和之前的三数之和一样，使用双指针，使用两层循环分别枚举前两个数，之后使用双指针在同一重循环中枚举剩下两个数。

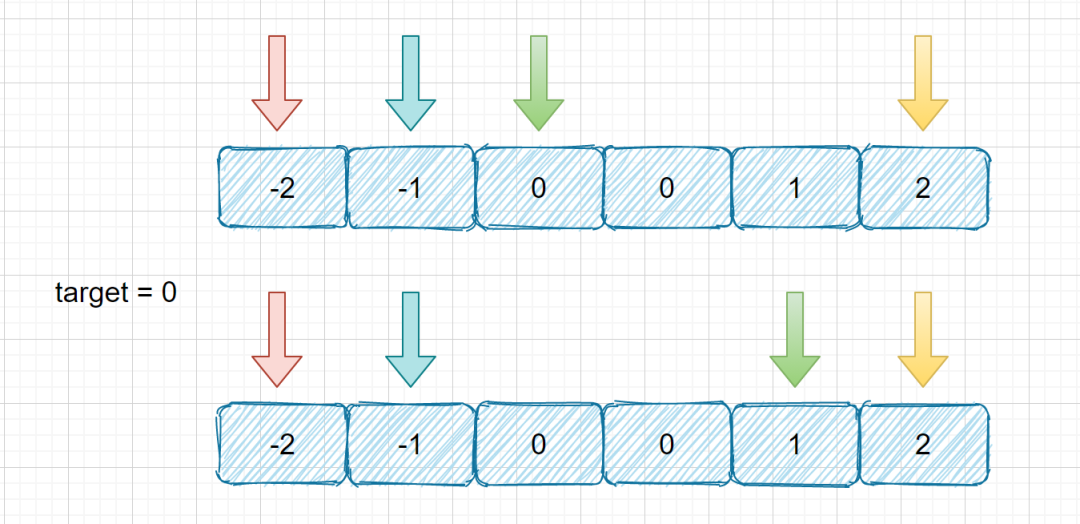
首先确定红色和蓝色的 i 和 j ，然后在剩下的数中寻找目标，向右移动绿色的箭头，直到找到一个结果，把这个结果存下来，继续移动，当绿色移动结束后，将蓝色向右移动一位，接着移动绿色的箭头进行寻找，直到红色的箭头移动至 num.length - 3 的位置为止。

代码上我加了注释，看起来应该比较清晰：

public class Solution {
    public List> fourSum(int[] nums, int target) {
        List> result = new ArrayList<>();
        if (nums == null || nums.length < 4) return result;
        // 先对数组做排序
        Arrays.sort(nums);
        int length = nums.length;
        for (int i = 0; i < length - 3; i++) {
            // 特殊情况判断
            // 最小数字不可重复
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            // 如果和大于 target ，那么接下来所有的结果肯定都大于 target ，直接 break
            if (nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) break;
            // 最大的结果也小于 target 时，直接最小数进入下一次循环
            if (nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) continue;
            for (int j = i + 1; j < length - 2; j++) {
                // 特殊情况判断，和最小的数字判断规则相同
                if (j > i + 1 && nums[j] == nums[j - 1]) continue;
                if (nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) break;
                if (nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) continue;
                // left 和 right 分别代表第 3 、4 个数
                int left = j + 1, right = length - 1;
                while (left < right) {
                    int sum = nums[i] + nums[j] + nums[left] + nums[right];
                    // 当结果和 target 相同时
                    if (sum == target) {
                        // 结果存入 result 中
                        result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                        // 去重第三个数
                        while (left < right && nums[left] == nums[left + 1]) left++;
                        left++;
                        // 去重第四个数
                        while (left < right && nums[right] == nums[right - 1]) right--;
                        right--;
                    } else if (sum < target) {
                        left++;
                    } else {
                        right--;
                    }
                }
            }
        }
        return result;
    }
}