用统计学玩《鱿鱼游戏》

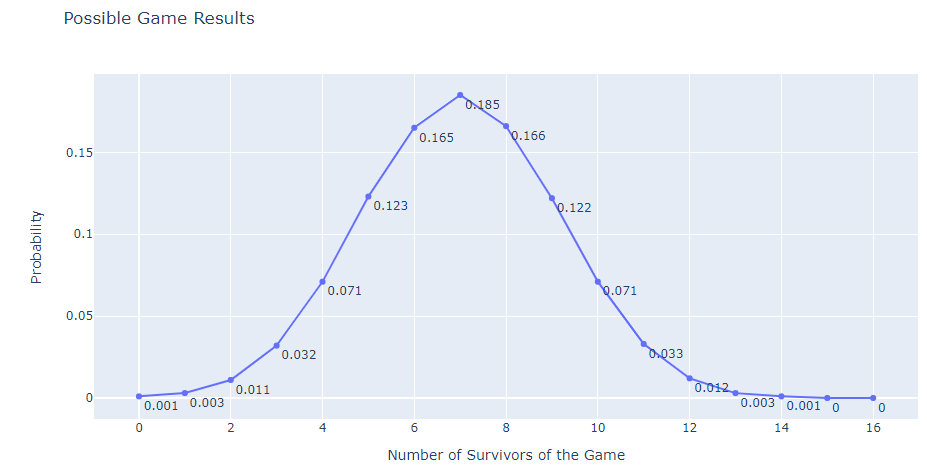
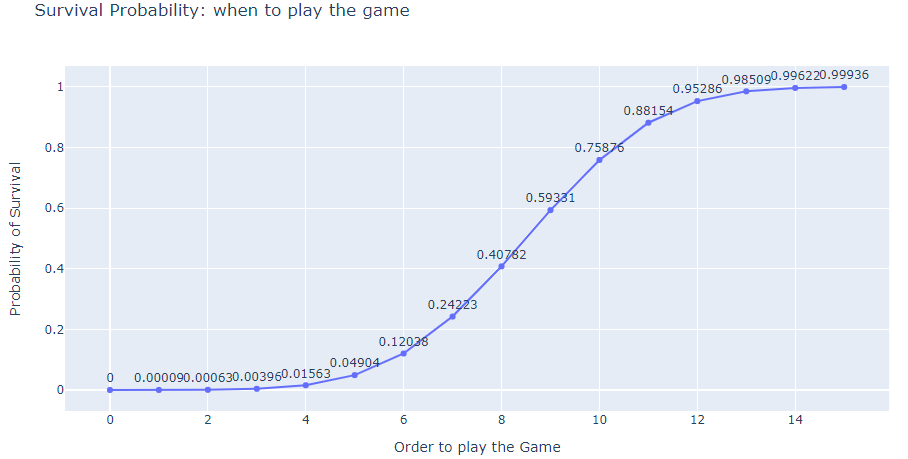
• 只有3名幸存者活下来了。如果再次玩游戏，是否有可能有更多（或更少的幸存者）？出现其他结果的概率是多少？
• 这个游戏的生存概率是3/16吗？生存概率与游戏顺序有什么关系？
• 如何根据猜对了多少玻璃来判断玩家是否是骗子？
• 如何在这场比赛中生存？

• 如果玩家没有死，他们会继续行走。
• 玩家随机选择玻璃(即猜对每一行的概率是0.5)-不允许作弊。
• 在模拟游戏中并不考虑时间效应(通过取消模拟中的时间限制对玩家表示一些怜悯，其实是简化了我们的计算)。

Everyone Is Equal While They Play This Game. Here, The Players Get To Play A Fair Game Under The Same Conditions. Those People Suffered From Inequality And Discrimination Out In The World, And We’re Giving Them The Last Chance To Fight Fair And Win.

— The Front Man[2]

• 先验比率：作弊与非作弊是 1/99
• 问题：不作弊的概率为1/(2⁵)=1/32，作弊猜对5次的概率为1，所以似然比为1/(1/32)=32
• 后验比率 = 先验比率 * 似然比率 = 1/99 * 32 = 32/99
• 后验：作弊概率 = 32/(32+99) = ~24%。

• 先验比率：作弊与非作弊是 1/99
• 问题：不作弊的概率为1/(2¹⁰)=1/1024，作弊者猜对10次的概率为1，所以似然比为1/(1/1024)=1024
• 后验比率 = 先验比率 * 似然比率 = 1/99 * 1024 = 1024/99
• 后验：作弊概率 = 1024/(1024+99) = ~91.2%。