LeetCode刷题实战115：不同的子序列-技术圈

算法的重要性，我就不多说了吧，想去大厂，就必须要经过基础知识和业务逻辑面试+算法面试。所以，为了提高大家的算法能力，这个公众号后续每天带大家做一道算法题，题目就从LeetCode上面选！

今天和大家聊的问题叫做 不同的子序列，我们先来看题面：

https://leetcode-cn.com/problems/distinct-subsequences/

Given two strings s and t, return the number of distinct subsequences of s which equals t.

A string's subsequence is a new string formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., "ACE" is a subsequence of "ABCDE" while "AEC" is not).

It's guaranteed the answer fits on a 32-bit signed integer.

题意

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个子序列是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

题目数据保证答案符合 32 位带符号整数范围。

样例

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
(上箭头符号 ^ 表示选取的字母)
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

解题

https://www.cnblogs.com/powercai/p/11116692.html

动态规划

dp[i][j]代表T前i字符串可以由S前j字符串组成最多个数.

所以动态方程:

当 S[j] == T[i], dp[i][j] = dp[i-1][j-1] + dp[i][j-1];

当S[j] != T[i], dp[i][j] = dp[i][j-1]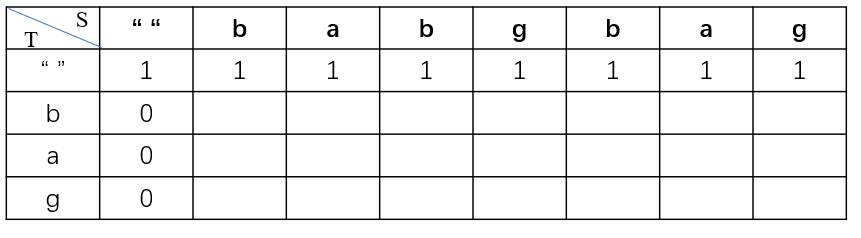

举个例子,如示例的

对于第一行, T为空,因为空集是所有字符串子集, 所以我们第一行都是1

对于第一列, S为空,这样组成T个数当然为0了

至于下面如何进行,大家可以通过动态方程,自行模拟一下!

class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[t.length() + 1][s.length() + 1];
        for (int j = 0; j < s.length() + 1; j++) dp[0][j] = 1;
        for (int i = 1; i < t.length() + 1; i++) {
            for (int j = 1; j < s.length() + 1; j++) {
                if (t.charAt(i - 1) == s.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];
                else dp[i][j] = dp[i][j - 1];
            }
        }
        return dp[t.length()][s.length()];
    }
}