获取神经网络的计算量和参数量
作者:DengBoCong 文仅交流,侵删
Github:本文代码放在该项目中:https://github.com/DengBoCong/nlp-paper
说明:讲解时会对相关文章资料进行思想、结构、优缺点,内容进行提炼和记录,相关引用会标明出处,引用之处如有侵权,烦请告知删除。
目录:
全连接层的计算量和参数量估计
激活函数的计算量估计
LSTM的计算量和参数量估计
卷积层的计算量和参数量估计
深度可分离卷积的计算量和参数量估计
Batch Normalization的计算量和参数量估计
其他层的计算量和参数量估计
对于深度学习模型来说,拥有一个非常好的设计思路和体系架构非常重要,对模型性能的影响非常之大,所以对于模型的研究倾向于在模型性能上的表现。但是对于商业应用来说,算法模型落地的另一个重要考量就是在满足业务场景内存占用、计算量等需要的同时,保证算法的性能,这个研究对于移动端的模型部署更加明显,这有利于压缩应用的体积。最近这段时间正好在研究关于移动端模型部署(TensorFlow Lite用的不是很顺心呀),所以要仔细研究一下模型的参数量等,这不仅可以让我们对模型的大小进行了解,还能更好的调整结构使得模型响应的更快。
可能有时候觉得,模型的大小需要计算嘛,直接保存大小直接看不就完事儿了?运行速度就更直接了,多运行几次取平均速度不就行了嘛?so easy?这个想法也没啥错,但是大前提是你得有个整型的模型呀(训练成本多高心里没数嘛),因此很多时候我们想要在模型设计之初就估计一下模型的大小以及可能的运行速度(通过一些指标侧面反应速度),这个时候我们就需要更深入的理解模型的内部结构和原理,从而通过估算模型内部的参数量和计算量来对模型的大小和速度进行一个初步评估。
一个朴素的评估模型速度的想法是评估它的计算量。一般我们用FLOPS,即每秒浮点操作次数FLoating point OPerations per Second这个指标来衡量GPU的运算能力。这里我们用MACC,即乘加数Multiply-ACCumulate operation,或者叫MADD,来衡量模型的计算量。不过这里要说明一下,用MACC来估算模型的计算量只能大致地估算一下模型的速度。模型最终的的速度,不仅仅是和计算量多少有关系,还和诸如内存带宽、优化程度、CPU流水线、Cache之类的因素也有很大关系。
下面我们对计算量来进行介绍和定义,方便我们后续展开层的讲解:
神经网络中的许多计算都是点积,例如:
y = w[0]*x[0] + w[1]*x[1] + w[2]*x[2] + ... + w[n-1]*x[n-1]
此处,  和
和  是两个向量,结果
是两个向量,结果  是标量(单个数字)。对于卷积层或完全连接的层(现代神经网络中两种主要类型的层),
是标量(单个数字)。对于卷积层或完全连接的层(现代神经网络中两种主要类型的层),  是该层的学习权重,
是该层的学习权重,  是该层的输入。我们将
是该层的输入。我们将  计数为一个乘法累加或1个MACC,这里的“累加”运算是加法运算,因为我们将所有乘法的结果相加,所以上式具有
计数为一个乘法累加或1个MACC,这里的“累加”运算是加法运算,因为我们将所有乘法的结果相加,所以上式具有  个这样的MACC(从技术上讲,上式中只有
个这样的MACC(从技术上讲,上式中只有  个加法,比乘法数少一个,所以这里知识认为MACC的数量是一个近似值)。就FLOPS而言,因为有
个加法,比乘法数少一个,所以这里知识认为MACC的数量是一个近似值)。就FLOPS而言,因为有  个乘法和
个乘法和  个加法,所以点积执行
个加法,所以点积执行  FLOPS,因此,MACC大约是两个FLOPS。现在,我们来看几种不同的层类型,以了解如何计算这些层的MACC数量。
FLOPS,因此,MACC大约是两个FLOPS。现在,我们来看几种不同的层类型,以了解如何计算这些层的MACC数量。
注意了:下面的阐述如果没有特别说明,默认都是batch为1。
01
在完全连接的层中,所有输入都连接到所有输出。对于具有  输入值和
输入值和  输出值的图层,其权重
输出值的图层,其权重  可以存储在
可以存储在  矩阵中。全连接层执行的计算为:
矩阵中。全连接层执行的计算为:

在这里,  是
是  输入值的向量,
输入值的向量,  是包含图层权重的
是包含图层权重的  矩阵,
矩阵,  是
是  偏差值的向量,这些值也被相加。结果
偏差值的向量,这些值也被相加。结果  包含由图层计算的输出值,并且也是大小
包含由图层计算的输出值,并且也是大小  的向量。对于完全连接层来说,矩阵乘法为
的向量。对于完全连接层来说,矩阵乘法为  ,其中具有
,其中具有  个MACC(和权重矩阵
个MACC(和权重矩阵  大小一样),对于偏置
大小一样),对于偏置  ,正好补齐了前面我们所说的点积中正好少一个加法操作。因此,比如一个具有300个输入神经元和100个输出神经元的全连接层执行
,正好补齐了前面我们所说的点积中正好少一个加法操作。因此,比如一个具有300个输入神经元和100个输出神经元的全连接层执行  个MACC。特别提示:上面我们讨论的批次大小
个MACC。特别提示:上面我们讨论的批次大小  需要具体计算需要乘上Batch。
需要具体计算需要乘上Batch。
也就是说,通常,将长度为  的向量与
的向量与  矩阵相乘以获得长度为
矩阵相乘以获得长度为  的向量,则需要
的向量,则需要  MACC或
MACC或  FLOPS。
FLOPS。
上面我们讨论了全连接层的计算量,那么它的参数量是多少呢?这个应该很容易就算出来,对于全连接层而言,它的参数分别是权重  和 偏置
和 偏置  ,所以对于上面的例子中具有300个输入神经元和100个输出神经元的全连接层的参数量是:
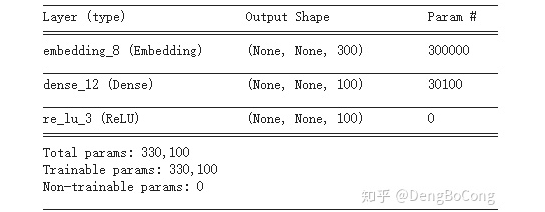
,所以对于上面的例子中具有300个输入神经元和100个输出神经元的全连接层的参数量是:  ,这个很容易进行验证,下图是使用TensorFlow进行验证参数量:
,这个很容易进行验证,下图是使用TensorFlow进行验证参数量:

02
通常,一个层后面紧接着就是非线性激活函数,例如ReLU或sigmoid,理所当然的计算这些激活函数需要时间,但在这里我们不用MACC进行度量,而是使用FLOPS进行度量,原因是它们不做点积,一些激活函数比其他激活函数更难计算,例如一个ReLU只是:

这是在GPU上的一项操作,激活函数仅应用于层的输出,例如在具有  个输出神经元的完全连接层上,ReLU计算
个输出神经元的完全连接层上,ReLU计算  次,因此我们将其判定为
次,因此我们将其判定为  FLOPS。而对于Sigmoid激活函数来说,有不一样了,它涉及到了一个指数,所以成本更高:
FLOPS。而对于Sigmoid激活函数来说,有不一样了,它涉及到了一个指数,所以成本更高:

在计算FLOPS时,我们通常将加,减,乘,除,求幂,平方根等作为单个FLOP进行计数,由于在Sigmoid激活函数中有四个不同的运算,因此将其判定为每个函数输出4 FLOPS或总层输出  FLOPS。所以实际上,通常不计这些操作,因为它们只占总时间的一小部分,更多时候我们主要对(大)矩阵乘法和点积感兴趣,所以其实我们通常都是忽略激活函数的计算量。
FLOPS。所以实际上,通常不计这些操作,因为它们只占总时间的一小部分,更多时候我们主要对(大)矩阵乘法和点积感兴趣,所以其实我们通常都是忽略激活函数的计算量。
对于参数量?注意了它压根没有参数,请看它们的公式,用TensorFlow验证如下:
03
关于LSTM的原理可以参考这一篇文章
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
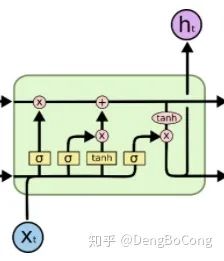
 。其中,第一层是
。其中,第一层是  和
和  的结合,维度就是embedding_size + hidden_size,第二层就是输出层,维度为 hidden_size,则它的计算量按照上文我们对全连接层的阐述,易得MACC为:
的结合,维度就是embedding_size + hidden_size,第二层就是输出层,维度为 hidden_size,则它的计算量按照上文我们对全连接层的阐述,易得MACC为:(embedding_size + hidden_size) * hidden_size * 4 ,其中共有八个加,减,乘,除,求幂,平方根等计算,所以计算量为:(embedding_size + hidden_size) * hidden_size * 8个FLOPS。除此之外,LSTM除了在四个非线性变换中的计算,还有三个矩阵乘法(不是点积)、一个加法、一个tanh计算,其中三个矩阵乘法都是shape为(batch, hidden_size),则这四个运算的计算量为:batch * hidden_size + batch * hidden_size + batch * hidden_size + batch * hidden_size + batch * hidden_size * 8,综上所述,LSTM的计算量为:
,其中共有八个加,减,乘,除,求幂,平方根等计算,所以计算量为:(embedding_size + hidden_size) * hidden_size * 8个FLOPS。除此之外,LSTM除了在四个非线性变换中的计算,还有三个矩阵乘法(不是点积)、一个加法、一个tanh计算,其中三个矩阵乘法都是shape为(batch, hidden_size),则这四个运算的计算量为:batch * hidden_size + batch * hidden_size + batch * hidden_size + batch * hidden_size + batch * hidden_size * 8,综上所述,LSTM的计算量为:(embedding_size + hidden_size) * hidden_size * 4 个MACCembedding_size * hidden_size * 8 + hidden_size * (hidden_size + 20) 个FLOPS
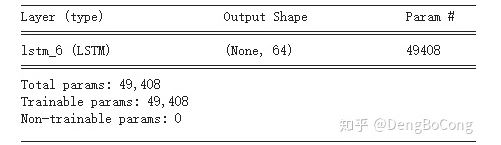
((embedding_size + hidden_size) * hidden_size + hidden_size) * 4对于特征维128的输入,LSTM单元数为64的网络来说,LSTM的参数量为:((128 + 64) * 64 + 64) * 4 = 49408,通过TensorFlow验证如下:
04
 的三维特征图,其中
的三维特征图,其中  是特征图的高度,
是特征图的高度,  是宽度,
是宽度,  是每个位置的通道数,正如我们所见今天使用的大多数卷积层都是二维正方内核,对于内核大小为
是每个位置的通道数,正如我们所见今天使用的大多数卷积层都是二维正方内核,对于内核大小为  的转换层,MACC的数量为:
的转换层,MACC的数量为:
输出特征图中有Hout × Wout × Cout个像素; 每个像素对应一个立体卷积核K x K x Cin在输入特征图上做立体卷积卷积出来的; 而这个立体卷积操作,卷积核上每个点都对应一次MACC操作
 ,128个filter的卷积,在
,128个filter的卷积,在  带有64个通道的输入特征图上,我们执行MACC的次数是:
带有64个通道的输入特征图上,我们执行MACC的次数是:
 ,以便输出特征图与输入特征图具有相同的大小。通常看到卷积层使用
,以便输出特征图与输入特征图具有相同的大小。通常看到卷积层使用  ,这会将输出特征图大小减少一半,在上面的计算中,我们将使用
,这会将输出特征图大小减少一半,在上面的计算中,我们将使用  而不是
而不是  。
。 ,128个filter的卷积,在
,128个filter的卷积,在  带有64个通道的输入特征图上的参数量为:
带有64个通道的输入特征图上的参数量为:  ,用TensorFlow验证结果如下图:
,用TensorFlow验证结果如下图: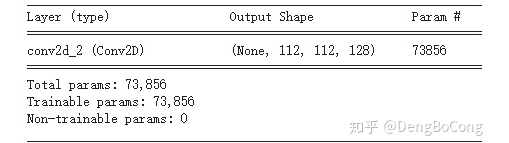
05

 的工作量,比常规的卷积层效率更高。当然,仅深度卷积是不够的,我们还需要增加“可分离”,第二个操作是常规卷积,但始终使用内核大小
的工作量,比常规的卷积层效率更高。当然,仅深度卷积是不够的,我们还需要增加“可分离”,第二个操作是常规卷积,但始终使用内核大小  ,即
,即  ,也称为“逐点”卷积,MACC的数量为:
,也称为“逐点”卷积,MACC的数量为:
 卷积进行比较:
卷积进行比较:3×3 depthwise : 7,225,3441×1 pointwise : 102,760,448深度可分离卷积 : 109,985,792 MACCs常规 3×3 卷积 : 924,844,032 MACCs

一个  卷积,为特征图添加更多通道(称为expansion layer)
卷积,为特征图添加更多通道(称为expansion layer) 深度卷积,用于过滤数据(depthwise convolution)
深度卷积,用于过滤数据(depthwise convolution) 卷积,再次减少通道数(projection layer,bottleneck convolution)
卷积,再次减少通道数(projection layer,bottleneck convolution)
 ,(参照上面传统卷积,把卷积核设置为1x1即得)
,(参照上面传统卷积,把卷积核设置为1x1即得) (参照MoblieNet V1分析)
(参照MoblieNet V1分析) (参照MoblieNet V1分析,或者传统卷积把卷积核设置为1x1即得)
(参照MoblieNet V1分析,或者传统卷积把卷积核设置为1x1即得)

 扩展因子6,以及
扩展因子6,以及  的
的  深度卷积和128输出通道,那么MACC的总数是:
深度卷积和128输出通道,那么MACC的总数是:
 卷积。但是......请注意,由于扩展层,在这个块内,我们实际上使用了
卷积。但是......请注意,由于扩展层,在这个块内,我们实际上使用了  通道。因此,这组层比原始的
通道。因此,这组层比原始的  卷积做得更多(从64到128个通道),而计算成本大致相同。
卷积做得更多(从64到128个通道),而计算成本大致相同。06

 是上一层的输出图中的元素。我们首先通过减去该输出通道的平均值并除以标准偏差来对该值进行归一化(epsilon 用于确保不除以0,通常为0.001),然后,我们将系数gamma缩放,然后添加一个偏差或偏移beta。每个通道都有自己的gamma,beta,均值和方差值,因此,如果卷积层的输出中有
是上一层的输出图中的元素。我们首先通过减去该输出通道的平均值并除以标准偏差来对该值进行归一化(epsilon 用于确保不除以0,通常为0.001),然后,我们将系数gamma缩放,然后添加一个偏差或偏移beta。每个通道都有自己的gamma,beta,均值和方差值,因此,如果卷积层的输出中有  个通道,则Batch normalization层将学习
个通道,则Batch normalization层将学习  参数,如下图所示:
参数,如下图所示:
07
 具有128通道的特征图上具有过滤器大小2和步幅2的最大池化层需要
具有128通道的特征图上具有过滤器大小2和步幅2的最大池化层需要  FLOPS或1.6兆FLOPS。当然,如果步幅与滤波器尺寸不同(例如
FLOPS或1.6兆FLOPS。当然,如果步幅与滤波器尺寸不同(例如  窗口,
窗口,  步幅),则这些数字会稍微改变。
步幅),则这些数字会稍微改变。08
减少参数 降低精度 融合计算单元步骤
https://www.jianshu.com/p/b8d48c99a47chttp://machinethink.net/blog/how-fast-is-my-model/http://colah.github.io/posts/2015-08-Understanding-LSTMs/https://datascience.stackexchange.com/questions/10615/number-of-parameters-in-an-lstm-modelhttps://zhuanlan.zhihu.com/p/77471991https://arxiv.org/abs/1506.02626
猜您喜欢:
附下载 |《TensorFlow 2.0 深度学习算法实战》
