堆和堆傻傻分不清?一文告诉你 Java 集合中「堆」的最佳打开方式
什么是堆?
堆其实就是一种特殊的队列——优先队列。
普通的队列游戏规则很简单:就是先进先出;但这种优先队列搞特殊,不是按照进队列的时间顺序,而是按照每个元素的优先级来比拼,优先级高的在堆顶。
这也很容易理解吧,比如各种软件都有会员制度,某软件用了会员就能加速下载的,不同等级的会员速度还不一样,那就是优先级不同呀。
还有其实每个人回复微信消息也是默默的把消息放进堆里排个序:先回男朋友女朋友的,然后再回其他人的。
这里要区别于操作系统里的那个“堆”,这两个虽然都叫堆,但是没有半毛钱关系,都是借用了 Heap 这个英文单词而已。
我们再来回顾一下「堆」在整个 Java 集合框架中的位置:
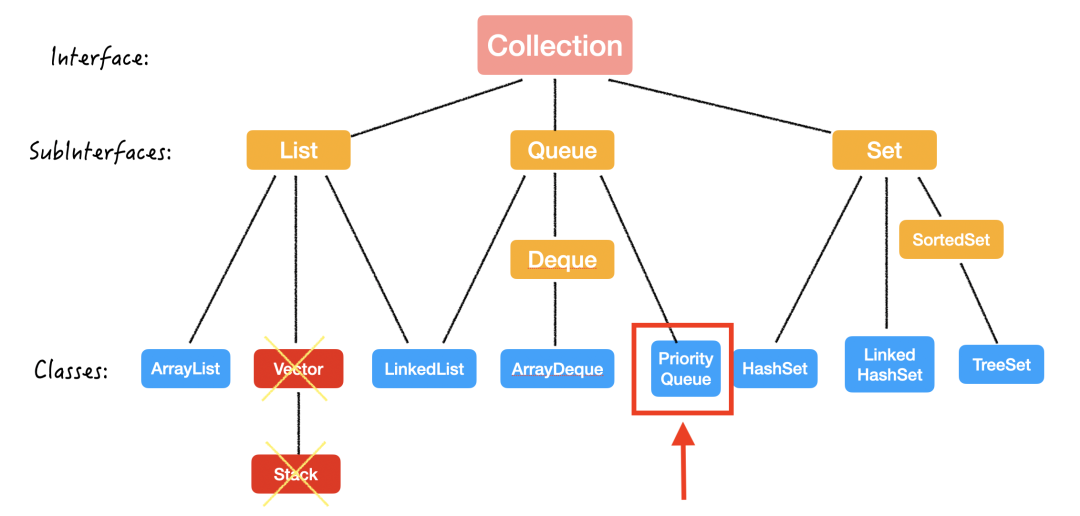
也就是说,
PriorityQueue 是一个类 (class);
PriorityQueue 继承自 Queue 这个接口 (Interface);
堆的特点
堆是一棵完全二叉树; 堆序性 (heap order): 任意节点都优于它的所有孩子。 a. 如果是任意节点都大于它的所有孩子,这样的堆叫大顶堆,Max Heap; b. 如果是任意节点都小于它的所有孩子,这样的堆叫小顶堆,Min Heap;
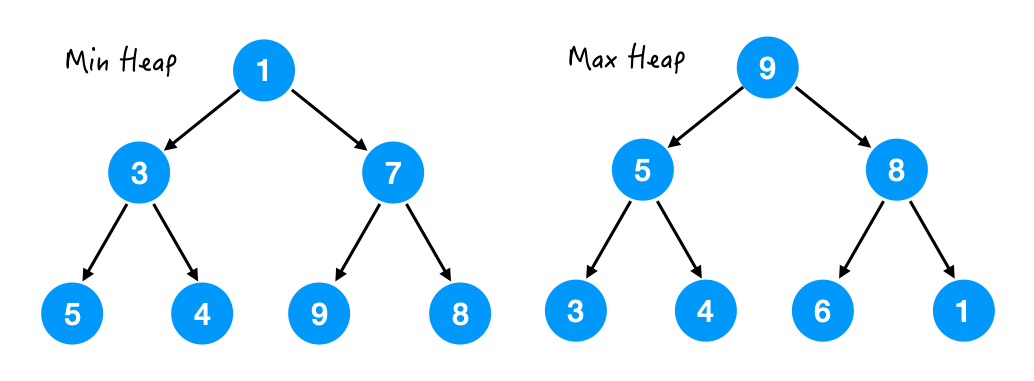
既然堆是用数组来实现的,那么我们可以找到每个节点和它的父母/孩子之间的关系,从而可以直接访问到它们。
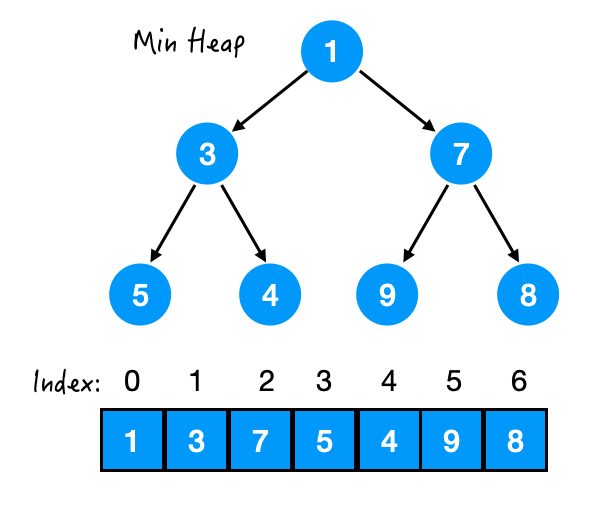
它的 Index = 1, 它的 parent index = 0, 左孩子 left child index = 3, 右孩子 right child index = 4.
设当前节点的 index = x, 那么 parent index = (x-1)/2, 左孩子 left child index = 2*x + 1, 右孩子 right child index = 2*x + 2.
基本操作
| 功能 | 方法 | 时间复杂度 |
|---|---|---|
| 增 | offer(E e) | O(logn) |
| 删 | poll() | O(logn) |
| 改 | 无直接的 API | 删 + 增 |
| 查 | peek() | O(1) |
peek() 的时间复杂度很好理解,因为堆的用途就是能够快速的拿到一组数据里的最大/最小值,所以这一步的时间复杂度一定是 O(1) 的,这就是堆的意义所在。offer(E e) 和 poll() 的过程。offer(E e)
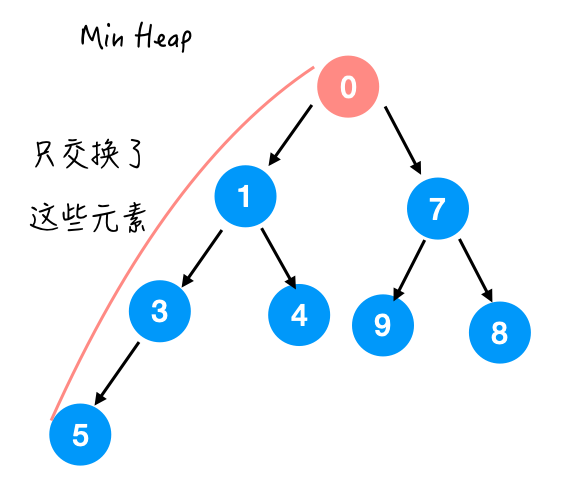
0 到刚才这个最小堆里面: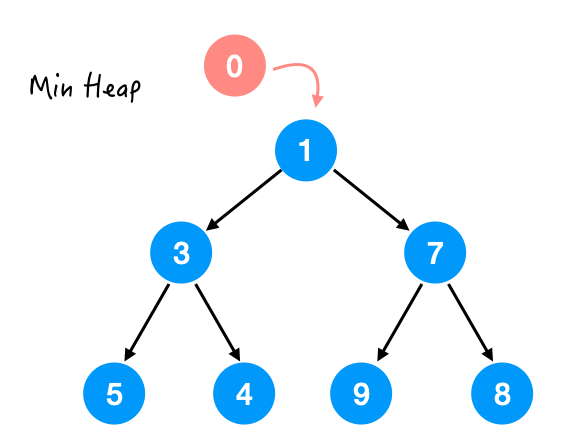
我们先保证加了元素之后这棵树还是一棵完全二叉树, 然后再通过 swap 的方式进行微调,来满足堆序性。
Step 1.
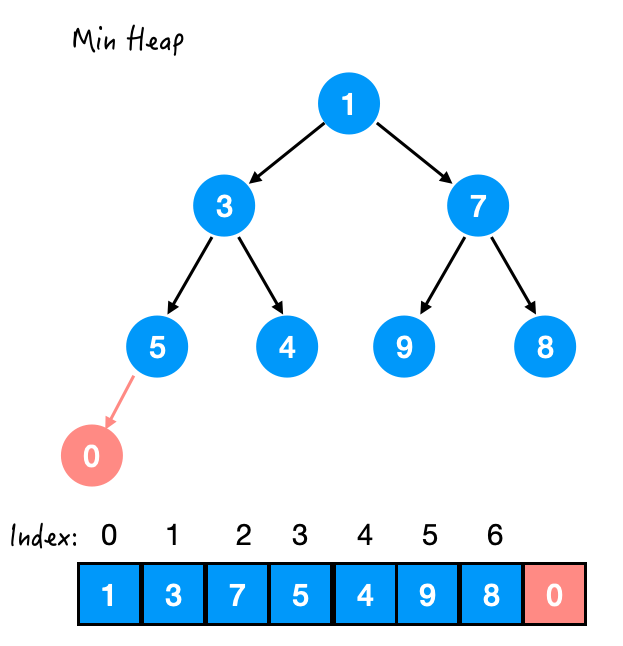
是否满足堆序性。
Step 2. 与 5 交换
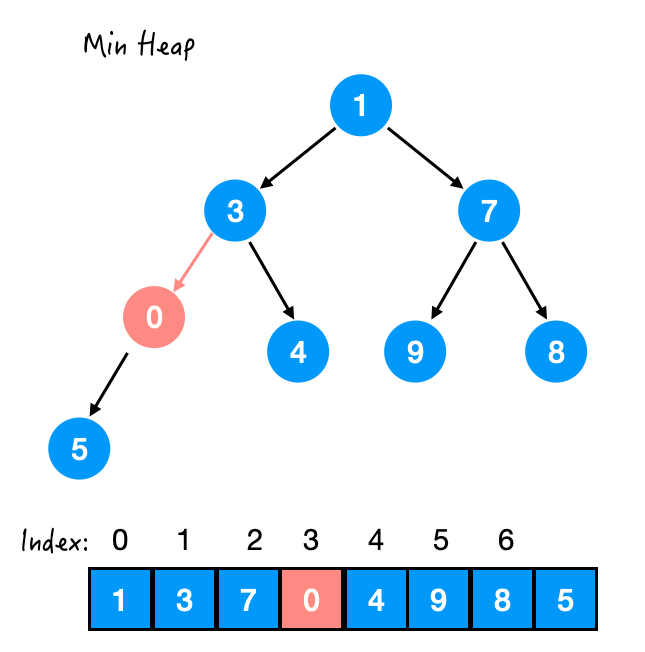
Step 3. 与 3 交换
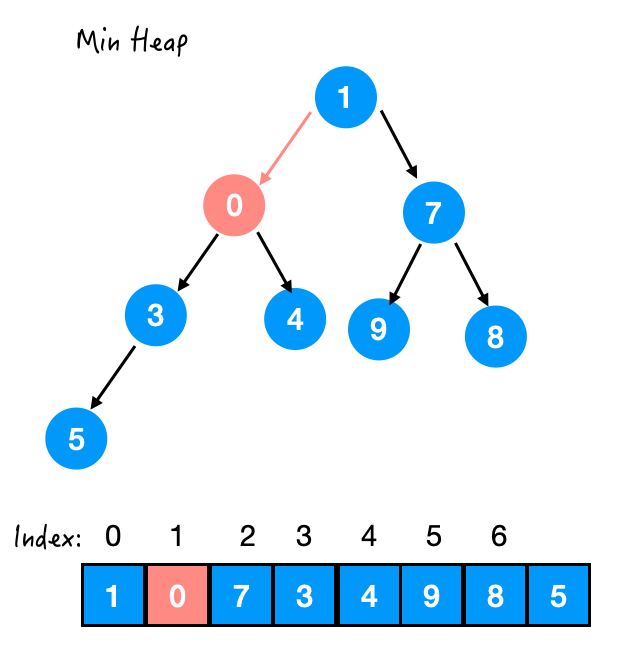
Step 4. 与 1 交换
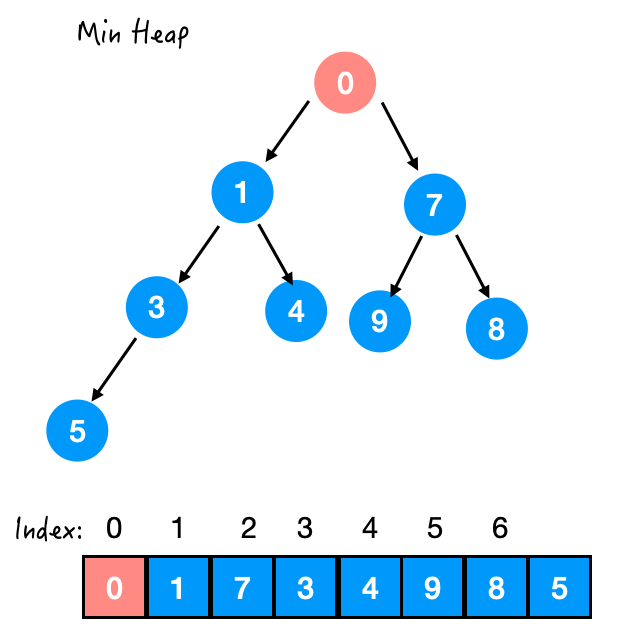
siftUp(),源码如下:
时间复杂度
O(height) 次。O(height) = O(logn)。offer(E e) 的时间复杂度就是 O(logn) 啦。poll()
poll() 就是把最顶端的元素拿走。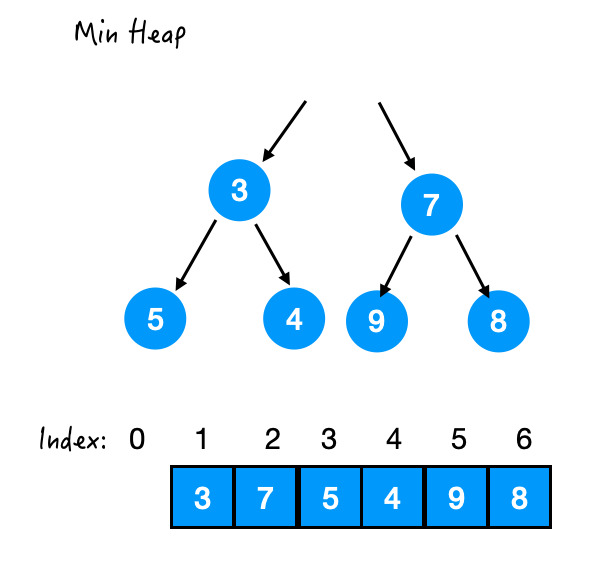
Step1. 末尾元素上位
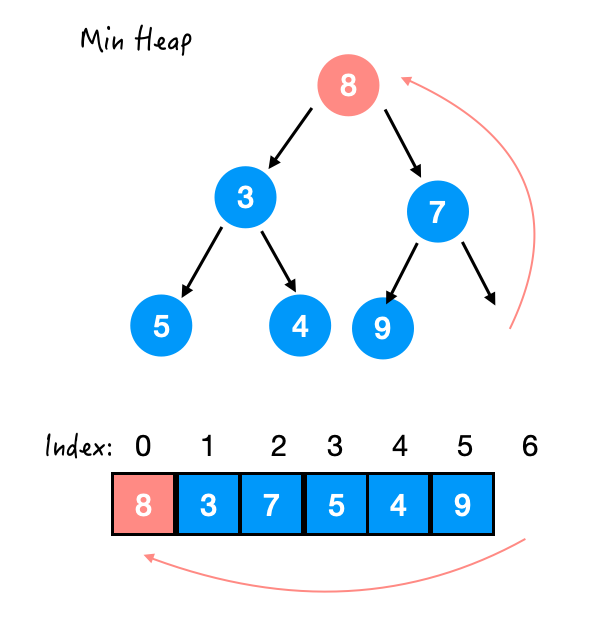
Step 2. 与 3 交换
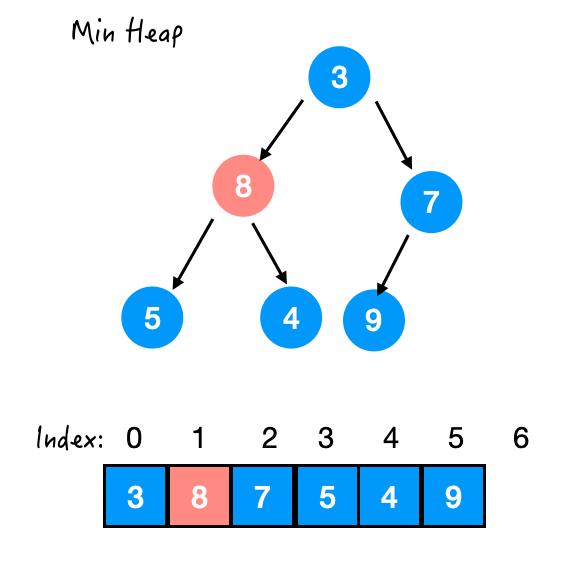
Step 3. 与 4 交换
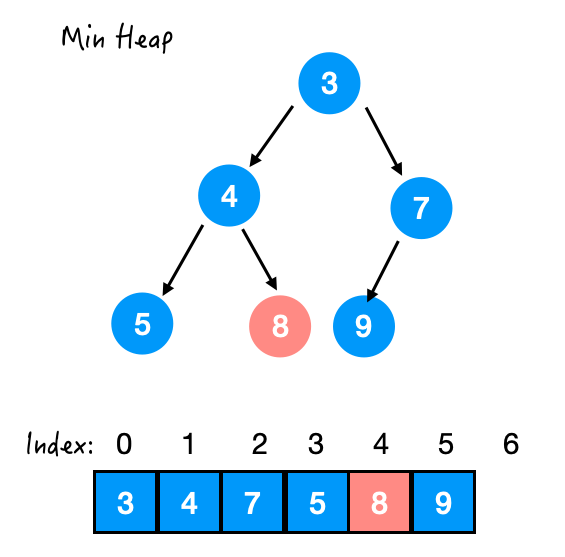
siftDown(),源码如下:
时间复杂度
O(height) 次。offer(E e) 的时间复杂度就是 O(logn) 啦。heapify()
heapify() 了,它是一个很神奇的操作,可以用 O(n) 的时间把一个乱序的数组变成一个 heap。
heapify() 并不是一个 public API,看:
heapify() 的方式呢,就是使用PriorityQueue(Collection c)从最后一个非叶子节点开始,从后往前做 siftDown().
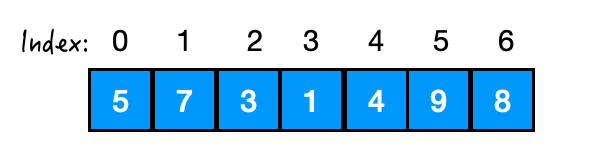
heapify() 操作,想把它变成一个最小堆,拿到它的最小值。siftDown().Step 1.
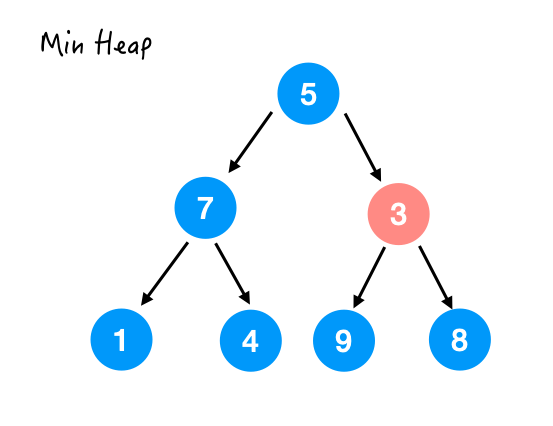
Step 2.
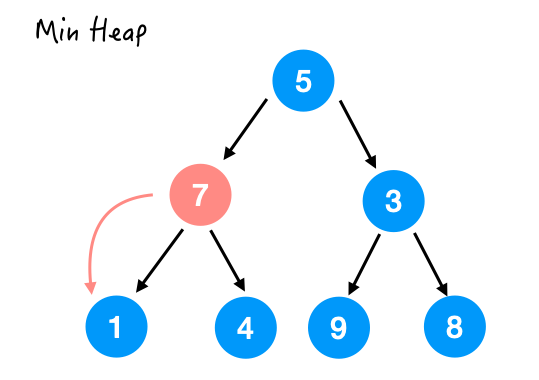
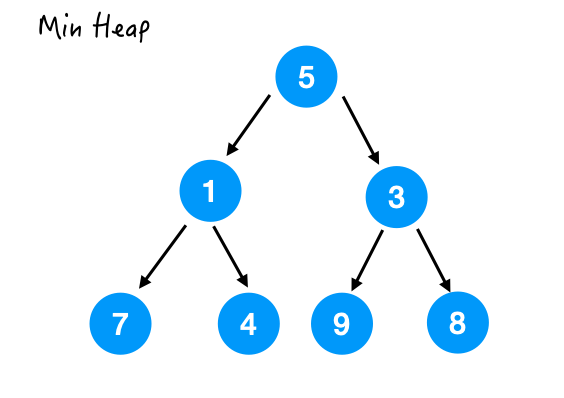
Step 3.
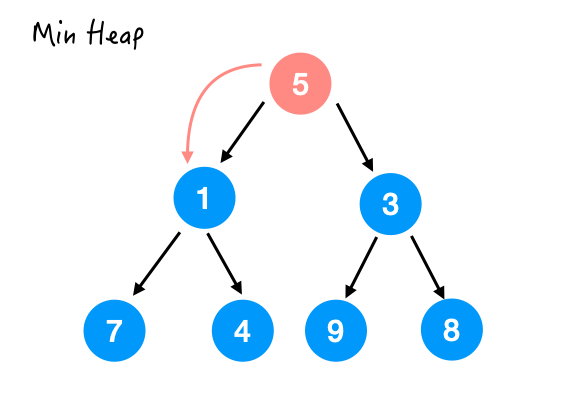
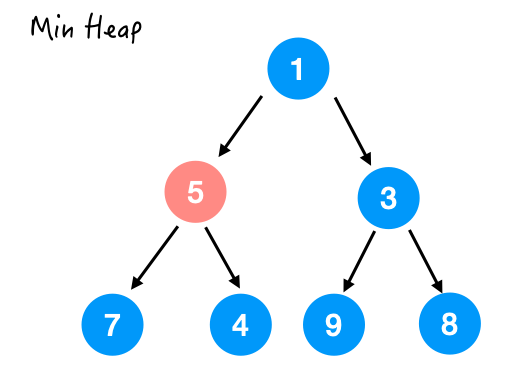
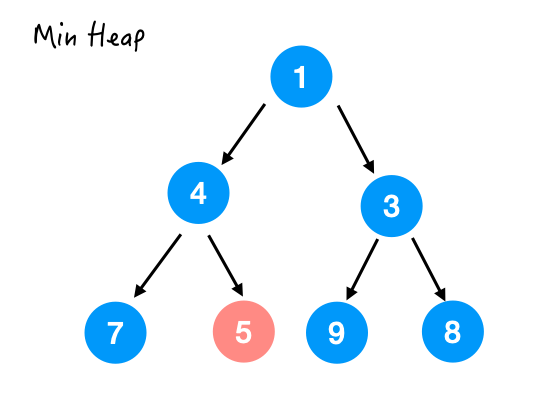
heapify() 的过程就完成了。好了难点来了,为什么时间复杂度是 O(n) 的呢?
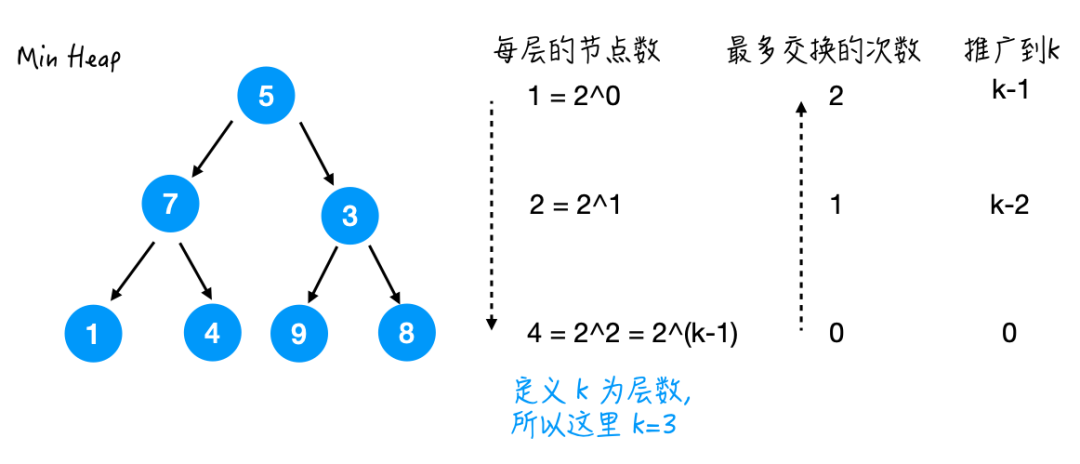
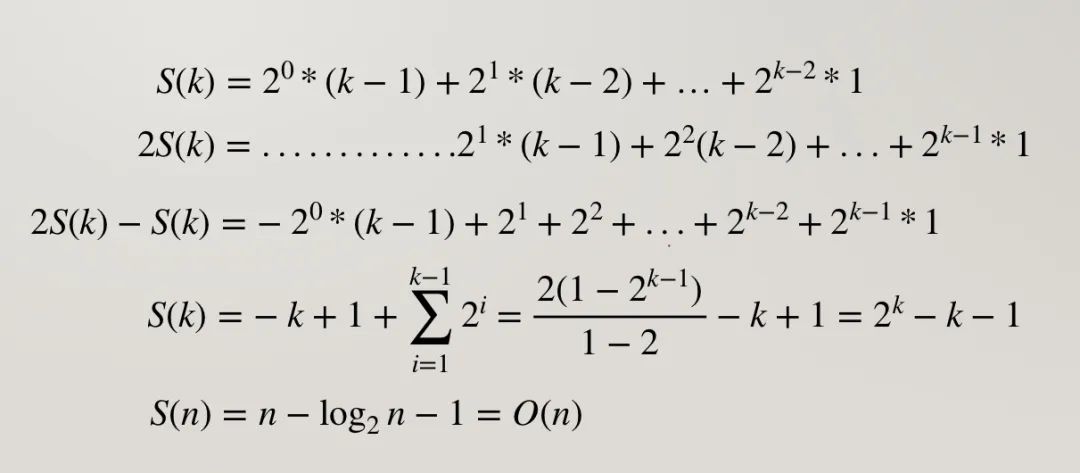
heapify() 时间复杂度是 O(n).heapify() 虽然不能直接操作,但是堆排序中用到了这种思路。有道无术,术可成;有术无道,止于术
欢迎大家关注Java之道公众号
好文章,我在看❤️
评论
