教你一步步从统计学开始入手数据分析!
统计学是在数据分析的基础上,研究如何测定、收集、整理、归纳和分析反映数据数据,以便给出正确消息的科学。如果要学习数据分析,那么扎实的统计知识是必备的。
本文参考《深入浅出统计学》二 、三、 四、 五 章知识,对重点内容进行归纳总结。最后有几个统计概率应用的例子以及使用python分析6家上市公司股票的干货。
1
统计学基础
1.均值
平均数的一般量度:
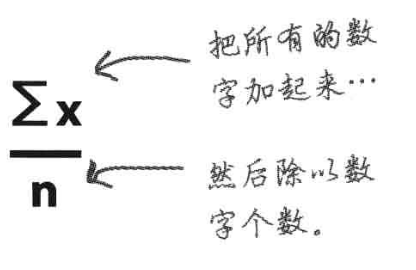
均值公式
有时候一些数据重复了,这时候需要用到频数:
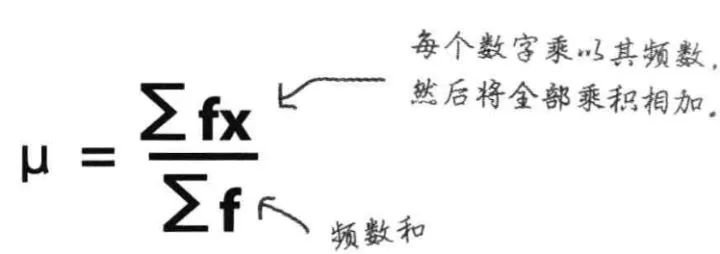 频数公式
频数公式
2.中位数
偏斜数据和异常值使均值误导的时候,用它,它是中间值。
3.众数
数据中出现最多的数值。
4.四分数
四分位数(Quartile)是统计学中分位数的一种,即把所有数值由小到大排列并分成四等份,处于三个分割点位置的數值就是四分位数。
注意:由小到大排列。
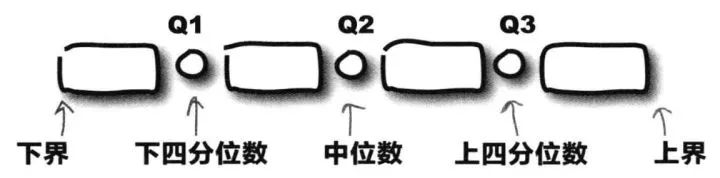
四分位数
第一四分位数 (Q1):又称“较小四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。
第二四分位数 (Q2):又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。
第三四分位数 (Q3):又称“较大四分位数”,等于该样本中所有数值由小到大排列后第75%的数字
第三四分位数与第一四分位数的差距又称四分位距(InterQuartile Range, IQR)。
5.方差
(variance)统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。
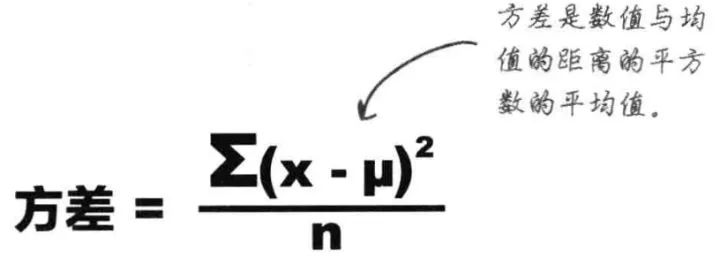
方差
6.标准差(Standard deviation)
离均差平方的算术平均数的平方根,用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据,标准差未必相同。
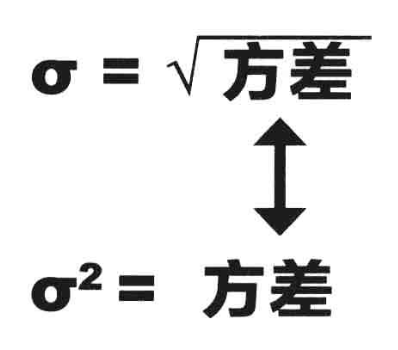
标准差
方差所得的数值之平方根就是总体的标准偏差。
7.标准分
是一种由原始分推导出来的相对地位量数,它是用来说明原始分在所属的那批分数中的相对位置的。

标准分
2
概率计算
概率是对随机事件发生的可能性的度量,一般以一个在0到1之间的实数表示一个事件发生的可能性大小。

概率
1.对立事件
若A交B为不可能事件,A并B为必然事件,那么称A事件与事件B互为对立事件,其含义是:事件A和事件B必有一个且仅有一个发生。
对立事件概率之间的关系:P(A)+P(B)=1。
例如:在掷骰子试验中,A={出现的点数为偶数},b={出现的点数为奇数},A∩B为不可能事件,A∪B为必然事件,所以A与B互为对立事件。
2.相交事件
有可能同时发生的两件事。
相交事件
3.互斥事件
两件事中只可能发生一件。
抛硬币,正反面是互斥,抛出正面就不可能有反面。
4.独立事件
发生概率不受其他事件影响。
你抛一个硬币三次,结果全是"正面"……下一次抛掷的结果也是"正面"的可能性是多少?
可能性是 ½(0.5),和任何一次抛掷一样。
以前的抛掷不会影响这次抛掷!

贝叶斯定理(英语:Bayes' theorem)是概率论中的一个定理,它跟随机变量的条件概率以及边缘概率分布有关。在有些关于概率的解释中,贝叶斯定理(贝叶斯公式)能够告知我们如何利用新证据修改已有的看法。這個名稱來自於托马斯·贝叶斯。
在介绍贝叶斯定理之前,先简单地介绍一下条件概率,描述的是事件 A 在另一个事件 B 已经发生条件下的概率,记作P(A|B), A 和 B 可能是相互独立的两个事件,也可能不是:

3
概率统计的应用
1.期望值
在概率论和统计学中,一个离散性随机变量的期望值(或数学期望、或均值,亦简称期望,物理学中称为期待值)是试验中每次可能的结果乘以其结果概率的总和。


2.夏普比率
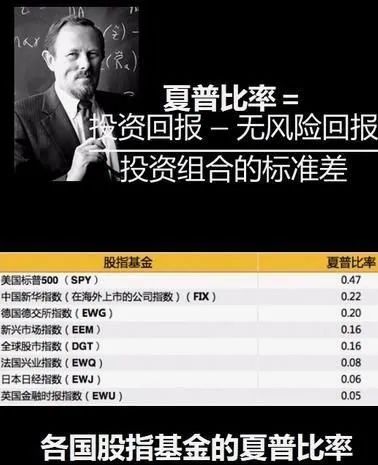
现代投资理论的研究表明,风险的大小在决定组合的表现上具有基础性的作用。风险调整后的收益率就是一个可以同时对收益与风险加以考虑的综合指标,以期能够排除风险因素对绩效评估的不利影响。夏普比率就是一个可以同时对收益与风险加以综合考虑的三大经典指标之一。
如果夏普比率为正值,说明在衡量期内基金的平均净值增长率超过了无风险利率,在以同期银行存款利率作为无风险利率的情况下,说明投资基金比银行存款要好。夏普比率越大,说明基金的单位风险所获得的风险回报越高。夏普比率为负时,按大小排序没有意义。[1] 夏普比率以资本市场线作为评价基准,对投资绩效作出评估。
3.利用Python分析6家公司股票(阿里巴巴 亚马逊 腾讯 苹果 facebook 谷歌)
首先导入包

创建字典

获取阿里巴巴股票数据


会得到如下股票数据:

查看数据集描述

会得到下面的数据:
分析涨跌得到如下数据:


绘图步骤


可以得到‘阿里巴巴’的股票走向
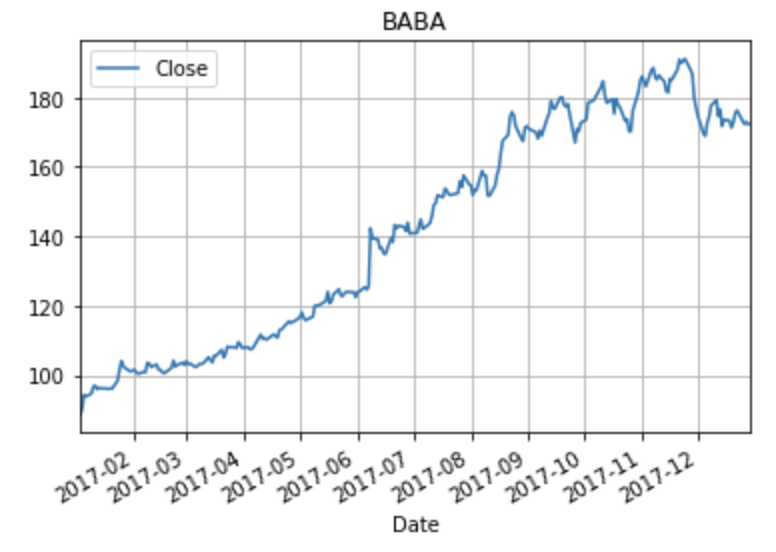
其他几家公司同理:





