每日一道 LeetCode (54):电话号码的字母组合

❝每天 3 分钟,走上算法的逆袭之路。
❞
前文合集
代码仓库
GitHub:https://github.com/meteor1993/LeetCode
Gitee:https://gitee.com/inwsy/LeetCode
题目:电话号码的字母组合
难度:「中等」
题目来源:https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
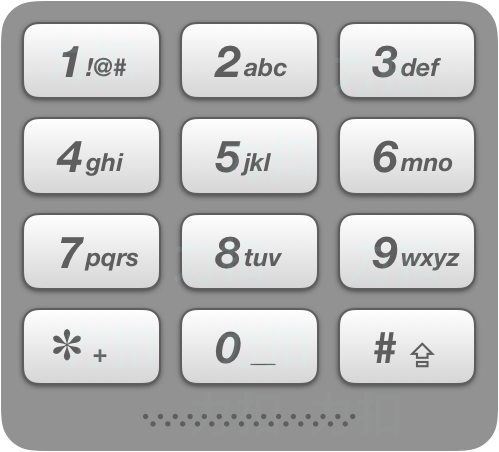
示例:
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明: 尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
解题思路
这道题看着有木有感觉很简单的样子,至少我一开始是觉得蛮简单的。
先使用哈希表定义一个字典:
static final Map map = Map.of(
'2', "abc", '3', "def", '4', "ghi", '5', "jkl",
'6', "mno", '7', "pqrs", '8', "tuv", '9', "wxyz"
);
上面这个是在 JDK9 以后开始支持的初始化方式,正好 LeetCode 也支持 JDK9 的语法,如果一定要用 JDK8 的话,emmmmmmmm:
Map map = new HashMap() {{
put('2', "abc");
put('3', "def");
put('4', "ghi");
put('5', "jkl");
put('6', "mno");
put('7', "pqrs");
put('8', "tuv");
put('9', "wxyz");
}};
别问我为啥要用 JDK9 的写法,问就是省纸。
接下来思考那个示例 「23」 ,首先程序先解析 2 , 2 对应了三个字母 abc , 3 也对应了三个字母 def ,这道题在最终输出的结果集没玩什么滑头,直接就是所有的情况都排列出来就可以了,那么我可以套两个循环,直接把所有的情况全都迭代出来。

但是题目上并没有说输入的字符串一定是两位的,如果是三位的那不就傻了。实际上是输出的字符串有几位就需要套几层循环,好像不是很好写啊。。。
这个时候,就需要用到一种不是很好理解,并且不是很好写的方案了——递归。
使用递归的时候并不需要指定递归的次数,递归是直接递归到底的。
于是就有了下面这段代码:
// 最终结果
private List res = new ArrayList<> ();
// 组合形式
private StringBuilder sb = new StringBuilder();
public List letterCombinations(String digits) {
if (digits.length() == 0) return res;
backtrack(digits, 0);
return res;
}
// 回溯函数
public void backtrack(String digits, int index) {
if (index == digits.length()) {
res.add(sb.toString());
} else {
char digit = digits.charAt(index);
String letters = map.get(digit);
int lettersCount = letters.length();
for (int i = 0; i < lettersCount; i++) {
sb.append(letters.charAt(i));
backtrack(digits, index + 1);
sb.deleteCharAt(sb.length() - 1);
}
}
}
整段代码并不长,而且看起来还很好理解,整体最核心的就是在那个 for 循环里面的三句话:
sb.append(letters.charAt(i));
backtrack(digits, index + 1);
sb.deleteCharAt(sb.length() - 1);
第一句话是先把当前的值放入到我们的全局对象 sb 中,按照案例的 「23」 来演示的话就是先把 a 放到 sb 中,然后开始递归进下一次,这时候,我们第一个字符串全都是 a ,第二个字符串 3 对应的可选值有 def ,接着我们把 d 也放到 sb 中,这时 sb 中的值是 ad ,然后进入下一次迭代,走到上面的那个判断,把 sb 中的 ad 放入最终的输出结果 res 中,然后递归往上走一层,删除 sb 中的最后一个数,这时 sb 中剩下的是 a , for 循环进入下一次循环 ,像 sb 中添加一个 e ,然后重复上面的过程。
上面这段解释有点绕,可以多读几次,或者在代码上多打几个断点手动 debug 一下,分分钟就懂了。

