心中有“树”！图文并茂介绍数据结构中常见的树（一）-技术圈

提到数据结构中的树（Tree) ，大家应该都不陌生，相关书籍中都有大段篇幅的介绍，刷 Leetcode 的时候会遇到很多相关问题。很多人往往会用 “手写红黑树” 来形容面试难度很高。

那么，除了红黑树之外，还有哪些常见的树结构？它们被用在什么领域？又解决了什么问题？接下来，我们就用几篇文章，来给大家做一个简单的介绍。

大家好，我是不会写代码的纯序员——Chunel Feng。各位绅士们，很高兴我们又在这里见面了。

刷 leetcode 的童鞋，肯定写过二叉树的遍历、递归、查询等逻辑，笔试的时候 6 的飞起，人均 sp。但很多童鞋可能也会有这样一种感觉：这些东西只能应付面试，不实用，工作了好好几年了，根本没用过。

其实，我们在工作中接触到的很多东西，底层的本质就是一棵树型结构，只是有前人为我们造好了屏蔽实现细节的轮子，才让我们的工作变得如此丝滑。举两个常见的例子：C++里的 std::set 和 std::map 结构，底层就是一颗树；常见的数据库存储引擎，底层也是树型结构。

那么，常用的数据结构里还有哪些常见树呢？它们又会被应用在哪里？用于解决什么样的问题？ 下面，我们就从以上几个问题入手，来介绍一下我所知道的一些 Tree 方面的知识，希望对大家有所帮助。

在开始之前，首先说明，本文偏科普和综述，并不会对每种树做非常详细的介绍，也不会上什么类似红黑树旋转的代码。主要目的是让大家知道有这些内容，如果今后有需要用到的地方，自己查缺补漏即可。本人水平有限，如果有描述的错误或遗漏，也欢迎大家随时补充和交流。

下面我们正式开始：

二叉树

BST 搜索二叉树 Binary Search Tree

树，最常见的用法，就是用于数值查找。通过在建树的时候，将大于 root 的值放到右边、小于 root 的值放到左边，即可在查询的时候，减少比较次数，实现加速查询。

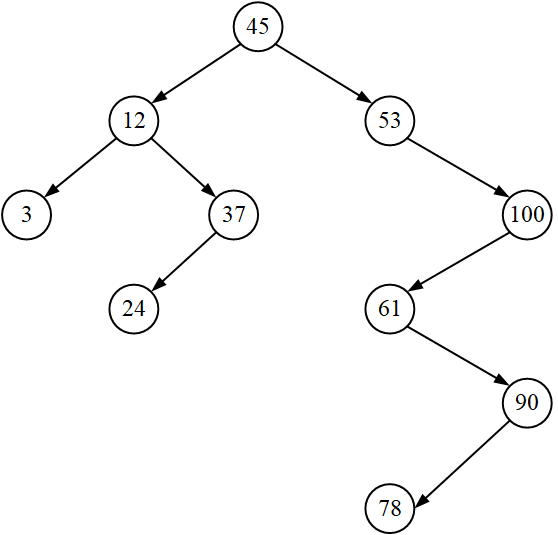
但是，随着数据的插入越来越多，树的结构会造成扭曲（不平衡）。比如，往 bst 中插入一个递增数组的时候，普通的 BST 会退化成一个链表，从而严重影响查询性能。

AVL 平衡二叉树 Height-Balanced Binary Search Tree

于是，AVL 平衡二叉树诞生了。AVL 的名字，取自于作者 Adelson-Velskii 和 Landis 的首字母缩写（纯序员暗自感慨，如果是第一位作者独立发明的话，那数据结构课上就又多了个话题）。

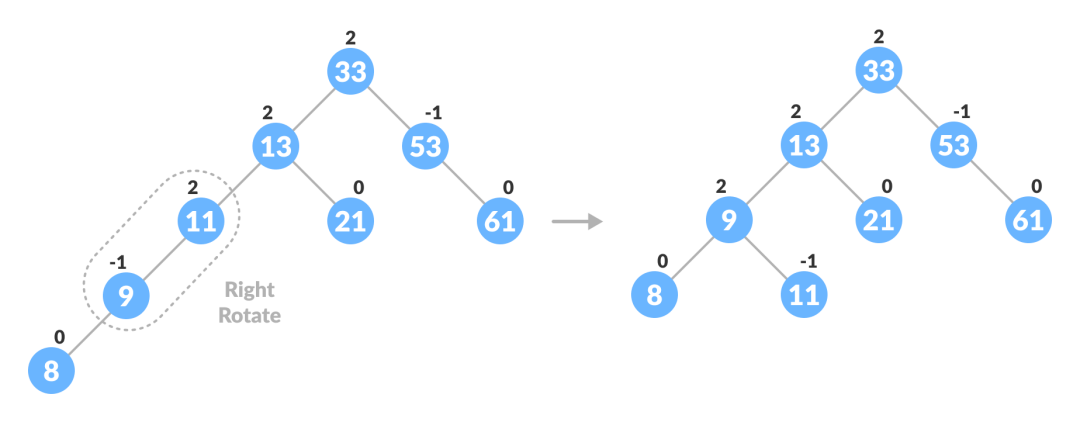
AVL 树通过在插入过程中的旋转逻辑，使得树的自身高度差严格控制在 1 之内，从而解决了退化成 list 的问题。但是，频繁的旋转增加了树构建的成本。

RBT 红黑树 Red Black Tree

为了降低树构建时的成本，红黑树诞生了。红黑树通过将节点设定成 Red or Black，和同一条边中 Black 节点的数量相同等约束条件，在保证了树基本平衡的情况下，优化了自旋转流程。

红黑树可以有效的平衡建树时的旋转次数和查找时的退化问题，并且也在实际编程中得到了广泛的应用。比如 C++中的 std::map 和 Java 里的 TreeMap 的底层就是一颗红黑树，nginx 和 epoll 源码中也有所使用。

字典树

Trie 前缀树

Trie 树是常见的字典树，通常被用于字符串查询和排序。它的形式，是在根节点的所有路径中，有序的依次存入一个对应字符。这样做，一方面可以降低海量字符串存储所占用的空间，另一方面也使得字符串得以有序的排列，同时也可以记录重复出现次数。

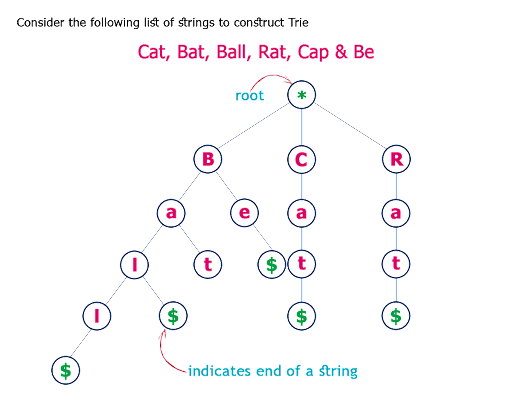
这算是搜索引擎里最最最简单的样例吧，记住哦，面试中经常问的。想继续往搜索引擎方面了解一些的童鞋，可以看一下 FST（Finite State Transducers，有限状态转移机），这个就不属于【树】的范畴了，我们不在这里讨论了。

Radix 压缩前缀树，也叫基数树

样子跟前面提到的 Trie 树有点相似。相比于 Trie 中一个一个往下追加的流程，Radix 在插入的时候通过分裂机制使得仅包含一条链路的字符【压缩】到一起。从而在保持原有查询、排序功能的前提下，进一步降低了数据的存储占用量。顺便说一句，Radix 树中的节点，还适合用于存放类似 .*? 这种正则匹配相关的信息。

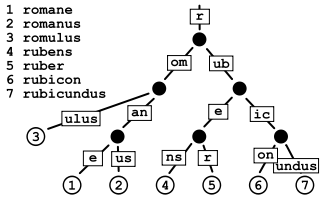
一图胜千言，看到上面这个图，我想大家应该都懂了。Radix 树有一个常见的应用，就是文件路径查找或匹配，这一点做前后端交互的朋友应该有所涉及。

/usr/local/include/         (14KB)/usr/local/bin/             (25KB)/usr/study/book/            (3MB)/usr/study/.video/          (380GB)...

比如，我电脑中的文件夹分类吧，用 Radix 树存储的话，就比 Trie 节省了很多空间，因为 /usr，/local，/study这几个信息，明显是可以合并到一个节点中的。

Suffix tree 后缀树

上面聊到的两种字典树，都属于前缀树，其实还有后缀树。后缀树是对一个长字符串的详尽描述（注意，是一个 string 对应一棵后缀树，不是海量 string 放到一棵树上）。树的每条路径记录了一个后缀信息，后缀下标用于记录从第 x 个字符开始计算，从而简化的查询流程。主要用途有：字符串匹配，查找最长公共子串，查找最长重复子串等。

这个讲起来有点复杂，有兴趣的朋友可以去 B 站搜索：轻松掌握 suffix tree^[1] ，讲的非常通俗易懂，墙裂推荐。

本章小节

本章是这个系列的第一篇内容，主要是聊了我写这个系列的文章的出发点和目的，也简单介绍了几种类型的树，并梳理了他们的使用场景和异同，希望对大家有所帮助。

在这个系列接下来的几篇文章中，我们还会继续给大家介绍一些常见的树结构，比如lsm 树，kd 树、哈夫曼树等等。也希望对类似话题感兴趣的朋友，可以加我微信，一起讨论和交流相关的内容。

引用链接

[1] 轻松掌握 suffix tree: https://www.bilibili.com/video/BV1c741137GD?spm_id_from=333.999.0.0

长按识别下图二维码，关注公众号「Doocs 开源社区」，第一时间跟你们分享好玩、实用的技术文章与业内最新资讯。