给定一个二叉树，如何判断它是对称的

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

    1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3

进阶：

你可以运用递归和迭代两种方法解决这个问题吗？

解答：

一棵二叉树对称，则需要满足：根的左右子树是镜像对称的

也就是说，每棵树的左子树都和另外一颗树的右子树镜像对称，左子树的根节点值与右子树的根节点值相等

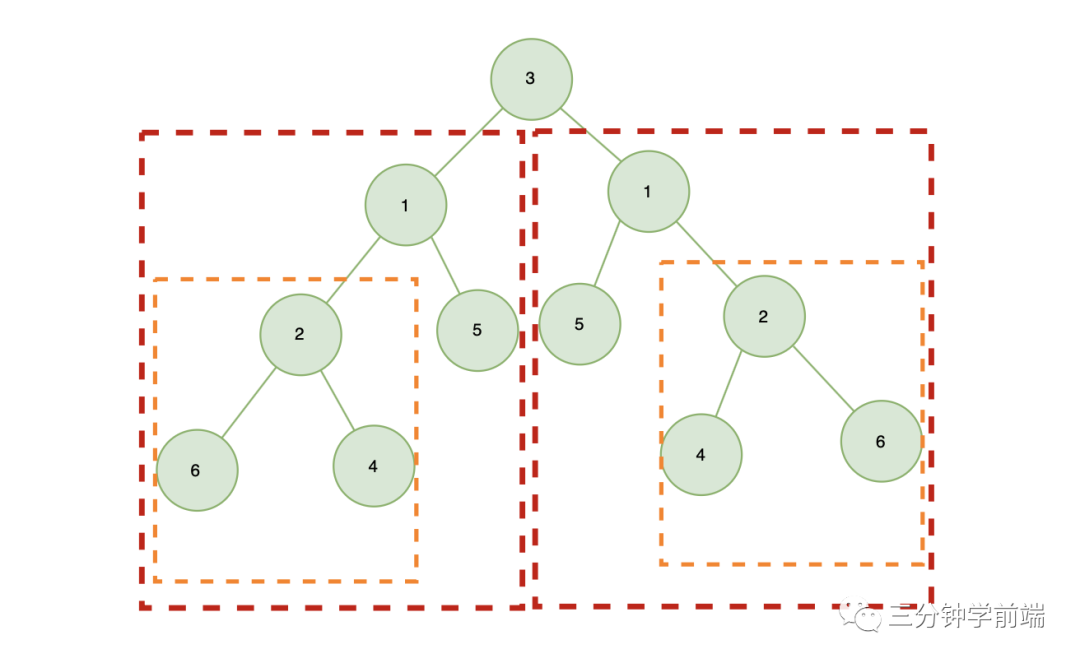
所以，我们需要比较：

• 左右子树的根节点值是否相等
• 左右子树是否镜像对称

边界条件：

• 左右子树都为 null 时，返回 true
• 左右子树有一个 null 时，返回 false

解法一：递归

const isSymmetric = function(root) {
    if(!root) return true
    var isEqual = function(left, right) {
        if(!left && !right) return true
        if(!left || !right) return false
        return left.val === right.val
         && isEqual(left.left, right.right)
         && isEqual(left.right, right.left)
    }
    return isEqual(root.left, root.right)
};

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

解法二：迭代

利用栈来记录比较的过程，实际上，递归就使用了调用栈，所以这里我们可以使用栈来模拟递归的过程

• 首先根的左右子树入栈
• 将左右子树出栈，比较两个数是否互为镜像
• 如果左右子树的根节点值相等，则将左子树的 left 、右子树的 right 、左子树的 right 、右子树的 left 依次入栈
• 继续出栈（一次出栈两个进行比较）…….

依次循环出栈入栈，直到栈为空

const isSymmetric = function(root) {
    if(!root) return true
    let stack = [root.left, root.right]
    while(stack.length) {
        let right = stack.pop()
        let left = stack.pop()
        if(left && right) {
            if(left.val !== right.val) return false
            stack.push(left.left)
            stack.push(right.right)
            stack.push(left.right)
            stack.push(right.left)
        } else if(left || right) {
            return false
        }
    }
    return true
};

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)