面测开不会手写二叉树遍历?被大厂教育……
近年来各大厂对测试的招聘要求越来越严格,大部分都计划或正在将团队换血成既具有开发能力又有测试敏感度的测试开发工程师,所以手写算法这种考察开发能力的手段也经常在测开的面试中出现了,曾经单纯的以为不会出太难的吧,考察基础的数组、字符串、递归、排序可能就OK了吧,像什么树啊、链表、图之类的的面试测开应该不会出吧,所以平时一般直接跳过那些……直到最近遇到了某大厂让手写二叉树的非递归遍历,然后就知道了还是太naive,欠的技术债终究还是要还的……今天就把二叉树的相关知识好好归纳一下,然后再编码实现一个二叉树的前序遍历。

什么是树?
树是数据结构中比较重要也是比较难理解的一类存储结构,因为我们通常对线性储存结构比较熟悉,而数是一种非线性存储结构,如下图:
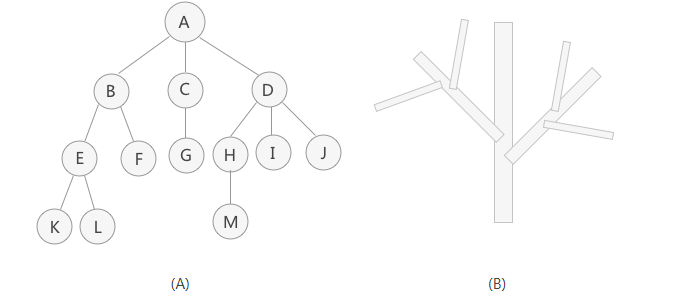
二叉树
二叉树是一种比较特殊的树形结构,需要满足下面2个条件:
1、本身是一个有序树;
2、树中包含的各个节点的子节点数都不能超过 2,即只能是 0、1 或者 2;
如下图所示:
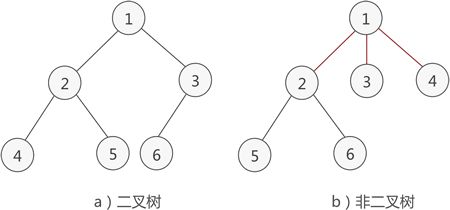
PS:其中没有子节点的节点被叫做叶子节点。
下面再了解2个特殊的二叉树:
1、满二叉树
如果二叉树中除了叶子结点,其他结点的子节点数都为 2,则此二叉树称为满二叉树。如下图:
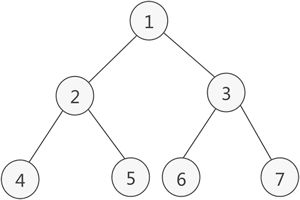
2、完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。如下图:
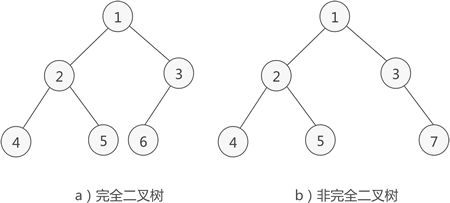
二叉树如何存储?
前面了解了二叉树的结构,对与这样的非线性结构,在程序设计时要如何存储?
1、二叉树的顺序存储结构
二叉树的顺序存储,指的是使用数组来存储二叉树,但是这只能是对于完全二叉树,因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。这一部分我们就简单的用个例子来说明下:
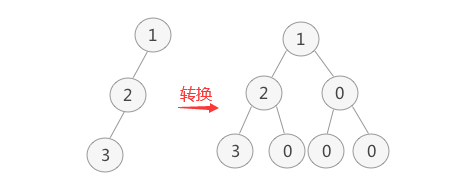
完全二叉树,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。那么上图的二叉树存入数组就是这样的:

2、二叉树的链式存储结构
仔细观察你会发现,其实二叉树并不适合用数组来存储,普通二叉树转换成完全二叉树才能存储到数组中,但是转换过程中补齐的那些“无用”节点就浪费了数组的存储空间。所以推荐使用链式存储,只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可,如下图:
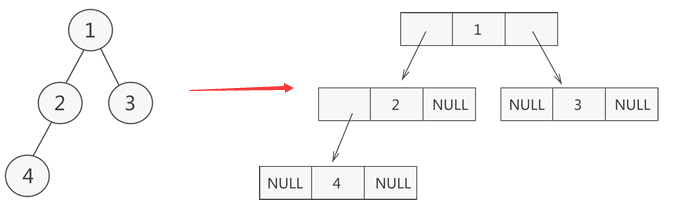
这样节点就必须包含下列数据信息:
指向左孩子节点的指针(Lchild);
节点存储的数据(data);
指向右孩子节点的指针(Rchild);
生成一颗二叉树
现在我们就来定义二叉树的节点,非常简单,直接定义节点需要包含的信息数据和左右孩子信息即可,那么我们直接上代码:
class TreeNode {
public int value;
public TreeNode left;
public TreeNode right;
public TreeNode(int _value) {
value = _value;
}
}
节点定义好了,那么我们如何才生成一棵二叉树呢?可以参考定义二叉树的特性和条件:是有序的,且树中包含的各个节点的子节点数都不能超过 2。下面以数组形式生成一棵完全二叉树,代码实现如下:
TreeNode[] node = new TreeNode[10];
for(int i = 0; i < 10; i++) { //先顺序赋值,保证有序
node[i] = new TreeNode(i);
}
for(int i = 0; i < 10; i++) {
if(i*2+1 < 10) //左孩子
node[i].left = node[i*2+1];
if(i*2+2 < 10) //右孩子
node[i].right = node[i*2+2];
}
二叉树的前序遍历
前序遍历又叫先序遍历,前序遍历的逻辑是:首先访问根结点然后遍历左子树,最后遍历右子树,简称:根左右。
比如下面这棵二叉树,前序遍历的路径结果就是:1->2->4->5->3->6->7
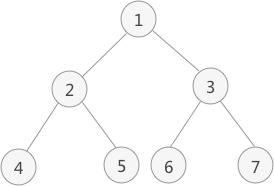
遍历该二叉树的过程为:
访问该二叉树的根节点,找到 1;
访问节点 1 的左子树,找到节点 2;
访问节点 2 的左子树,找到节点 4;
由于访问节点 4 左子树失败,且也没有右子树,因此以节点 4 为根节点的子树遍历完成。但节点 2 还没有遍历其右子树,因此现在开始遍历,即访问节点 5;
由于节点 5 无左右子树,因此节点 5 遍历完成,并且由此以节点 2 为根节点的子树也遍历完成。现在回到节点 1 ,并开始遍历该节点的右子树,即访问节点 3;
访问节点 3 左子树,找到节点 6;
由于节点 6 无左右子树,因此节点 6 遍历完成,回到节点 3 并遍历其右子树,找到节点 7;
节点 7 无左右子树,因此以节点 3 为根节点的子树遍历完成,同时回归节点 1。由于节点 1 的左右子树全部遍历完成,因此整个二叉树遍历完成;
大学学过数据结构这门课的童鞋,看到这些应该会回忆起很多内容了,中序遍历(左根右)和后序遍历(左右根)思路也是类似的,就不展开了。
下面给出递归和非递归2种前序遍历的代码实现:
/**
* 前序遍历,递归方式
* @param root
* @return
*/
public static List resultList = new ArrayList<>();
public static List preOrder(TreeNode biTree) {
if (biTree != null) {
resultList.add(biTree.value);
}
TreeNode leftTree = biTree.left;
if(leftTree != null) {
preOrder(leftTree);
}
TreeNode rightTree = biTree.right;
if(rightTree != null) {
preOrder(rightTree);
}
return resultList;
}
看代码可以发现比较简单,只要注意递归时左右子节点的先后顺序即可。
/**
* 前序遍历,非递归方式
* @param biTree
* @return
*/
public static List preOrder1(TreeNode biTree) {
List resultList = new ArrayList<>();
Stack stack = new Stack();
while(biTree != null || !stack.isEmpty()) {
while(biTree != null) {
resultList.add(biTree.value);
stack.push(biTree);//入栈
biTree = biTree.left;
}
if(!stack.isEmpty()) {
biTree = stack.pop();//出栈
biTree = biTree.right;
}
}
return resultList;
}
这段代码要特别说明一下,这里用到了栈Stack来处理二叉树节点的访问顺序,对栈这种数据结果不了解的话又需要补课了。简单的说下吧,栈就像一个开口的桶,放入(入栈)拿出(出栈)都通过最上面的桶口(栈顶),所以最先放进去的东西就排在桶底(栈底)了,简称:先进后出或者后进先出。
那么上面代码第一次外层循环biTree是根节点不为null,满足条件进入第二层循环,resultList成功add到根节点的值,然后将当前的根节点入栈,并且复制当前节点到根节点的左孩子节点(符合前序遍历的:根左右顺序),这样就会在这个循环内将这颗左孩子树的所有节点都遍历完,遍历到叶子节点后没有子节点了,biTree为null,跳出第二层循环,继续执行第一层循环内的下面代码,由于栈内不为空,开始出栈,后进入的先出,并且把biTree赋值给右孩子节点,所以相当于当前层次回到了上一层,依次循环往复,直到遍历结束。
