几幅图，干趴队列-技术圈

今天继续来给大家上一盘硬菜，保证喂个半饱——嗝。和栈一样，队列（queue）也是一个非常有用的数据结构。同时又非常特殊，它只允许在队尾（rear）插入元素，在队首（front）删除元素，也就是一端进，一端出。

在网上购票普及之前，我们大多数人需要到车站的购票大厅买票，经常是排队排到水泄不通，queue 就和现实中的排队是一模一样的，排在队首的先买到票，然后离开，紧跟着的人移动到队首，直到队列消失。

队列遵循的是 First In First Out，缩写为 FIFO，也就是先进先出，第一个进入队列的第一个先出来。

在上面这幅图中，1 比 2 先进入队列，也比 2 先出队列，规规矩矩的。

对于队列这样一个数据结构来说，它有两个常见的动作：

enqueue，我个人喜欢把它译作入队，指的是把元素放入队列这个动作。
dequeue，出队，指的是把元素从队列中移除这个动作。

明白了队列的基本操作后，我们来深入地思考一下，队列是如何工作的。

1）建立顺序的队列结构需要为其静态分配或者动态申请一串连续的存储空间。

2）然后设置两个指针进行管理：一个队首指针 FRONT，指向队首的元素，一个队尾指针 REAR，指向队尾的元素。初始化的时候，FRONT 和 REAR 都设置为 -1。

3）入队时

检查队列是否已经满了，需要一个 isFull() 的方法来判断；
对于第一个元素，设置 FRONT 的值为 0；
每次在队尾插入一个元素时，REAR 加 1，然后把队尾的元素指向 REAR。

4）出队时

检查队列是否为空，需要一个 isEmpty() 的方法来判断；
用一个临时变量来保存队首的元素，以便出队后返回；
每次在队首删除一个元素时，FRONT 加 1；
如果是最后一个元素，重置 FRONT 和 REAR 为 -1。

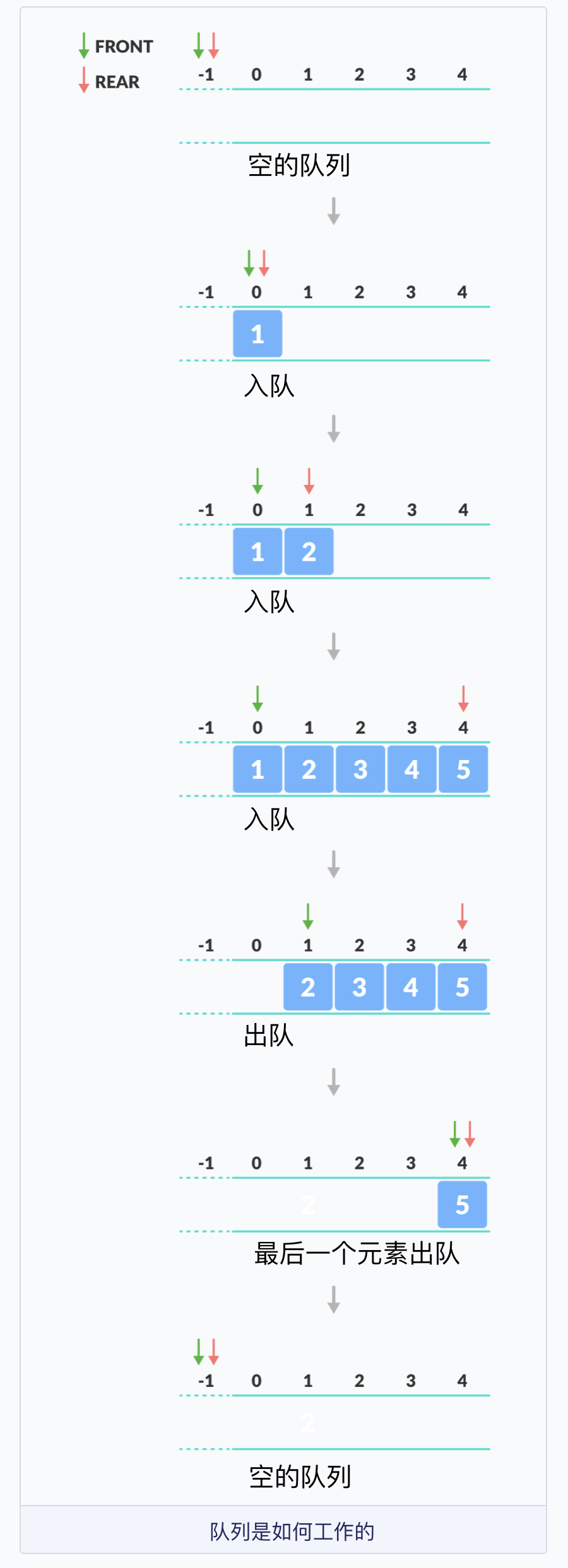
队列为空的时候，FRONT 和 REAR 等于 -1；把元素 1 入队的时候，FRONT 变为 1，REAR 加 1 变为 0，queue[FRONT]=queue[REAR] 为 1；把元素 2 入队的时候，REAR 加 1 变为 1，queue[REAR] 为 2，queue[FRONT] 仍然为 1；接着，元素 3 入队；元素 4 入队；元素 5 入队，REAR 变为 4，queue[REAR] 为 5，queue[FRONT] 仍然为 1。

元素 1 出队的时候，FRONT 为 0，queue[FRONT] 为 1，然后 FRONT 加 1 变为 1；元素 2 出队的时候，queue[FRONT] 为 2，然后 FRONT 加 1 变为 2；接着，元素 3 出队；元素 4 出队；元素 5 出队的时候，queue[FRONT] 为 5，FRONT 为 4，REAR 为 4，出队后，FRONT 和 REAR 重设为 -1。

假设队列中的元素为 int 类型，队列的大小为 5，我们可以用 Java 语言来自定义一个最简单的 queue。它需要 3 个字段：

int queue[]，一个 int 类型的数组，来存放数据
int front，一个 int 类型的队首标记
int rear，一个 int 类型的队尾标记

class Queue {
    int SIZE = 5;
    int items[] = new int[SIZE];
    int front, rear;
}

初始化队列：

Queue() {
    front = -1;
    rear = -1;
}

入队：

void enQueue(int element) {
    if (isFull()) {
        System.out.println("队列已经满了");
    } else {
        if (front == -1)
            front = 0;
        rear++;
        items[rear] = element;
        System.out.println("插入 " + element);
    }
}

出队：

int deQueue() {
    int element;
    if (isEmpty()) {
        System.out.println("队列空了");
        return (-1);
    } else {
        element = items[front];
        if (front >= rear) {
            front = -1;
            rear = -1;
        }
        else {
            front++;
        }
        System.out.println("删除 -> " + element);
        return (element);
    }
}

检查队列是否已经满了：

boolean isFull() {
    if (front == 0 && rear == SIZE - 1) {
        return true;
    }
    return false;
}

检查队列是否为空：

boolean isEmpty() {
    if (front == -1)
        return true;
    else
        return false;
}

来个 main() 方法测试下：

void display() {
    int i;
    if (isEmpty()) {
        System.out.println("队列为空");
    } else {
        System.out.println("\n队首的下标-> " + front);
        System.out.println("元素 -> ");
        for (i = front; i <= rear; i++)
            System.out.print(items[i] + "  ");

        System.out.println("\n队尾的下标-> " + rear);
    }
}

public static void main(String[] args) {
    Queue q = new Queue();

    // 队列为空的时候不允许出队
    q.deQueue();

    // enQueue 5 elements
    q.enQueue(1);
    q.enQueue(2);
    q.enQueue(3);
    q.enQueue(4);
    q.enQueue(5);

    // 队列满了的时候不允许入队
    q.enQueue(6);

    q.display();

    // 出队
    q.deQueue();

    // 打印
    q.display();
}

打印结果如下所示：

队列空了
插入 1
插入 2
插入 3
插入 4
插入 5
队列已经满了

队首的下标-> 0
元素 -> 
1  2  3  4  5  
队尾的下标-> 4
删除 -> 1

队首的下标-> 1
元素 -> 
2  3  4  5  
队尾的下标-> 4

好了，这种基本的队列已经可以正常工作了，但它有一个问题：当已经出队了 N 个元素后，按理说，应该可以再入队 N 个元素，对吧？因为省出来了 N 个空间嘛。

Queue q = new Queue();

// enQueue 5 elements
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
q.enQueue(4);
q.enQueue(5);

// 出队
q.deQueue();
q.deQueue();

q.enQueue(6);
q.enQueue(7);

但事实上，这段代码在运行的时候报错了：

插入 1
插入 2
插入 3
插入 4
插入 5
删除 -> 1
删除 -> 2
Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: Index 5 out of bounds for length 5
 at com.itwanger.queue.Queue.enQueue(Queue.java:23)
 at com.itwanger.queue.Queue.main(Queue.java:89)

看见 ArrayIndexOutOfBoundsException 我们就知道，数组越界了。这是因为我们是用数组实现的队列，在出队的时候 REAR 并没有减小，导致入队的时候 items[rear++] 超出了数组的边界。

可以把问题归咎于我们实现队列的方式上，也可以浅显地认为基本类型的队列存在有局限性。随着入队和出队的连续操作，队列中的元素在不停地变化，队列所占的存储空间也在分配的连续空间中不停的移动。

当 REAR 增加到超出数组大小的范围之后，队列就无法添加新的元素了，事实上还有很多空间可以利用，但它们仍然被已出队的元素占用着——正所谓“附身”啊。除非所有的元素均被移除后， FRONT 和 REAR 被重置，队列才能重新使用。

由于基本类型的队列存在这种局限性，我们就迫切的需要一种新型队列的出现——环形队列（Circular queue）就闪亮登场了。

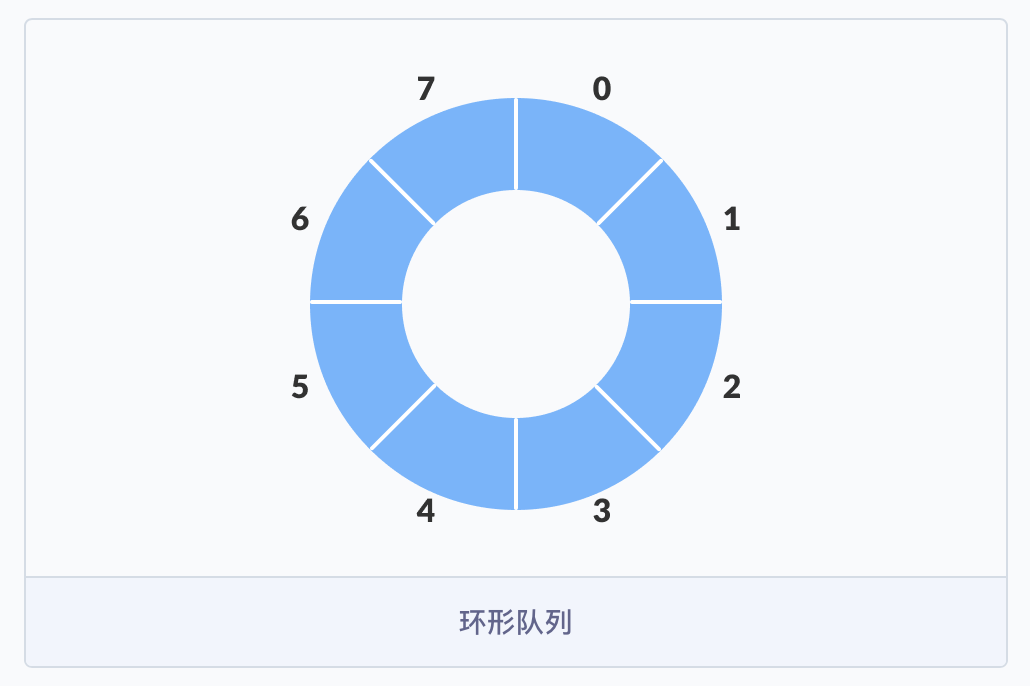
那环形队列是如何工作的呢？它是怎么解决这个问题的呢？

1）同样需要一串连续的存储空间。

2）初始化的时候和基本类型的队列完全一样；

3）入队时

检查队列是否已经满了，此时的条件除了 FRONT = 0 && REAR = SIZE + 1，也就是队首有元素，队尾也有元素时，也就是第一次把队列填满时。还需要再增加一个：FRONT = REAR + 1，也就是队尾紧跟在队首后面的时候，循环把队列填满时。代码如下所示。

boolean isFull() {
    if (front == 0 && rear == SIZE - 1) {
        return true;
    }
    
    if (front == rear + 1) {
        return true;
    }
    return false;
}

一旦 REAR 加 1 后超出了所分配的连续空间，就让它指向连续空间的起始位置。也就是说，REAR 需要重新轮循了，从 0 开始，可以用 (REAR + 1) % SIZE 取余的形式来表示。代码如下所示。

void enQueue(int element) {
    if (isFull()) {
        System.out.println("队列已经满了");
    } else {
        if (front == -1)
            front = 0;
        rear = (rear + 1) % SIZE;
        items[rear] = element;
        System.out.println("插入 " + element);
    }
}

4）出队时

同样的，当 FRONT 加 1 超出了所分配的连续空间，就让它指向连续空间的起始位置。也就是说，FRONT 需要重新轮循了，从 0 开始，可以用 (FRONT + 1) % SIZE 来表示。代码如下所示。

int deQueue() {
    int element;
    if (isEmpty()) {
        System.out.println("队列空了");
        return (-1);
    } else {
        element = items[front];
        if (front >= rear) {
            front = -1;
            rear = -1;
        }
        else {
            front = (front + 1) % SIZE;
        }
        System.out.println("删除 -> " + element);
        return (element);
    }
}

main() 方法的测试代码就不再贴了，和基本类型的队列时差别不大。一图胜千言，我们来画一幅图表示下环形队列的工作方式。

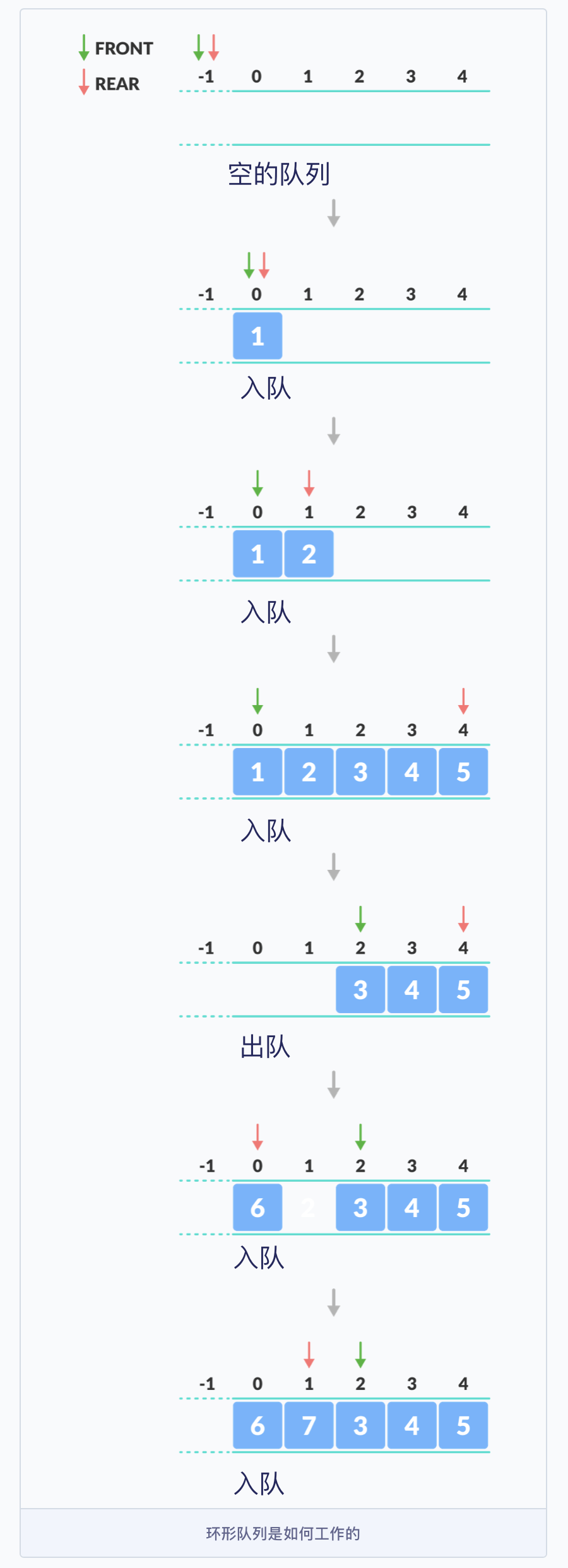
当队列第一次被填满了以后，出队了两个元素，此时下标为 0 和 1 的两个位置空了出来，然后入队元素 6，意味着 6 变成了队尾，也就是 REAR 等于 0 了；再入队元素 7，7 变成了队尾，也就是 REAR 等于 1 了。

现在，来思考一个问题，假如此时执行 deQueue() 方法出队一个元素时，哪一个元素会被移除呢？答案是元素 3，因为此时它在队首，之后是元素 4，元素 5，元素 6，元素 7，虽然直观上看起来不是那么回事，但如果把它想象成一个环形的而不是直线型的就很好理解了。

对比来说，环形队列比普通类型的队列在容量的利用上更充分一点。

除了基本类型和环形队列之外，队列还有优先级队列和双端队列，虽然它们都归到了队列这一类，但其实并不遵循 FIFO 的规则，所以我就打算把它们拎出来单独来讲。

那今天就到这吧，我是沉默王二，希望今天的这盘硬菜能给你喂个半饱，我们下期见~