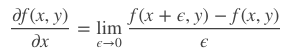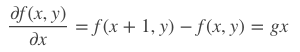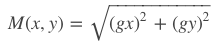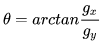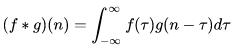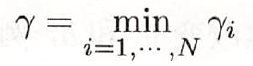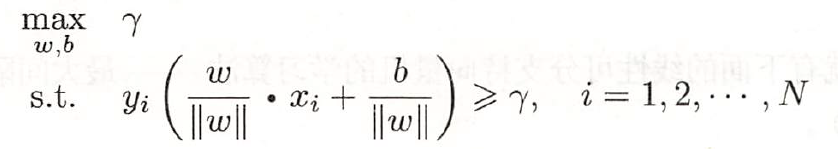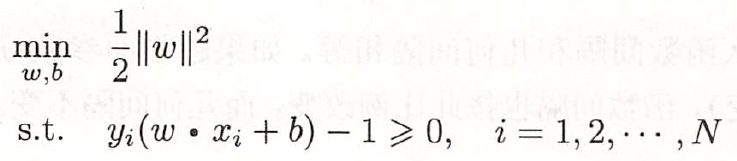图像识别,主要是通过图像的轮廓。所以先提取训练图像的轮廓特征。然后使用SVM支持向量机模型进行学习,从而实现图像识别。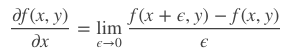
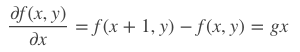
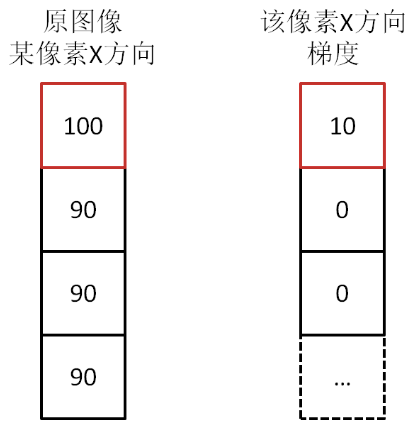
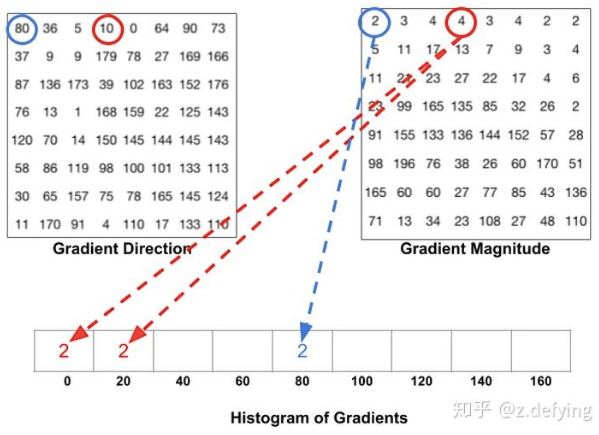
图像的梯度相当于2个相邻像素值(灰度或RGB等其它形式)之间的差值,通过梯度就能了解像素之间的变化强弱,对于变化强的,基本上是图像的轮廓边缘。卷积这个词听着不好理解,大白话理解就是你现在时刻的计算值需要叠加前几次时刻的影响。更形象解释可进入:Sobel等算子(卷积核)进行卷积运算,即通过矩阵运算与像素周边的点一起做相关的处理(平滑、锐化),提取图像的梯度特征。首先把图片划分成多个8*8的cell,每个cell包含8*8*2=128个值(梯度和角度),把这128个值用长度为9的数组来表示,这个数组就是梯度直方图。这种表示方法不仅使得特征更加紧凑,而且对单个像素值的变化不敏感,也就是能够抗噪声干扰。直方图数组的9个数值,对应于角度0、20、40、60... 160。也就是9 bins。角度如果是在两个bin之间,则按20度等分,把梯度分为两部分,分别放到两边。比如上面方向图中蓝圈包围的像素,角度为80度,这个像素对应的幅值为2,所以在直方图80度对应的bin加上2。红圈包围的像素,角度为10度,介于0度和20度之间,其幅值为4,那么这个梯度值就被按比例分给0度和20度对应的bin,也就是各加上2。如果某个像素的梯度角度大于160度,也就是在160度到180度之间,那么把这个像素对应的梯度值按比例分给0度和160度对应的bin。
将这 8x8 的cell中所有像素的梯度值加到各自角度对应的bin中,就形成了长度为9的直方图:
通过9个数的梯度直方图来代替原来很大的三维矩阵,减少了计算量。因每像素的值受光亮度影响很大,从而导致同一张图,亮度不同梯度值相差很大。那就通过归一化,去除光照影响。HOG使用L2范数归一化,假设我们有一个向量 [128,64,32],向量的长度为||128+64+32||2=146.64,这叫做向量的L2范数。将这个向量的每个元素除以146.64就得到了归一化向量 [0.87, 0.43, 0.22]。现在有一个新向量,是第一个向量的2倍 [128x2, 64x2, 32x2],也就是 [256, 128, 64],我们将这个向量进行归一化,你可以看到归一化后的结果与第一个向量归一化后的结果相同。所以,对向量进行归一化可以消除整体光照的影响。HOG把2*2个cell(组成1个block)的直方图联合一起做归一化,划分block是为了把周边信息都考虑到,避免划分正好在边缘时,数值的偏差。得到一个block归一化数值后,不断地平移一个cell,得到整个图的梯度特征。即opencv里HOGDescriptor,一个3781维的向量,winSize(64,128),blockSize(16,16),blockStride(8,8),cellSize(8,8)共3780维特征,加上一维偏移。SVM线性判别函数是wx + b = 0,刚才所求的3780维向量其实就是w,而加了一维就是b,通过训练得到的偏移值。
img = cv2.cvtColor(cv2.imread('./794.jpg'), cv2.COLOR_BGR2GRAY)
normalised_blocks, hog_image = hog(img, orientations=9, pixels_per_cell=(8, 8), cells_per_block=(8, 8), block_norm='L2-Hys',visualize=True)
plt.imshow(hog_image, cmap=plt.cm.gray)
plt.show()
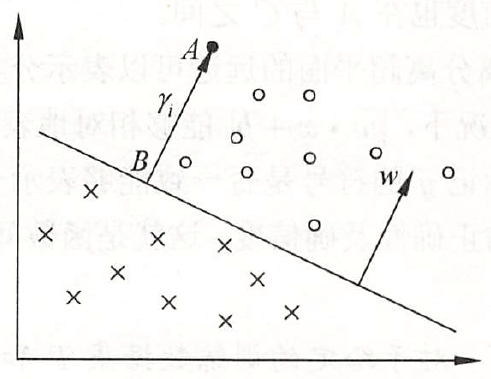
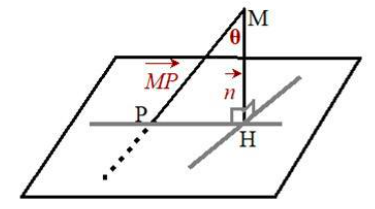
得到了训练的特征数据,下面通过SVM方法实现行人检测:SVM支持向量机找到一个超平面把所有正负类的点分离(正负例在超平面两侧)。如果无法线性分开,则可以使用软间隔方式,找到允许误分类点最少的、软间隔最大的超平面。如果非线性的分类问题,则可以通过核函数,把欧式空间数据映射升到更高维的希尔伯特空间,再去找线性可分的超平面为了正确分类正负类样本,如果离超平面最近点的距离都最大,则其他所有点都可正确分类,以下简述相关概念:样本点(xi, yi)到超平面(w, b)的几何间隔为:定义超平面关于训练集T的几何间隔为所有样本点的最小几何间隔。几何间隔样本点到超平面的带符合的距离,当样本点被正确分类时,等于点到超平面的距离。而模型需要做的就是使得γ最大,当最小的γ都最大了,那其他的样本点就分的更清楚了。1)训练集准备:如果要模型准确性高,训练集得尽量多。IT民工的苦逼苦力,准备3、5千个正、负样本图片,还需要手动标注、裁剪出图像。svm = cv2.ml.SVM_create()
svm.setType(cv2.ml.SVM_C_SVC)
svm.setGamma(0.001)
svm.setC(30)
svm.setKernel(cv2.ml.SVM_RBF)
svm.train(np.array(gradient_list), cv2.ml.ROW_SAMPLE, np.array(labels))
svm.save("svm.xml")
4)利用分类器进行图片检测,以窗口的大小,循环从图像左上角到右下角进行检测,识别图像。for (x, y, roi) in sliding_window(img, 10, (80, 80)):
_, result = svm.predict(np.array([test_gradient]))
相关引用:
https://www.zhihu.com/question/22298352/answer/637156871
https://zhuanlan.zhihu.com/p/85829145
https://blog.csdn.net/krais_wk/article/details/81119237
本文仅做学术分享,如有侵权,请联系删文。