几十张表关联？小Case！-技术圈

作者介绍

qiannzhang（张倩），腾讯云数据库专家工程师，具备多年数据库内核研发经验，在大数据分析领域深耕多年。加入腾讯后，主要负责CDW PG数据库SQL引擎相关特性的研发工作。

背景介绍

CDW PG是腾讯自主研发的新一代分布式数据库，采用无共享的MPP集群架构，具备业界领先的数据分析查询处理能力，适用于PB级海量数据的OLAP应用场景。

在OLAP场景中，多表连接查询是最主要的查询类型之一。CDW PG支持多种连接类型，包括left join、right join、inner join和full join等。对于left join和right join来说，表的连接顺序是固定的，所以可选择的路径相对较少。但对于inner join来说，表的连接顺序可以互换，不同的连接顺序可能产生巨大的性能差异。

那么，当连接查询中表的数量不断增加的时候，CDW PG的优化器是如何找到一个最优的连接顺序路径，从而生成一个高效的查询计划呢?

搜寻最优解

在数据库中，表的扫描路径有顺序扫描、索引扫描和位图扫描等几种扫描方法。如果表上建有多个索引，还可能产生多个不同的索引扫描。优化器面临的第一个问题是，如何在所有的可能中选择一个比较好的扫描路径。

对于涉及单表的查询，通常情况下我们只需要选择代价较小的那一个扫描路径即可。但在多表连接的情况下，除了确定每个表的扫描路径，还需要确定使用的连接算法和连接顺序。CDW PG中支持三种表连接算法，分别是Hashjoin、Mergejoin和Nestloop。

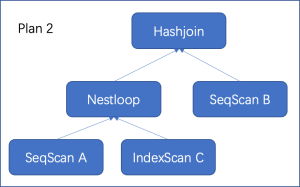
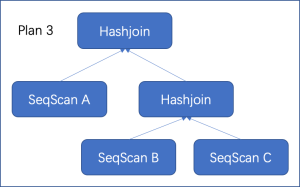
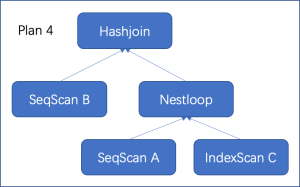
通常情况下，表的扫描路径、连接算法和连接顺序三者之间还存在互相影响。以三表连接A join B join C on a1=b1 and b1=c1为例，假设表C在列c1上建有索引，那么我们可能会得到下面几种计划（实际中远不止下述几种可能）：

显然，这是一个搜索所有路径寻求最优解的过程。在数据库优化器中，路径搜索算法通常有三种：自底向上、自顶向下和随机方法。根据连接表数量的不同，CDW PG的优化器中使用了自底向上的动态规划和随机的遗传算法两种方法。

动态规划搜寻全局最优解

在动态规划算法中，首先需要通过重复使用子问题的解，减少计算量、降低问题复杂度；还有就是能够通过子问题的最优解构造出最终问题的最优解，即问题的解需要具有最优子结构性质。

具体到当前的表连接问题上，优化器采用自底向上的方法，首先从单表开始，每个表支持的每一种扫描路径作为第一层子问题的解。然后，从每两表连接开始考虑，计算出每两表连接的代价，作为第二层子问题的解。

第一层子问题和第二层子问题如下图所示，当前仅简化展示支持单种扫描路径和单种join类型的情况：

两表的连接结果可以认为是一个新表，此时利用第一层和第二层子问题的解，继续进行连接，得到第三层子问题的解，如下图所示：

在实际的查询计划生成过程中，并不是所有的表之间都可以做连接，所以动态规划算法的路径搜索复杂度是基本可控的。例如三表连接A join B join C on a1=b1 and a2=c1，其中表B和表C之间没有连接关系，在第二层子问题中将只有AB、BA、AC、和CA四种可能的连接路径。

但是，如果表的数量过多，动态规划算法仍然存在搜索空间过大的问题，此时CDW PG优化器会采用遗传算法，获得一个局部最优解，从而达到一个性价比较优的结果。

遗传算法搜寻局部最优解

一般来说，遗传算法的实现包括以下几个步骤：

初始化种群：对基因编码，并通过随机的排列组合，生成多个染色体，构成一个新的种群，并计算适应度；
选择染色体：通过随机算法，选择出用于交叉和变异的染色体；

交叉和变异：对染色体进行交叉和变异操作，产生新的染色体加入到种群；
淘汰染色体：对新染色体进行适应度计算，淘汰种群中不良的染色体。

具体到当前的表连接问题上，优化器将参与连接的表作为基因、不同的连接路径作为染色体、连接路径的总代价作为适应度。在每次迭代中，通过对随机选取的染色体进行交叉操作，产生新的连接路径，并通过适应度计算，淘汰不良的染色体，经过N轮之后获取一个局部最优的连接路径。

在CDW PG中，用户可以通过设置GUC参数enable_geqo选择是否开启使用遗传算法，并可以通过设置GUC参数geqo_threshold，选择在连接表的数量大于等于该阈值时使用遗传算法。

例如，当设置enable_geqo=true并且geqo_threshold=12时，表示当连接表的数量不小于12时，优化器将使用遗传算法生成连接路径，否则将使用动态规划算法生成连接路径。

连接中的数据重分布

CDW PG采用的是MPP架构，其中的数据表支持两种类型的数据分布，Shard分布和Replication分布。Shard分布是指表中的数据按某一列或某几列的值，经过函数计算后选择不同的存储节点，其特点是分布键值相同的数据必然存储在同一个节点上，所有节点存储的数据总和为一份全量的表数据；Replication分布是指表在所有存储节点上都存储着一份全量的表数据。

在CDW PG中，不同分布类型的表在连接选择时，除了扫描路径、连接类型和连接顺序外，还需要根据分布键和连接键的匹配情况，选择对应的数据重分布路径，以保证连接结果正确性。

表Replication分布

当连接两侧的表中，有一侧表是Replication分布时，不管另一侧表的分布键和连接键是否匹配，当前不需要进行数据重分布就可以进行连接操作。

例如A join B on a1=b1，假设A表按a2列Shard分布，B表是Replication分布，此时允许直接进行连接操作，其连接结果是按A表的a2列Shard分布，可继续参与后续的连接路径计算。

连接条件匹配表Shard分布

当连接两侧的表均为Shard分布，并且分布键和连接键是匹配的情况下，由于Shard分布可以保证对应列值相同的数据存储在同一节点上，当前仍然不需要进行数据重分布操作，可直接进行连接。

例如A join B on a1=b1，假设A表按a1列Shard分布，B表按b1列Shard分布，此时允许直接进行连接操作，其连接结果是按A表a1列（等价于B表b1列）Shard分布，可继续参与后续的连接路径计算。

连接条件不匹配表Shard分布

当连接两侧的表均为Shard分布，但是分布键和连接键不匹配的情况下，需要视情况对其中一侧或两侧的表进行数据重分布，将连接键值相同的数据重分布到同一节点上，以保证连接结果的正确性。

例如A join B on a1=b1，假设A表按a2列Shard分布，B表按b1列Shard分布，此时需要将A表按a1列进行数据重分布后，再与B表连接，其连接结果按A表a1列（等价于B表b1列）Shard分布，如下图所示。

同样的查询，假设A表按a2列Shard分布，B表按b2列Shard分布，则需要将A表按a1列、B表按b1列分别进行数据重分布后，再执行连接操作，其连接结果分布方式同上，如下图所示。

在分布键和连接键不匹配的情况下，我们还可以选择将其中一侧的表进行Replication分布后，再执行连接操作，此时连接结果可能具有不同的分布方式。

例如，对上述Plan 2，还可以对表A进行Replication分布，再执行连接操作，其连接结果按B表b2列Shard分布；或者对表B进行Replication分布，再执行连接操作，其连接结果按A表a2列Shard分布，两种计划分别如下图所示。

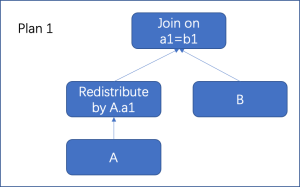
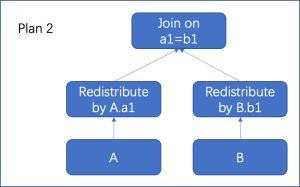
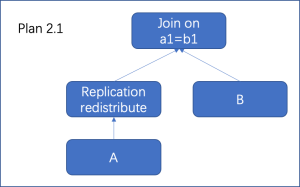
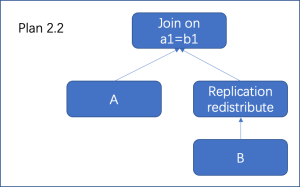
优化器具体选择哪种数据重分布路径，同样是在上述搜寻最优解的算法框架内，按照代价进行选择，此时连接结果的分布方式也有一定影响。

数据分布选择的一些建议

显然，在MPP架构中，数据表分布方式的不同，将直接影响连接查询的性能。通常情况下，我们建议将类似维度表的数据表建成Replication分布，事实表按常用的连接键进行Shard分布，能够不同程度地提升连接查询性能。

点击下方空白 ▼ 查看明日开发者黄历