Language Model Reasoning
自从那篇著名的《Chain of Thought Prompting Elicits Reasoning in Large Language Models》发布以来,一下子引爆了使用 Large Language Models (LLMs) 做推理任务的热潮。同时,越来越多的研究者开始深挖 LLMs 的各种能力。其中,推理能力作为一种可能的“象征着真正的智慧”的能力,在过去的一年里兴许不是被探索和研究得最多的,但肯定是被讨论得最为热烈的,ChatGPT的发布更是将气氛推到了顶峰,LLMs 自此彻底破圈。尽管如此,大家很快就发现,虽然LLMs 的续写或回答能力很强,说起话来语言流畅优美,态度彬彬有礼,但在事实性问题,以及需要深思熟虑,多步推理 (Multi-step Reasoning) 的问题上,LLMs 的表现依然不尽如人意。为了更好地了解 LLMs 与 Reasoning 这个领域的情况与进展,我会在本文中介绍过去一年多的时间里,尝试使用语言模型来解决推理任务的几篇论文。由于能力所限,我无法覆盖所有的相关论文,但会在文末列出更多的相关文献供读者朋友参考。
首先,我将介绍一些背景,因为有些读者可能不熟悉这个领域,然后是现有的工作,最后对它们的共同点和区别做一些总结。
背景介绍
那么,前面总是提到推理 (Reasoning) 这个词,什么是推理?我尝试用自己的语言来解释“推理”的含义,最后发现我写得还不如 ChatGPT,于是这里我就简单地摘抄几句它写的解释:
Reasoning is the process of thinking about something in a logical way in order to form a conclusion or judgment.
Reasoning involves the use of evidence, logic, and critical thinking skills to carefully evaluate and understand information, ideas, and arguments.
Reasoning is a method that allows us to make decisions and draw conclusions based on available information.
翻译过来就是推理是以合乎逻辑的方式思考问题,以形成结论或判断的过程。推理涉及使用证据、逻辑和批判性思维技能来仔细评估和理解信息、想法和论点。推理是一种方法,使我们能够根据现有的信息做出决定并得出结论。凭我高中语文和英语作文经常不及格的水平来看我认为它解释得非常到位了。

目前,较为常见的 NLP 推理任务大概可以被分成上图这三种:数学推理,常识推理以及符号推理。前两种很容易理解,就是字面意思,而最后一种,即符号推理,通常指的是给定一些特定符号代表的状态,然后对它们做一些操作,问题就是最后的状态是什么样的,例如给定一个列表,对其进行旋转操作,问你最终的状态是什么。下图中列出了这三种类型的任务的一些代表性数据集。

下图是上面提到的数据集的一些示例。数学推理任务为绿色,常识推理为橙色,蓝色为符号推理。这张图是借用自 Chain of Thought,后面会介绍。

看到这里不太熟悉语言模型的读者也许还有一些疑问,为什么我们要用语言模型来解决推理任务?为什么不能给每个任务都设计一些专门的模型?比如上面的math word problems,我们可以设计一个复杂的pipeline来抽取这其中的变量和计算关系,最后输出答案,以及什么date understanding,last letter concatenation,coin flip,这些甚至可以通过精心设计的规则达到100%的准确率。
首先,语言模型很灵活,我们不再需要设计一个管道来处理输入的信息。在传统的Knowledge based Question Answering中,涉及到实体抽取、识别关系、检索知识库等等,这是一个非常复杂的过程。而使用语言模型,目前,我们只需要设计一个输入输出的模板,然后它就可以通过 In-context learning 来回答新的问题。最近大火的 ChatGPT 基于的是 *Reinforcement Learning from Human Feedback (RLHF)*,我们甚至不再需要设计模板,只需要直接问问题就够了。
其次,由于超大参数量+超大规模语料的预训练过程,语言模型通常包含了不同领域的丰富知识,这意味着我们不再需要刻意地维护一个结构化的知识库以供检索模型使用。当然,这也有弊端,那就是模型训练结束后,它的知识就固定在了那一刻,往后世界上发生的任何事它都无从知晓了,这也是未来需要解决的一个问题。
最后,语言模型可以用自然语言生成中间推理步骤,相比那些直接输出概率分布的分类模型,这为我们观察模型如何一步步达到最终答案提供了一个窗口。例如一个情感分类问题,语言模型能告诉你某句话里的某个词表达的是不满情绪,因而它将其分为负类,而用类似BERT这样的模型,要么是直接输出一个二分类的概率分布,要么是通过设计模板+完形填空的方式 (This movie is awesome. Sentiment: [MASK]),得到一个看似具有解释性的答案,但是其实模型输出的只不过是从一个二分类概率分布变成了一个全词表的概率分布,经过一些后处理,最终又变成了一个二分类的概率分布。
相关工作
下面正式开始介绍相关的论文。总体上,我把介绍的相关工作分成三个主要的类型,如下图所示:一个生成器加一个验证器,思维链提示 (CoT Prompt) 以及前两种的混合方法。在第一种类型中,生成器负责生成多个推理路径,验证器用于评估这些生成的解答,并选出最终的答案。

思维链提示主要是靠人工编写一些带有详细中间推理步骤的问答范本作为 Prompt 拼在要问的问题前面,模型模仿前面的例子对问题做出详细的推理和解答,这通常被称为语境学习 (In-context learning)。
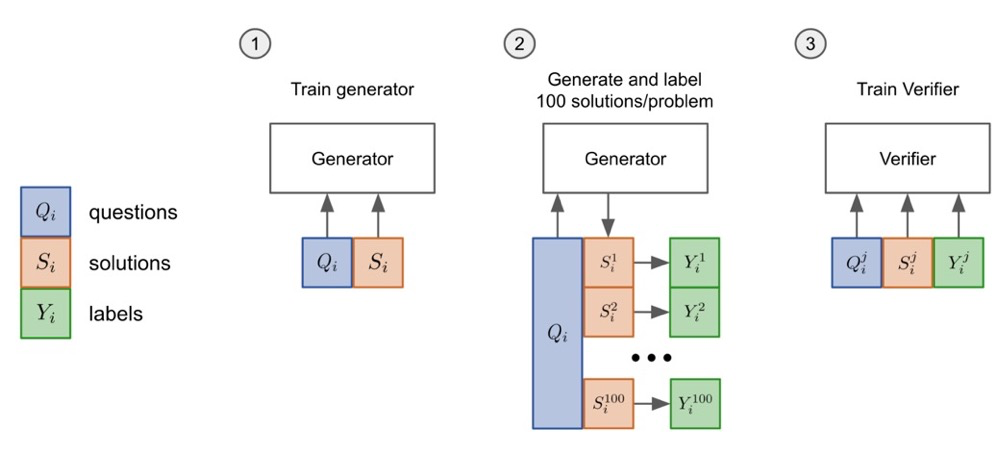
一个 Generator + Verifier 的典型工作是《Training Verifiers to Solve Math Word Problems》,作者来自OpenAI。随这篇论文一起发布的还有当前十分流行的数学题数据集 GSM8K,它包含了大约8000个小学数学问题。因为他们没有给自己的工作起名字,所以后面就简单用OpenAI来指代这项工作。在这项工作中,他们用标准的语言建模目标 (standard language modeling objective) 在GSM8K上训练了一个GPT-3,作为生成器。
然后,他们使用这个生成器为训练集中的每个问题采样100条sulutions。他们使用生成的solutions再额外训练一个GPT-3作为验证器,该验证器对solution中的每个token都预测一个分数,如果最终答案是正确的,预测的分数应该是1,否则应该是0,损失用均方误差计算。

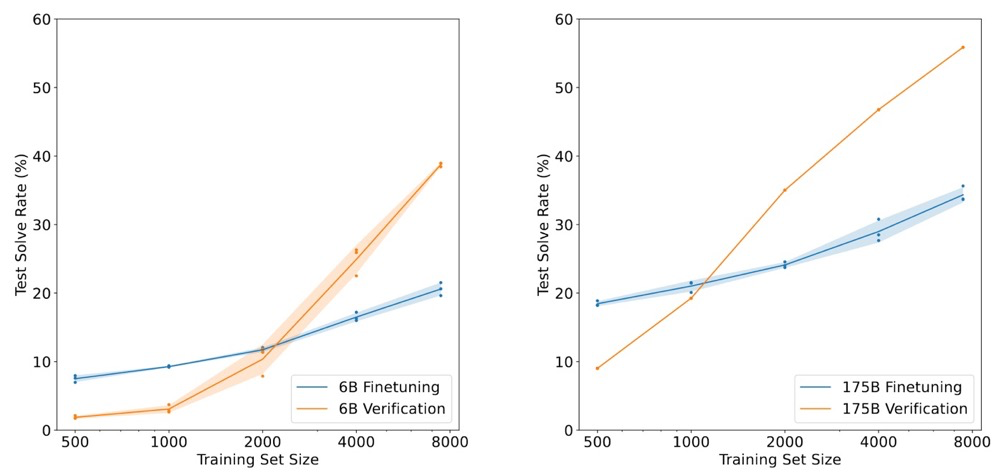
在测试阶段,他们对测试问题采样出100条solutions,然后使用验证器选择得分最高的solution作为最终答案。它将 GPT-3 175B 的准确率从33%的提升到了57%。使用验证器的 GPT-3 6B 达到了约40%的准确率,超过了微调后的 GPT-3 175B。这证明了使用一个额外的验证器来选择solution是十分有效的。值得注意的一点是,他们用 GPT-3 生成推理过程时使用了计算器来辅助 GPT-3,即 GPT-3 只需要列出正确的计算公式,计算器会保证它一定会得到正确的答案。
也许这个做法看起来不那么优雅,为什么不让整个的生成过程都完全由语言模型完成?我个人认为这种做法其实是既好用,又符合常理的。试想一下人在做计算题的时候,能完全不依赖计算器吗?对大多数人来说,两位数的乘除法就已经不是能立马得出答案的了,更不要说三位数及以上的乘除法了,但是人只要能保证计算逻辑的正确性,列出完整正确的公式,那么一切交给计算器就好了,这也是人类能完成各种各样极其庞大复杂的工程的核心所在,那就是人会使用工具。我觉得在这里让语言模型结合计算器来解决数学问题是完全没有问题的,如果反其道而行,非要在语言模型的算术能力上面做文章,死磕语言模型的加减乘除能力,才是本末倒置,毕竟,人发明计算器的目的就是为了把人从各种低阶重复机械的计算中解放出来,人才有更多时间和精力去思考那些更高维度更抽象的东西。

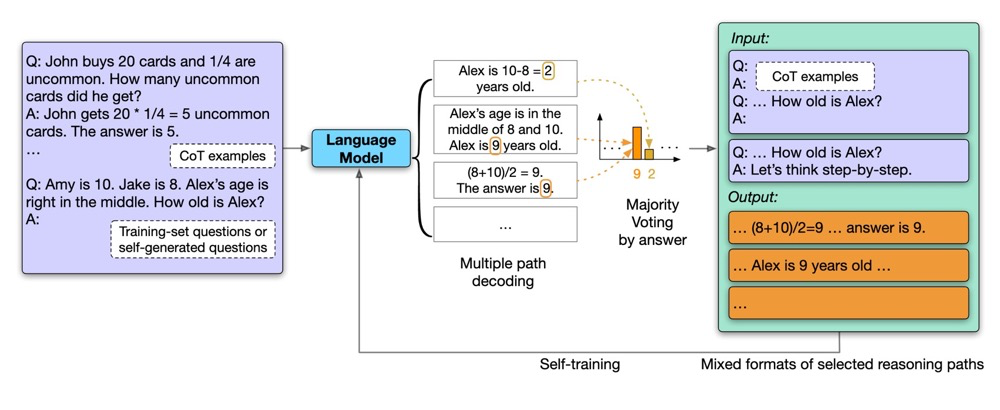
这项工作叫作 Chain of Thought Prompt,它开启了一扇新的大门:提示大规模语言模型去一步一步地解决问题。这个想法非常直接和简单,但其效果却实在令人惊讶。具体方法就是在测试输入的前面拼接了几个由问题、中间推理步骤和最终答案组成的人工写的例子,然后LLMs通过 In-context learning 就学会了要一步一步解决问题,而标准的 few-shot prompt 则效果很差。
在 CoT 论文出来后不久,紧接着 Goolge 又发表了一篇提升 CoT 的论文,就是所谓的自洽 (Self-Consistency)。这个方法非常简单,就是对给定问题采样多个solutions,并通过多数投票获得最终答案。方法其实并不新鲜,采样多个再选取最好的那个之前 OpenAI 早就提出来了,只不过这里更简化了一步,去掉了 Verifier,借助大模型的能力直接用多数投票就能得到不错的效果。其实我觉得OpenAI肯定早在做那篇文章时也试过了用多数投票方法的效果,他们也采样了100条,没有道理不会做一个很简单的多数投票来看看效果如何,毕竟等待训练Verifier完成的时间也没事情做。我个人认为这篇 Self-Consistency 的创新性较为有限,属于是站在了 Chain-of-Thought 肩膀上的一篇手速快的“实验报告”。

虽然性能相当好,但我个人认为自洽性只是一种技巧。同时,和思维链提示一样,它们目前最大的问题是只对非常非常大的语言模型有效。在我的实验中,思维链提示对60亿参数的 GPT-J 几乎不起作用,使用自洽性后在 GSM8K 上只能提高0.5%的准确率。(不过,对大公司来说,对小模型没用可能不算一个问题吧。。。)
自我改进 (Self-Improvement) 是差不多同一班人马的另一项后续工作。在 CoT 与 Self-Consistency 的基础上,它对训练集问题采样出较多的solutions,使用多数投票来获得答案,如果模型对这个答案非常有信心,即相当大比例的solutions都是相同的答案,那么他们就会保留这些solutions,用于之后回头微调语言模型。使用模型生成的solutions来微调它自己,所以这种方法被称为 Self-Improvement。
谷歌对 PaLM 540B 进行了微调,效果当然又提升了,只能说有钱真的可以为所欲为。只是这项工作的可能对普通科研工作者来说没有太多的启发,除非它能证明更小的模型也能自我改进,但是就像前面我所说的,当模型较小的时候,准确率本身已经极低了,根本无法获得像用大模型生成一样的高质量 solutions,那么自我改进又从何谈起呢?
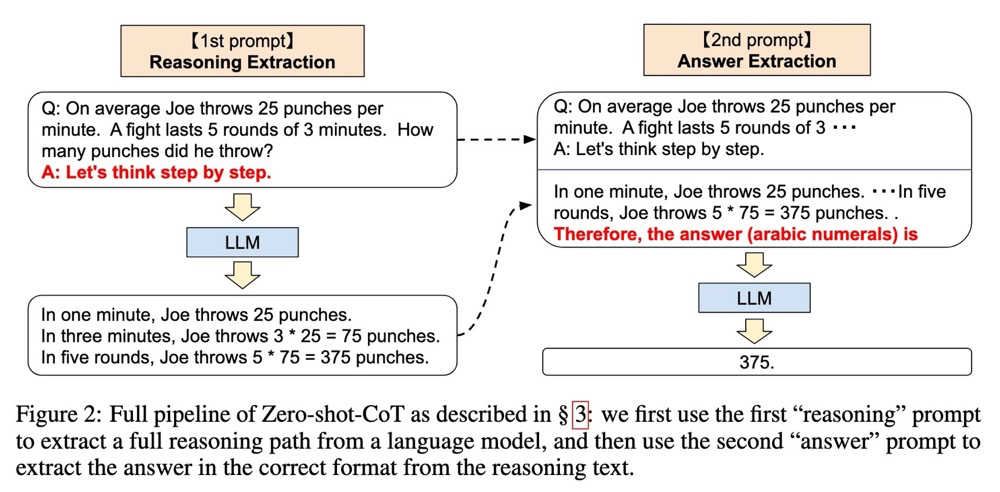
除此以外,还有几项工作专注于改进原始的 CoT。例如这项工作,Zero-shot-CoT,它尝试克服 CoT 需要人工标注的缺点。它使用了两个阶段的提示,首先加入一个提示“让我们一步一步地思考”,就可以使LLMs一步一步地写出推理过程。然后,他们使用一个能够抽取答案的提示来获得最终的答案。其效果非常令人惊讶,在一些数据集上甚至可以和 Few-shot-CoT相媲美,虽然有些数据集还是差了不少,总体上我认为这项工作是非常简洁和优雅的。这项工作也和 CoT 一起中了NeurIPS。
Automatic CoT 是另一项后续工作。尽管 Zero-shot-CoT 很简单,表现也不错,但它比 Few-shot-CoT 还是要差一些的。这项工作尝试使用 Zero-shot-CoT 来构建 Few-shot-CoT 的例子,以此消除 Zero-shot-CoT 和 Few-shot-CoT 之间的差距。
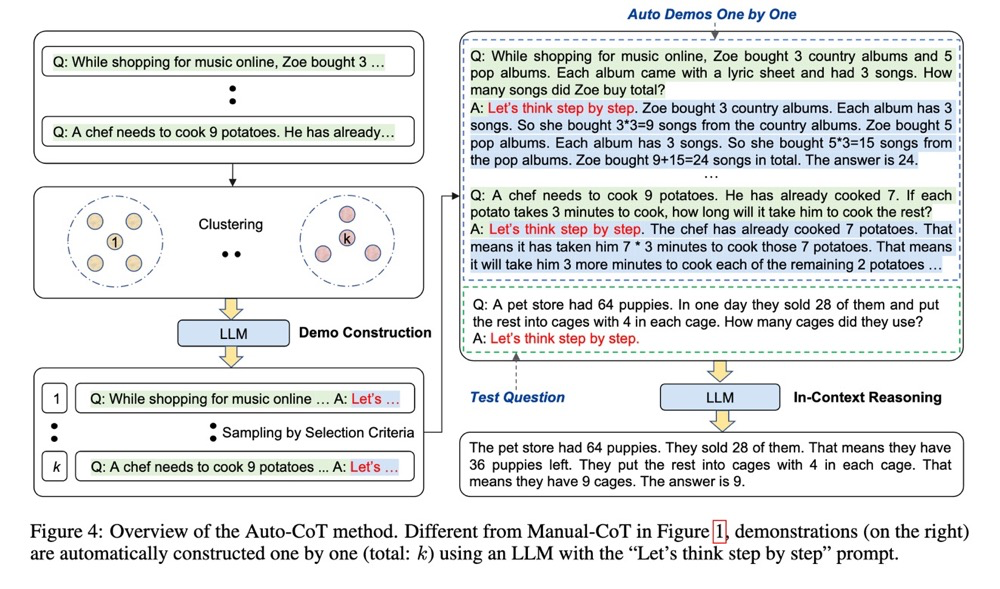
具体来说,该方法是首先用k-means将训练集中的问题分成k个cluster,对于每个cluster,根据问题与聚类中心的距离进行排序,返回排序后的问题列表。接着,遍历这个问题列表,使用 Zero-shot-CoT 编写问题的推理路径,当生成的solution的质量满足要求时,将这个例子保存,作为之后 Few-shot-CoT 的prompt,同时打破当前的循环,在下一个cluster上重复上述过程,构建另一个范例。

最终的效果确实不错,但是可能将其称为 Automatic CoT 还是有些不那么确切,毕竟整个过程并不是那么的 automatic。这篇工作也中了 ICLR 2023。
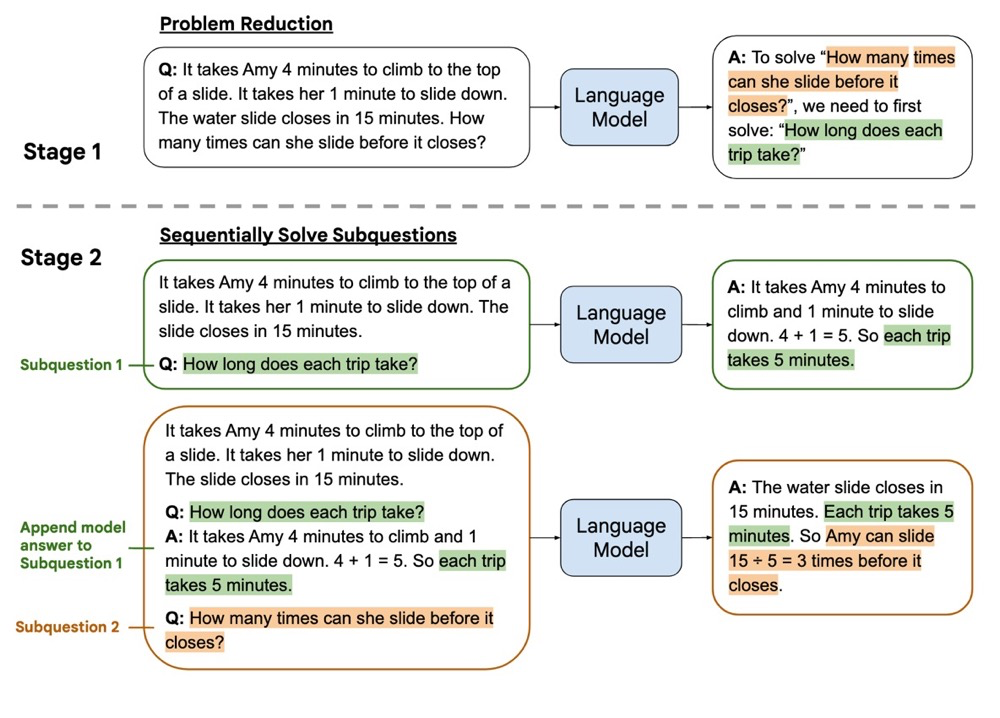
另一项与 CoT 提示非常相似的工作是 least-to-most prompt。其思路是将复杂的问题简化为较容易的子问题,并按顺序解决这些子问题,最终解决原始问题。
DIVERSE 结合了 CoT 和验证器。主要有两个方面的改进,首先它使用了更多样的 few-shot 例子并证明了其有效性,这也被后来的 automatic CoT 工作再一次证明;其次是它训练了一个额外的验证器来为每个推理路径产生一个分数。与OpenAI和Google的工作不同的是,OpenAI使用一个验证器来选择最高分的solution,而Google则使用多数投票来选择最终答案,DIVERSE 使用验证器预测的分数作为权重来投票选择最终答案。
11月有三篇idea比较类似的文章挂在arxiv上,分别是《Teaching Algorithmic Reasoning via In-context Learning》,《PAL: Program-aided Language Models》和《Program of Thoughts Prompting: Disentangling Computation from Reasoning for Numerical Reasoning Tasks》。它们背后的想法比较相似,尽管实施细节有些不同。PAL 这篇文章使用 prompt 来提示 LLMs 写 python 代码,而把最终的计算留给 python 解释器。事实上,应用额外的工具来处理计算应该算是由 OpenAI 在他们最早的工作中提出的,他们提出利用计算器来处理语言模型生成的方程式。我认为他们之间的区别在于它提示 LLMs 写下并保存中间变量,以便最终用编程语言计算结果,而不是通过“=”号来触发调用计算器。

到目前为止,本文所介绍的所有工作都是基于超大语言模型的,难道推理问题只是参数千亿规模的 LLMs 的游戏?下面介绍两篇没有依赖这些超大模型来解决推理任务的工作。
第一篇是《STaR: Self-Taught Reasoner Bootstrapping Reasoning With Reasoning》,这项工作叫作 STaR。具体来说,他们用 few-shot 提示了一个语言模型来生成推理过程的例子,并过滤出答案正确的那些例子,以便进一步微调语言模型。不断重复这个过程,使用改进后的模型来生成下一次的训练集。但这个方法的性能增益很快就饱和了,因为前一个循环中未能解决的问题,到了下一个循环还是没能解决。因此,他们提出了一种叫做 合理化 (rationalization) 的方法,即在问题中加入一个提示,事实上就是直接告诉语言模型哪个答案是正确的,并希望语言模型能写出一个合理的推理过程。

在常识推理任务上,STaR 表现良好,可与微调后的GPT-3相媲美。但是在像GSM8K这样的更难的数据集上,它的表现却远远不能令人满意。正如下图所示,一个只有几十亿个参数的语言模型似乎不可能在困难的推理问题上取得与那些有上千亿参数的模型相当的性能,比如GSM8K。CoT prompt 都不起作用,直接微调 + STaR 也不起作用。

但是,有一项工作证明了这不是真的,像 GPT-J 这样的模型在数学推理任务上可以与那些 LLMs 相媲美,甚至超过它们。《Solving Math Word Problem via Cooperative Reasoning induced Language Models》这篇工作借鉴了认知科学的理念,尤其是双过程理论(dual process theory)。人类的推理有一个双过程框架,由一个即时反应系统(系统1)和一个深思熟虑的推理系统(系统2)组成,整个推理由它们的交互决定。作者设计了一个类似人类的推理架构叫作 CoRe,系统1作为生成器,系统2作为验证器。

整体的方法框架如下图所示。
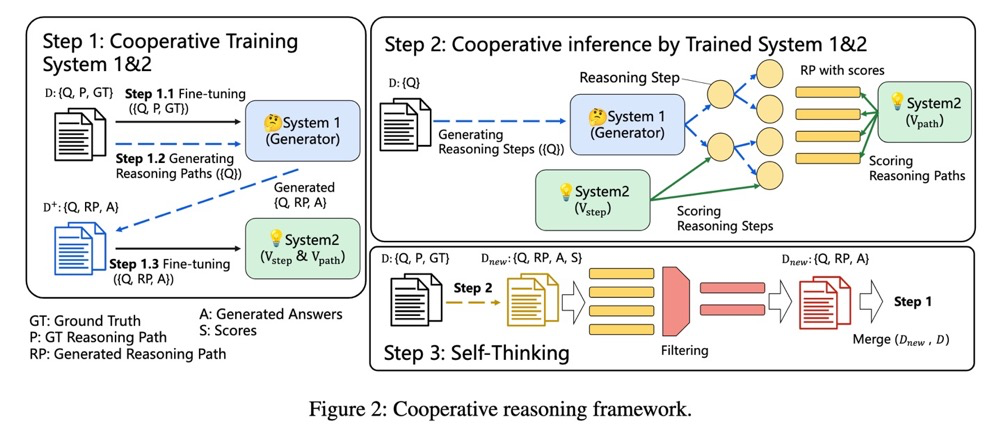
在 Step 1,作者 follow 了 OpenAI 的原始工作。
在 Step 2,不同于之前的工作是在完成所有的生成后再使用验证器来选择 solution,作者认为在生成的过程中间提供反馈是非常重要的,这样的话对推理路径的搜索就是在指导下进行的,那些高质量的路径会被更多地探索。作者使用了了两个验证器,一个是 GPT-J 用于提供 token-level 反馈,另一个用 DeBERTa 用于提供 sentence-level 反馈。这种树状搜索过程与蒙特卡洛树搜索(MCTS)算法非常相似,因此作者利用这种算法将生成器和验证器结合起来,让它们共同解决推理问题。
在 Step 3,为了进一步提高模型的推理能力,作者利用这个闭环的协同推理框架来生成更多的例子以进一步微调语言模型和验证模型。值得注意一点是,作者发现直接用最终答案来过滤生成的例子效果并不理想。相反,他们通过生成器和验证器的合作来过滤它们,所以过滤也是一个协同过程,作者把这个过程称为自我思考(Self-Thinking)。最后重复 Step 2 和 Step 3 直到性能饱和。
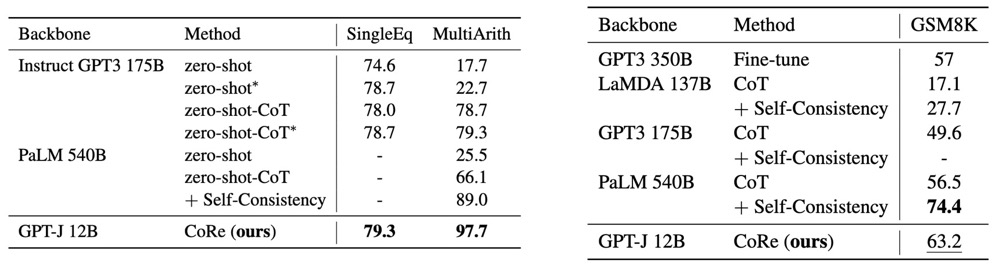
作者在 GSM8K 上对模型进行了微调,而在其他数学推理数据集上进行 zero-shot。可以看出,推理能力可以在同一领域内转移,在GSM8K上的微调有助于语言模型解决其他数学推理问题。使用了 CoRe 的 GPT-J 可以与那些超大的语言模型相媲美。即使在最难的数据集GSM8K上,它也超过了OpenAI 以前的微调 SoTA,后者使用两个 GPT-3 175B,一个作为生成器,一个作为验证器。在其他数据集上的 zero-shot 结果也超过了之前的 fine-tune SoTA。

总结
下图是对这些工作的特点的一个简单总结:

可以预见的是,在未来的一段时间里 LLMs 与 Reasoning 将会吸引更多的研究者参与进来。同时,ChatGPT 的能力还在被不停地探索和挖掘,以往那些简单的下游任务,如情感分类,摘要,文本纠错,风格迁移,在这些超大模型出现之后,极有可能自此退出研究界,只在工业界里的某些特定场景下被继续研究。不管怎么样,新技术产生问题一定还是要比它能够解决的问题要多的,它会解放我们研究那些较为简单低阶任务的精力,从而让我们有更多时间去研究如何解决更加有挑战性的问题,那些曾经想都没想过或者无从下手的问题,现在正等着我们一个个去攻破。
参考文献
[1] Training Verifiers to Solve Math Word Problems
[2] Chain of Thought Prompting Elicits Reasoning in Large Language Models
[3] Self-Consistency Improves Chain of Thought Reasoning in Language Models
[4] Large Language Models Can Self-Improve
[5] Large Language Models are Zero-Shot Reasoners
[6] Automatic Chain of Thought Prompting in Large Language Models
[7] Least-to-Most Prompting Enables Complex Reasoning in Large Language Models
[8] On the Advance of Making Language Models Better Reasoners
[9] Teaching Algorithmic Reasoning via In-context Learning
[10] PAL: Program-aided Language Models
[11] Program of Thoughts Prompting: Disentangling Computation from Reasoning for Numerical Reasoning Tasks
[12] STaR: Self-Taught Reasoner Bootstrapping Reasoning With Reasoning
[13] Solving Math Word Problem via Cooperative Reasoning induced Language Models
