硬肝！超详细matplotlib基础介绍！！！-技术圈

来源：逐梦er
https://zhumenger.blog.csdn.net/article/details/106530281

【导语】：出色的数据可视化，会让你的数据分析等工作锦上添花，让人印(升)象(职)深(加)刻(薪)。matplotlib是python优秀的数据可视化库，python数据分析必备利器，本文专门为你整理了matplotlib详细使用方法，来学习吧！

--- 以下是正文 ---

数据可视化非常重要，因为错误或不充分的数据表示方法可能会毁掉原本很出色的数据分析工作。

matplotlib 库是专门用于开发2D图表（包括3D图表）的，突出优点：

使用起来极为简单。
以渐进、交互式方式实现数据可视化。
表达式和文本使用LaTeX排版。
对图像元素控制力强。
可输出PNG、PDF、SVG和EPS等多种格式。

安装

conda install matplotlib

或者

pip install matplotlib

matplotlib 架构

matplotlib 的主要任务之一，就是提供一套表示和操作图形对象（主要对象）以及它的内部对象的函数和工具。其不仅可以处理图形，还提供事件处理工具，具有为图形添加动画效果的能力。有了这些附加功能，matplotlib 就能生成以键盘按键或鼠标移动触发的事件的交互式图表。

从逻辑上来讲，matplotlib 的整体架构为3层，各层之间单向通信：

Scripting （脚本）层。
Artist （表现）层。
Backend （后端）层。

一、matplotlib的基本用法

import numpy as npimport matplotlib.pyplot as plt
x = np.linspace(-np.pi, np.pi, 30) # 在区间内生成30个等差数y = np.sin(x)print('x = ', x)print('y = ', y)

输出：

x =  [-3.14159265 -2.92493109 -2.70826953 -2.49160797 -2.2749464  -2.05828484 -1.84162328 -1.62496172 -1.40830016 -1.19163859 -0.97497703 -0.75831547 -0.54165391 -0.32499234 -0.10833078  0.10833078  0.32499234  0.54165391  0.75831547  0.97497703  1.19163859  1.40830016  1.62496172  1.84162328  2.05828484  2.2749464   2.49160797  2.70826953  2.92493109  3.14159265]y =  [-1.22464680e-16 -2.14970440e-01 -4.19889102e-01 -6.05174215e-01 -7.62162055e-01 -8.83512044e-01 -9.63549993e-01 -9.98533414e-01 -9.86826523e-01 -9.28976720e-01 -8.27688998e-01 -6.87699459e-01 -5.15553857e-01 -3.19301530e-01 -1.08119018e-01  1.08119018e-01  3.19301530e-01  5.15553857e-01  6.87699459e-01  8.27688998e-01  9.28976720e-01  9.86826523e-01  9.98533414e-01  9.63549993e-01  8.83512044e-01  7.62162055e-01  6.05174215e-01  4.19889102e-01  2.14970440e-01  1.22464680e-16]

画一条曲线

plt.figure() # 创建一个新的窗口plt.plot(x, y) # 画一个x与y相关的曲线plt.show()# 显示图像

画多条曲线以及添加坐标轴和标签

import numpy as npimport matplotlib.pyplot as plt
x = np.linspace(-np.pi, np.pi, 100) # 在区间内生成21个等差数y = np.sin(x)linear_y = 0.2 * x + 0.1
plt.figure(figsize = (8, 6)) # 自定义窗口的大小
plt.plot(x, y)plt.plot(x, linear_y, color = "red", linestyle = '--') # 自定义颜色和表示方式
plt.title('y = sin(x) and y = 0.2x + 0.1') # 定义该曲线的标题plt.xlabel('x') # 定义横轴标签plt.ylabel('y') # 定义纵轴标签
plt.show()

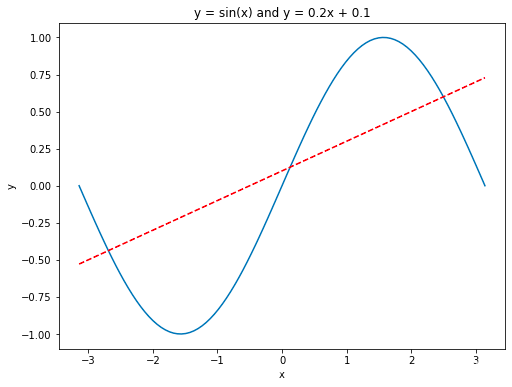
指定坐标范围 and 设置坐标轴刻度

import numpy as npimport matplotlib.pyplot as plt
x = np.linspace(-np.pi, np.pi, 100) # 在区间内生成21个等差数y = np.sin(x)linear_y = 0.2 * x + 0.1
plt.figure(figsize = (8, 6)) # 自定义窗口的大小
plt.plot(x, y)plt.plot(x, linear_y, color = "red", linestyle = '--') # 自定义颜色和表示方式
plt.title('y = sin(x) and y = 0.2x + 0.1') # 定义该曲线的标题plt.xlabel('x') # 定义横轴标签plt.ylabel('y') # 定义纵轴标签plt.xlim(-np.pi, np.pi)plt.ylim(-1, 1)
# 重新设置x轴的刻度# plt.xticks(np.linspace(-np.pi, np.pi, 5))x_value_range = np.linspace(-np.pi, np.pi, 5)x_value_strs = [r'$\pi$', r'$-\frac{\pi}{2}$', r'$0$', r'$\frac{\pi}{2}$', r'$\pi$']plt.xticks(x_value_range, x_value_strs)plt.show() # 显示图像

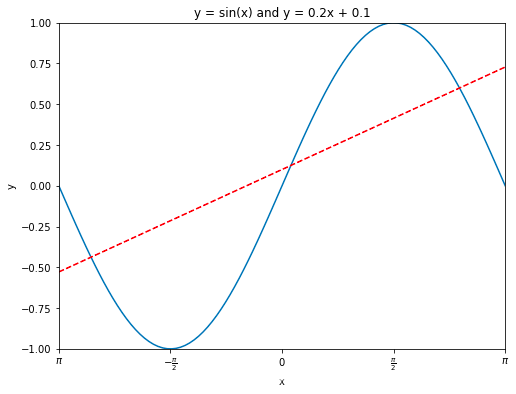
定义原点在中心的坐标轴

import numpy as npimport matplotlib.pyplot as plt
x = np.linspace(-np.pi, np.pi, 100)y = np.sin(x)linear_y = 0.2 * x + 0.1
plt.figure(figsize = (8, 6)) 
plt.plot(x, y)plt.plot(x, linear_y, color = "red", linestyle = '--') 
plt.title('y = sin(x) and y = 0.2x + 0.1')plt.xlabel('x') plt.ylabel('y') plt.xlim(-np.pi, np.pi)plt.ylim(-1, 1)
# plt.xticks(np.linspace(-np.pi, np.pi, 5))x_value_range = np.linspace(-np.pi, np.pi, 5)x_value_strs = [r'$\pi$', r'$-\frac{\pi}{2}$', r'$0$', r'$\frac{\pi}{2}$', r'$\pi$']plt.xticks(x_value_range, x_value_strs)
ax = plt.gca() # 获取坐标轴ax.spines['right'].set_color('none') # 隐藏上方和右方的坐标轴ax.spines['top'].set_color('none')
# 设置左方和下方坐标轴的位置ax.spines['bottom'].set_position(('data', 0)) # 将下方的坐标轴设置到y = 0的位置ax.spines['left'].set_position(('data', 0)) # 将左方的坐标轴设置到 x = 0 的位置
plt.show() # 显示图像

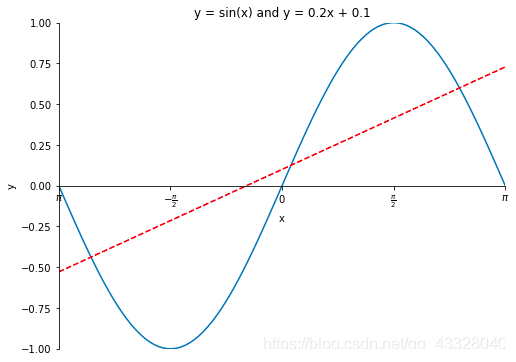
legend图例

使用xticks()和yticks()函数替换轴标签，分别为每个函数传入两列数值。第一个列表存储刻度的位置，第二个列表存储刻度的标签。

import numpy as npimport matplotlib.pyplot as plt
x = np.linspace(-np.pi, np.pi, 100)y = np.sin(x)linear_y = 0.2 * x + 0.1
plt.figure(figsize = (8, 6)) 
# 为曲线加上标签plt.plot(x, y, label = "y = sin(x)")plt.plot(x, linear_y, color = "red", linestyle = '--', label = 'y = 0.2x + 0.1') 
plt.title('y = sin(x) and y = 0.2x + 0.1')plt.xlabel('x') plt.ylabel('y') plt.xlim(-np.pi, np.pi)plt.ylim(-1, 1)
# plt.xticks(np.linspace(-np.pi, np.pi, 5))x_value_range = np.linspace(-np.pi, np.pi, 5)x_value_strs = [r'$\pi$', r'$-\frac{\pi}{2}$', r'$0$', r'$\frac{\pi}{2}$', r'$\pi$']plt.xticks(x_value_range, x_value_strs)
ax = plt.gca() ax.spines['right'].set_color('none')ax.spines['top'].set_color('none')

ax.spines['bottom'].set_position(('data', 0)) ax.spines['left'].set_position(('data', 0)) 
# 将曲线的信息标识出来plt.legend(loc = 'lower right', fontsize = 12)plt.show()

legend方法中的loc 参数可选设置

位置字符串	位置编号	位置表述
‘best’	0	最佳位置
‘upper right’	1	右上角
‘upper left’	2	左上角
‘lower left’	3	左下角
‘lower right’	4	右下角
‘right’	5	右侧
‘center left’	6	左侧垂直居中
‘center right’	7	右侧垂直居中
‘lower center’	8	下方水平居中
‘upper center’	9	上方水平居中
‘center’	10	正中间

二、柱状图

使用的方法：plt.bar

import numpy as npimport matplotlib.pyplot as plt
plt.figure(figsize = (16, 12))x = np.array([1, 2, 3, 4, 5, 6, 7, 8])y = np.array([3, 5, 7, 6, 2, 6, 10, 15])plt.plot(x, y, 'r', lw = 5) # 指定线的颜色和宽度
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])y = np.array([13, 25, 17, 36, 21, 16, 10, 15])plt.bar(x, y, 0.2, alpha = 1, color='b') # 生成柱状图，指明图的宽度，透明度和颜色plt.show()

有的时候柱状图会出现在x轴的俩侧，方便进行比较，代码实现如下：

import numpy as npimport matplotlib.pyplot as plt
plt.figure(figsize = (16, 12))n = 12x = np.arange(n) # 按顺序生成从12以内的数字y1 = (1 - x / float(n)) * np.random.uniform(0.5, 1.0, n)y2 = (1 - x / float(n)) * np.random.uniform(0.5, 1.0, n)
# 设置柱状图的颜色以及边界颜色#+y表示在x轴的上方 -y表示在x轴的下方plt.bar(x, +y1, facecolor = '#9999ff', edgecolor = 'white')plt.bar(x, -y2, facecolor = '#ff9999', edgecolor = 'white')
plt.xlim(-0.5, n) # 设置x轴的范围，plt.xticks(()) # 可以通过设置刻度为空，消除刻度plt.ylim(-1.25, 1.25) # 设置y轴的范围plt.yticks(())
# plt.text()在图像中写入文本，设置位置，设置文本，ha设置水平方向对其方式，va设置垂直方向对齐方式for x1, y in zip(x, y2):    plt.text(x1, -y - 0.05, '%.2f' % y, ha = 'center', va = 'top')for x1, y in zip(x, y1):    plt.text(x1, y + 0.05, '%.2f' % y, ha = 'center', va = 'bottom')plt.show()

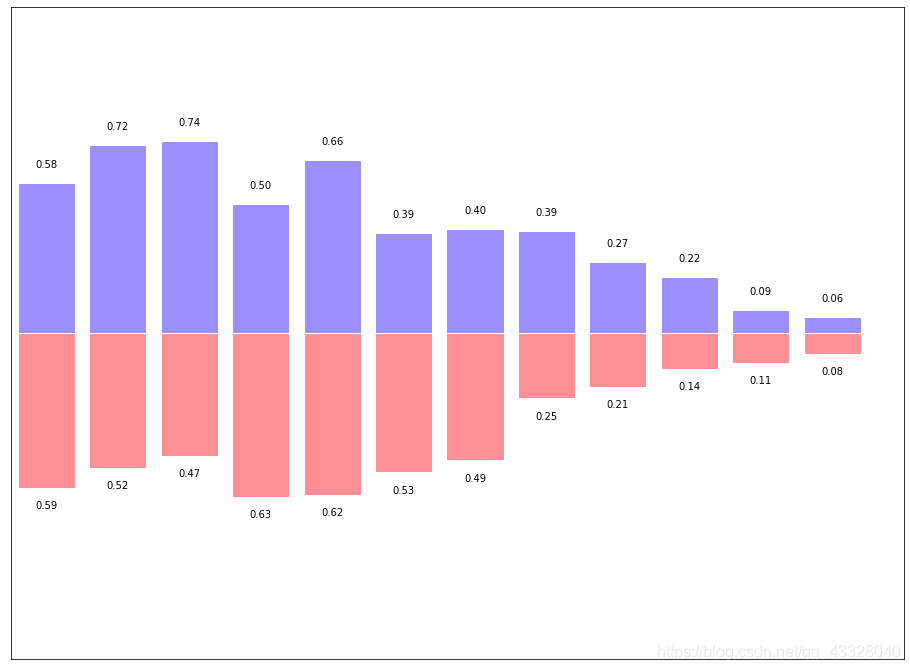
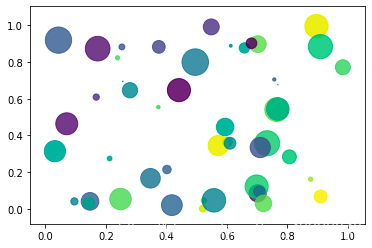
三、散点图

import numpy as npimport matplotlib.pyplot as pltN = 50x = np.random.rand(N)y = np.random.rand(N)colors = np.random.rand(N)area = np.pi * (15 * np.random.rand(N))**2plt.scatter(x, y, s = area,c = colors, alpha = 0.8)
plt.show()

四、等高线图

import matplotlib.pyplot as pltimport numpy as np
def f(x, y):    return (1 - x / 2 + x ** 5 + y ** 3) * np.exp(-x ** 2 - y ** 2)
n = 256x = np.linspace(-3, 3, n)y = np.linspace(-3, 3, n)X, Y = np.meshgrid(x, y)  # 生成网格坐标 将x轴与y轴正方形区域的点全部获取line_num = 10 # 等高线的数量
plt.figure(figsize = (16, 12))
#contour 生成等高线的函数#前俩个参数表示点的坐标，第三个参数表示等成等高线的函数，第四个参数表示生成多少个等高线C = plt.contour(X, Y, f(X, Y), line_num, colors = 'black', linewidths = 0.5) # 设置颜色和线段的宽度plt.clabel(C, inline = True, fontsize = 12) # 得到每条等高线确切的值
# 填充颜色, cmap 表示以什么方式填充，hot表示填充热量的颜色plt.contourf(X, Y, f(X, Y), line_num, alpha = 0.75, cmap = plt.cm.hot)
plt.show()

五、处理图片

import matplotlib.pyplot as pltimport matplotlib.image as mpimg # 导入处理图片的库import matplotlib.cm as cm # 导入处理颜色的库colormap
plt.figure(figsize = (16, 12))img = mpimg.imread('image/fuli.jpg')# 读取图片print(img) # numpy数据print(img.shape) # 
plt.imshow(img, cmap = 'hot')plt.colorbar() # 得到颜色多对应的数值plt.show()

[[[ 11  23  63]  [ 12  24  64]  [  1  13  55]  ...  [  1  12  42]  [  1  12  42]  [  1  12  42]]
 [[ 19  31  71]  [  3  15  55]  [  0  10  52]  ...  [  0  11  39]  [  0  11  39]  [  0  11  39]]
 [[ 22  34  74]  [  3  15  55]  [  7  19  61]  ...  [  0  11  39]  [  0  11  39]  [  0  11  39]]
 ...
 [[ 84 125 217]  [ 80 121 213]  [ 78 118 214]  ...  [ 58  90 191]  [ 54  86 187]  [ 53  85 186]]
 [[ 84 124 220]  [ 79 119 215]  [ 78 117 218]  ...  [ 55  87 188]  [ 55  87 188]  [ 55  87 188]]
 [[ 83 121 220]  [ 80 118 219]  [ 83 120 224]  ...  [ 56  88 189]  [ 58  90 191]  [ 59  91 192]]](728, 516, 3)

利用numpy矩阵得到图片

import matplotlib.pyplot as pltimport matplotlib.cm as cm # 导入处理颜色的库colormapimport numpy as np
size =  8# 得到一个8*8数值在(0, 1)之间的矩阵a = np.linspace(0, 1, size ** 2).reshape(size, size)
plt.figure(figsize = (16, 12))plt.imshow(a)plt.show()

六、3D图

import numpy as npimport matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3D # 导入Axes3D对象
fig = plt.figure(figsize = (16, 12))ax = fig.add_subplot(111, projection = '3d') # 得到3d图像
x = np.arange(-4, 4, 0.25)y = np.arange(-4, 4, 0.25)X, Y = np.meshgrid(x, y) # 生成网格Z = np.sqrt(X ** 2 + Y ** 2)
# 画曲面图              # 行和列对应的跨度         # 设置颜色ax.plot_surface(X, Y, Z, rstride = 1, cstride = 1, cmap = plt.get_cmap('rainbow'))plt.show()

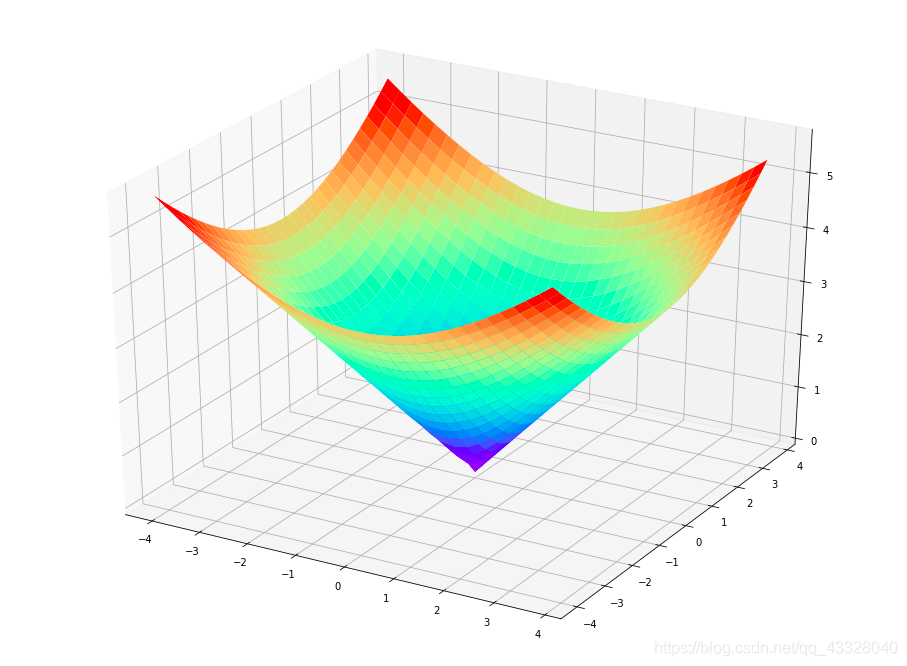
以上是matplotlib基于测试数据的数据可视化，结合实际项目中数据，代码稍加修改，即可有让人印象深刻的效果。

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方“小詹学Python”，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。