今天分享一个开源项目，里面汇总了程序员技术面试时需要了解的 算法和数据结构知识，并且还提供了相应的代码，目前 GitHub 上标星 35000 star，值得一看。

你可以把这个项目的内容当成是一个目录，另外我也稍微补充了一些我之前公众号对应的内容链接，可以配套阅读用来查缺补漏，

在面试前快速浏览一遍对你的面试也是有所帮助的！

GitHub 地址：

https://github.com/kdn251/interviews

栈

• 栈是元素的集合，其包含了两个基本操作：push 操作可以用于将元素压入栈，pop 操作可以将栈顶元素移除。

• 遵循后入先出（LIFO）原则。

• 时间复杂度:

• 索引: O(n)

• 搜索: O(n)

• 插入: O(1)

• 移除: O(1)

链表

• 链表即是由节点组成的线性集合，每个节点可以利用指针指向其他节点。它是一种包含了多个节点的、能够用于表示序列的数据结构。

• 单向链表: 链表中的节点仅指向下一个节点，并且最后一个节点指向空。

• 双向链表: 其中每个节点具有两个指针 p、n，使得 p 指向先前节点并且 n 指向下一个节点，最后一个节点的 n 指针指向 null。

• 循环链表：每个节点指向下一个节点并且最后一个节点指向第一个节点的链表。

• 时间复杂度:

•  索引: O(n)

•  搜索: O(n)

•  插入: O(1)

•  移除: O(1)

队列

• 队列是元素的集合，其包含了两个基本操作：enqueue 操作可以用于将元素插入到队列中，而 dequeue 操作则是将元素从队列中移除。

• 遵循先入先出原则 (FIFO)。

• 时间复杂度:

• 索引: O(n)

• 搜索: O(n)

• 插入: O(1)

• 移除: O(1)

二叉查找树

• 二叉搜索树（BST）是一种特殊的二叉树，其任何节点中的值都会大于或者等于其左子树中存储的值并且小于或者等于其右子树中存储的值。

• 时间复杂度:

•  索引: O(log(n))

•  搜索: O(log(n))

•  插入: O(log(n))

•  删除: O(log(n))

字典树

• 字典树，又称基数树或者前缀树，能够用于存储键为字符串的动态集合或者关联数组的搜索树。树中的节点并没有直接存储关联键值，而是该节点在树中的挂载位置决定了其关联键值。某个节点的所有子节点都拥有相同的前缀，整棵树的根节点则是空字符串。

  
  

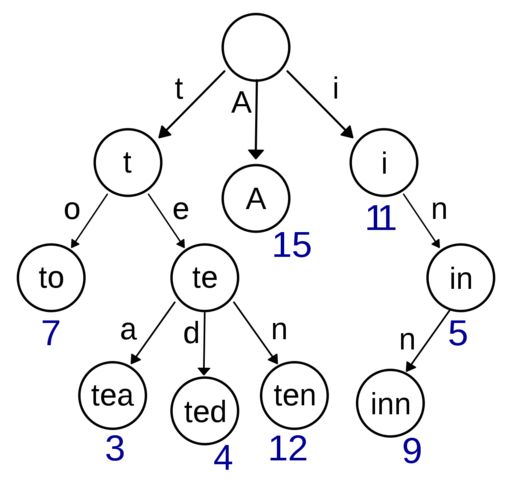
线段树

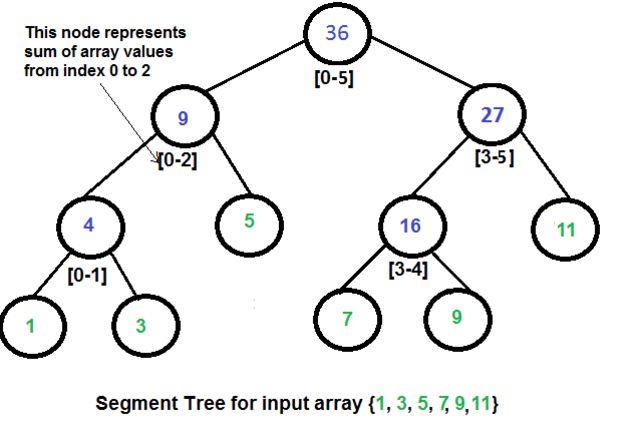
• 线段树是用于存放间隔或者线段的树形数据结构，它允许快速的查找某一个节点在若干条线段中出现的次数.

• 时间复杂度:

• 区间查询: O(log(n))

• 更新: O(log(n))

哈希

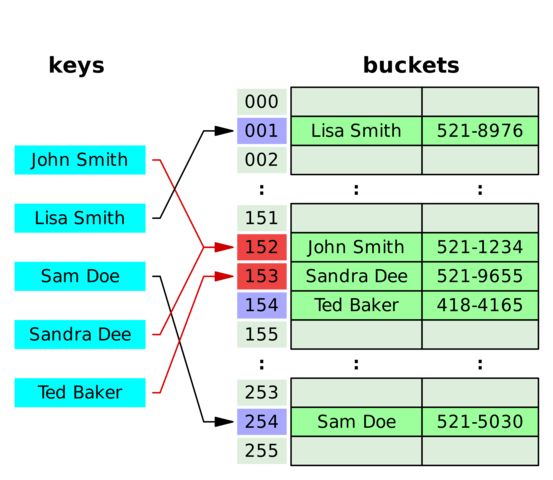
• 哈希能够将任意长度的数据映射到固定长度的数据。哈希函数返回的即是哈希值，如果两个不同的键得到相同的哈希值，即将这种现象称为碰撞。

• Hash Map: Hash Map 是一种能够建立起键与值之间关系的数据结构，Hash Map 能够使用哈希函数将键转化为桶或者槽中的下标，从而优化对于目标值的搜索速度。

• 碰撞解决

• 链地址法（Separate Chaining）: 链地址法中，每个桶是相互独立的，包含了一系列索引的列表。搜索操作的时间复杂度即是搜索桶的时间（固定时间）与遍历列表的时间之和。

• 开地址法（Open Addressing）: 在开地址法中，当插入新值时，会判断该值对应的哈希桶是否存在，如果存在则根据某种算法依次选择下一个可能的位置，直到找到一个尚未被占用的地址。所谓开地址法也是指某个元素的位置并不永远由其哈希值决定。

  
  

图

• 图是一种数据元素间为多对多关系的数据结构，加上一组基本操作构成的抽象数据类型。

• 无向图（Undirected Graph）: 无向图具有对称的邻接矩阵，因此如果存在某条从节点 u 到节点 v 的边，反之从 v 到 u 的边也存在。

• 有向图（Directed Graph）: 有向图的邻接矩阵是非对称的，即如果存在从 u 到 v 的边并不意味着一定存在从 v 到 u 的边。

堆

• 堆是一种特殊的基于树的满足某些特性的数据结构，整个堆中的所有父子节点的键值都会满足相同的排序条件。堆更准确地可以分为最大堆与最小堆，在最大堆中，父节点的键值永远大于或者等于子节点的值，并且整个堆中的最大值存储于根节点；而最小堆中，父节点的键值永远小于或者等于其子节点的键值，并且整个堆中的最小值存储于根节点。

• 时间复杂度:

• 访问最大值 / 最小值: O(1)

• 插入: O(log(n))

• 移除最大值 / 最小值: O(log(n))

排序

归并排序

• 归并排序是典型的分治算法，它不断地将某个数组分为两个部分，分别对左子数组与右子数组进行排序，然后将两个数组合并为新的有序数组。

• 稳定: 是

• 时间复杂度:

• 最优时间: O(nlog(n))

• 最坏时间: O(nlog(n))

• 平均时间: O(nlog(n))

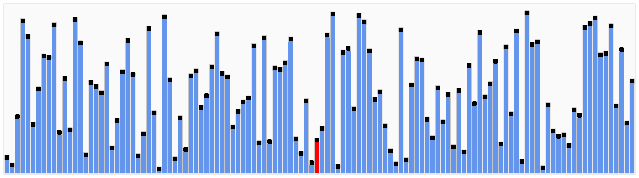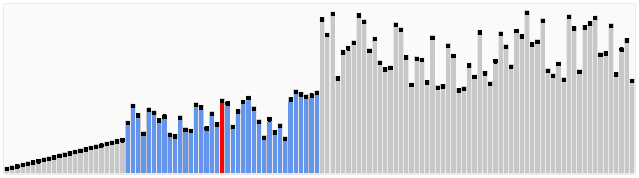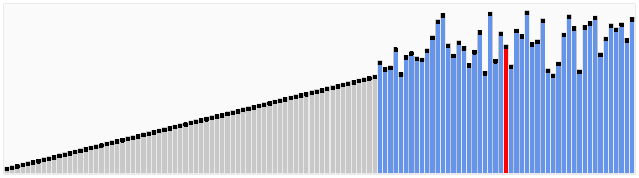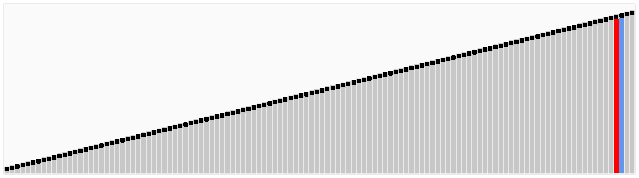
快速排序

• 稳定: 否

• 时间复杂度:

• 最优时间: O(nlog(n))

• 最坏时间: O(n^2)

• 平均时间: O(nlog(n))

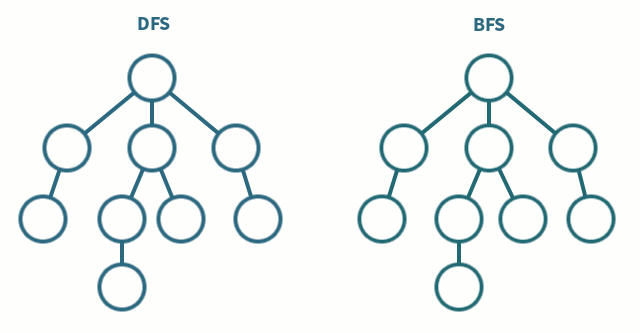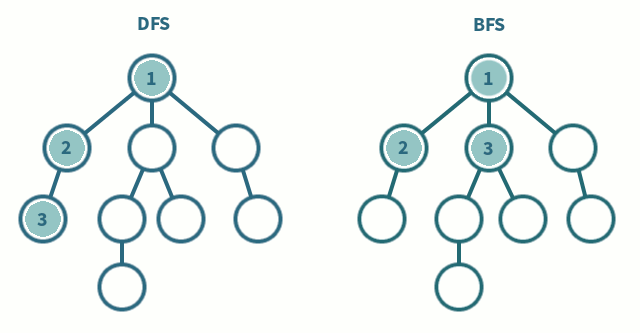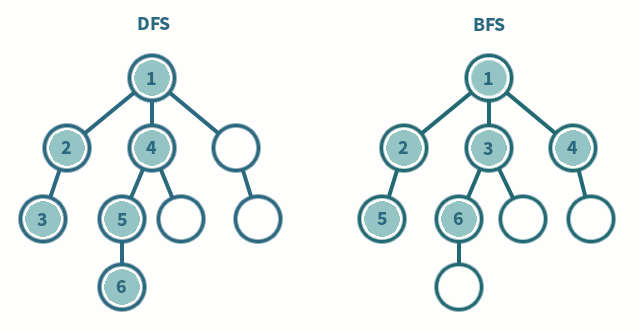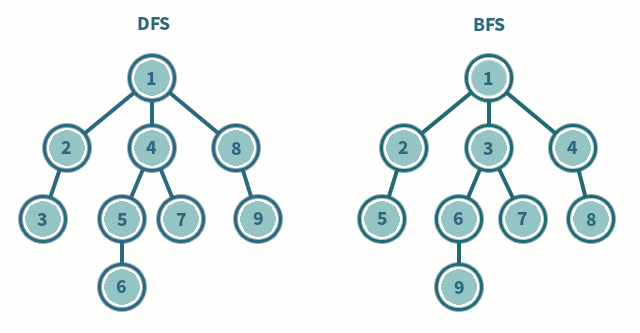
深度优先搜索

• 深度优先算法是一种优先遍历子节点而不是回溯的算法。

• 时间复杂度: O(|V| + |E|)

广度优先搜索

• 广度优先搜索是优先遍历邻居节点而不是子节点的图遍历算法。

• 时间复杂度: O(|V| + |E|)

拓扑排序

• 拓扑排序是对于有向图节点的线性排序，如果存在某条从 u 到 v 的边，则认为 u 的下标先于 v。

• 时间复杂度: O(|V| + |E|)

END