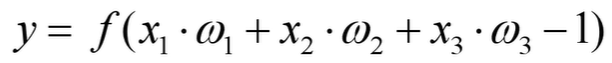一文了解卷积神经网络基础,建议收藏
共
2013字,需浏览
5分钟
·
2020-08-16 13:39
今天给大家讲一下卷积神经网络,主要包括四个部分:卷积神经网络的历史、全连接层、卷积层和池化层。
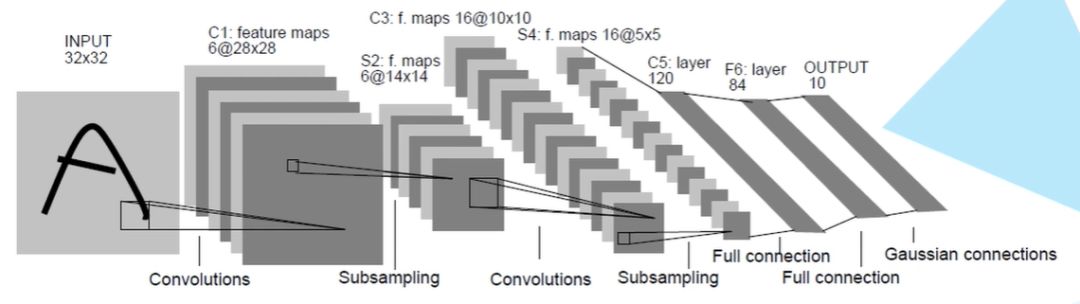
CNN的英文全称是Convolutional Neural Network,雏形是LeCun在1998年发明的LeNet网络结构。那么到底什么是神经网络呢?应该说只要带有卷积层的就可以被叫做卷积神经网络。1986年:Rumelhart和Hinton等人提出了反向传播(Back Propagation)算法。
1998年:LeCun基于BP神经网络训练了LeNet网络,标志着CNN的真正面世。
2006年:Hinton在他们的Science Paper中首次提出了Deep Learning的概念。2012年:其实在2006年Hinton提出深度神经网络之后,受到了很多的质疑,但是在2012年Hinton的学生Alex Krizhevsky在寝室用GPU死磕了一个Deep Learning模型,一举拿下了计算机视觉TOP领域ILSVRC 2012的冠军,在百万量级的ImageNet数据集合上,效果大幅度的超过了传统的方法,准确率从70%提升到80%。
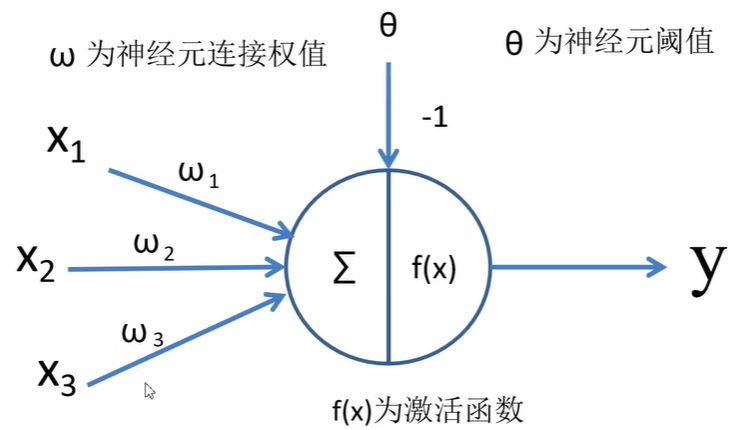
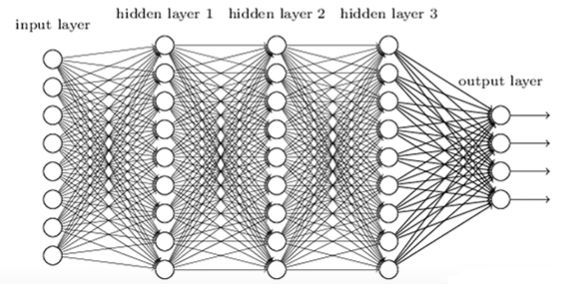
其实全连接层就是模仿大脑的神经元结构,我们可以看到:输出值 = 输入值x经过加权w之后累加的结果再经过激励函数。形式化为:那么我们将神经元按列进行排列,列与列之间进行全连接,就得到了一个BP神经网络。
BP神经网络算法包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行,而调整权值和阈值则从输出到输入的方向进行。
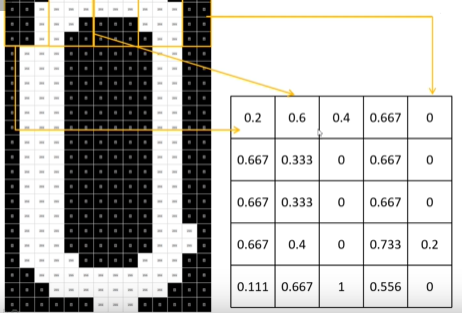
我们拿到一张图片,例如上边第一张图所示拿到的是0,这张图是由若干像素组成,每个像素有RGB三个通道,然后经过灰度化后变成第二张图片,然后将灰度化后的图片进行二值化得到第三张图片。
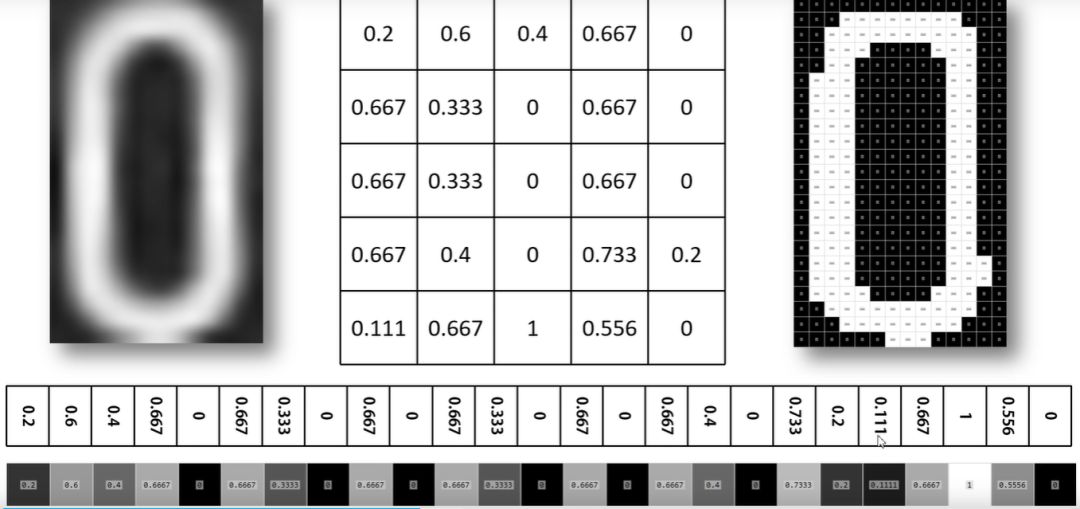
之后我们对图片进行概率处理,例如第一个框中白色块/全部块 = 0.2,经过相应的策略处理之后第一个数值为0.2。以此类推,可以得到上图右边的矩阵。
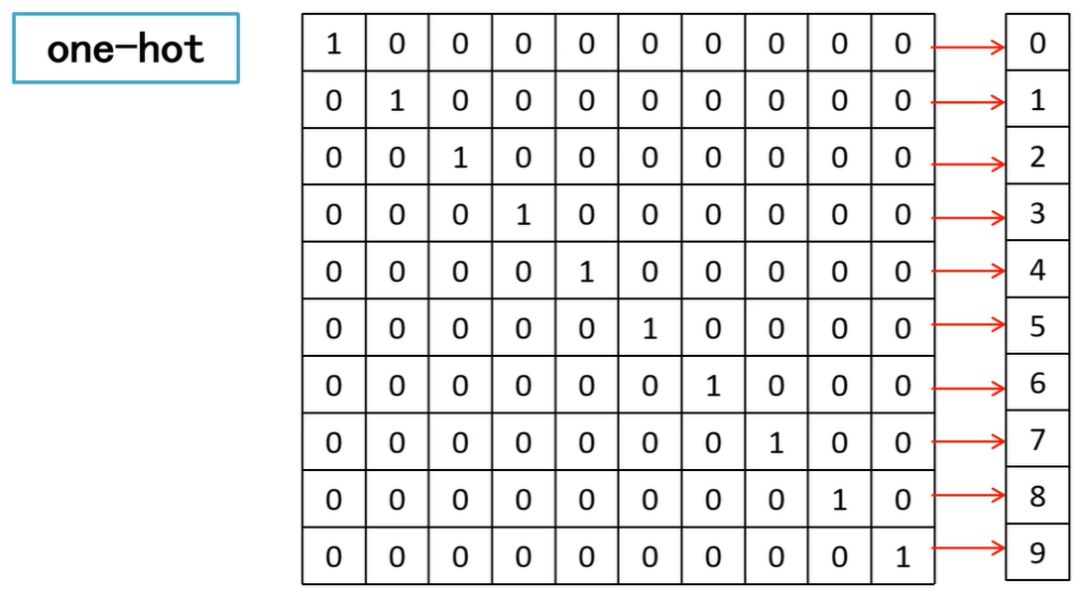
然后我们对这个矩阵进行维度变换和处理,将其变为1*n的行向量,这样处理之后的形式可以使得神经网络更好的输入处理。我们知道神经网络如何输入了,那么最后应该输出什么才可以更好的辨别数字呢?One-Hot编码!
也就是说,每个数字都对应一个编码,如果输入1000000000,则判定为数字0,以此类推。
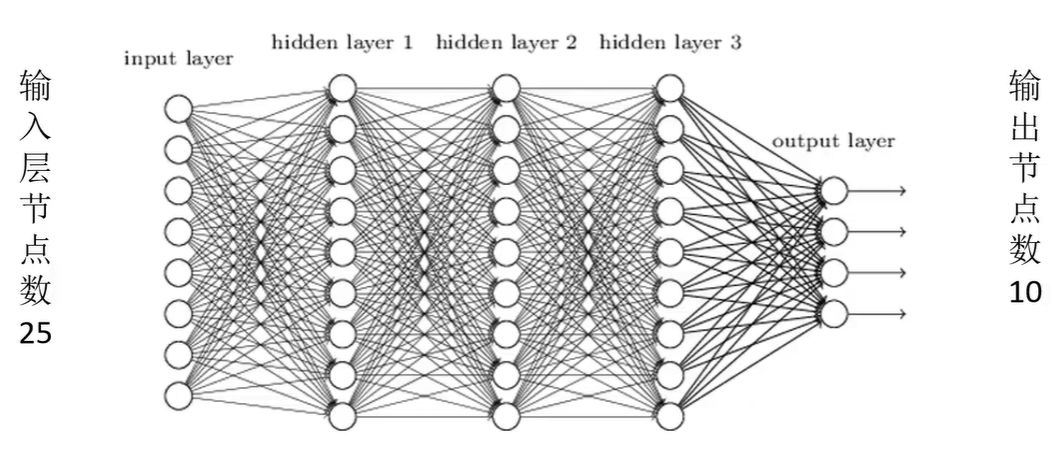
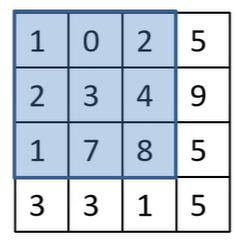
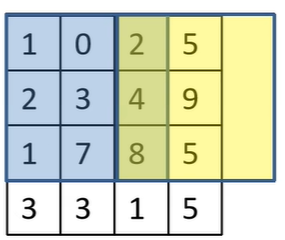
既然有了输入,也有了输出,我们就可以通过神经网络对其进行训练了。首先将输入层的神经元数设置为25个节点,将输出层设置为10个节点,将上边1*n的向量输入到BP神经网络中,然后经过隐藏层最后到输出层onehot编码,输出层通过softmax激活函数可以得到每个数字出现的概率,即可识别数字。到底什么是卷积层?之前的文章中讲过了,有兴趣的可以直接查看。在卷积层的讲解中,想问大家一个问题,卷积核如果越界了应该如何处理?例如下面这样:假设用这么一个矩阵,我们使用3*3的滑动窗口,步长为2,则出现下面这种情况应该如何处理?
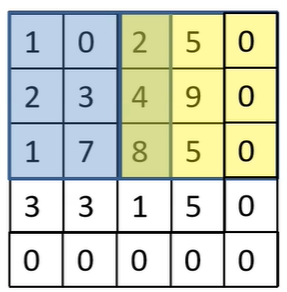
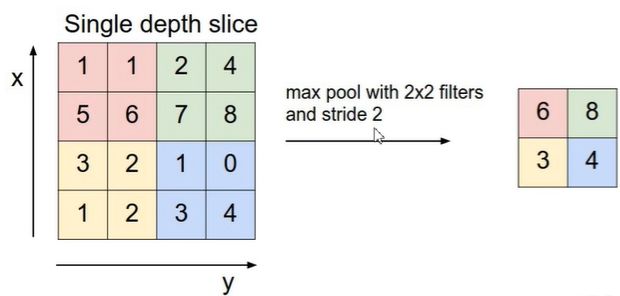
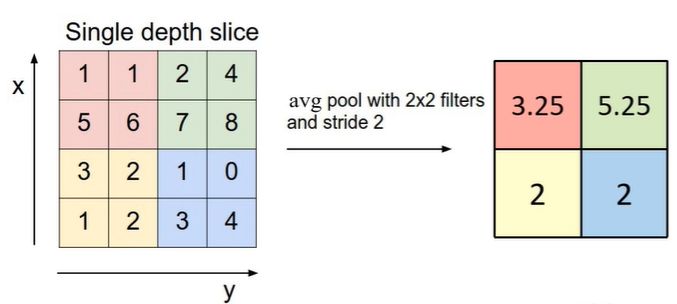
我们可以对其进行使用Padding对其进行补0处理,如下所示:在卷积操作过程中,矩阵经过卷积操作之后大小由下面几个因数决定:经过卷积后的矩阵尺寸大小是有一个规律的,那么给大家一个通用的公式:为什么要存在池化层?因为当前的输入数据太大,有很多冗余信息,那么我们就要想办法对图像矩阵进行下采样,对特征图进行稀疏处理,减少数据运算量。下面通过MaxPooling下采样来给大家看一下到底什么是池化层。上图中红色部分的值为1 1 5 6,我们使用的是MaxPooling,所以取最大值,则右图中红色部分为max(1,1,5,6)=6,以此类推,即可得到下采样结果。类似于最大下采样,同样也有平均下采样层,如下图所示:为了大家更好的理解和使用池化层,我总结了池化层的三个特点:
今天讲的是卷积神经网络的整体架构基础,包括神经网络的发展历史、全连接层、卷积层和池化层,大家有什么见解或者想法都可以在下面留言哦~长按扫码添加Python小助手进入
←_← PY交流群 →_→
▼点击成为社区会员 喜欢就点个在看吧
点赞
评论
收藏
分享

手机扫一扫分享
举报
点赞
评论
收藏
分享

手机扫一扫分享
举报
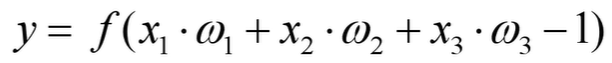


 下载APP
下载APP