无限的路

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 16702    Accepted Submission(s): 9253

Problem Description

甜甜从小就喜欢画图画，最近他买了一支智能画笔，由于刚刚接触，所以甜甜只会用它来画直线，于是他就在平面直角坐标系中画出如下的图形：

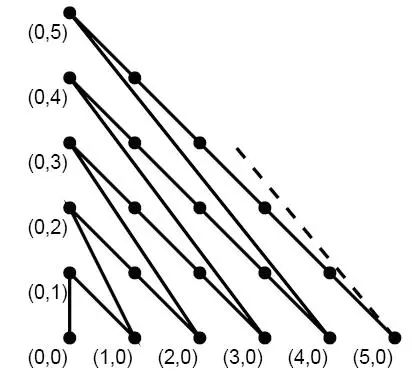
甜甜的好朋友蜜蜜发现上面的图还是有点规则的，于是他问甜甜：在你画的图中，我给你两个点，请你算一算连接两点的折线长度（即沿折线走的路线长度）吧。

Input

第一个数是正整数N（≤100）。代表数据的组数。
每组数据由四个非负整数组成x1，y1，x2，y2；所有的数都不会大于100。

Output

对于每组数据，输出两点(x1,y1),(x2,y2)之间的折线距离。注意输出结果精确到小数点后3位。

Sample Input

5
0 0 0 1
0 0 1 0
2 3 3 1
99 99 9 9
5 5 5 5

Sample Output

1.000
2.414
10.646
54985.047
0.000

思路：1.我们要求的是两点之间的距离，可以转化为点到原点的距离，然后相减。

         2.首先看这张图分为两种线：一种是有点的线【如（0，1）与（1,0）的线；（0,2）与（2,0）的线】，一种是没有点的线【如（0,1）与（0,0）的线；（0,2）与（1,0）的线，（0,3）与（2,0）的线】。

         我们先看第二种线（因为这种考虑的情况要少些）：

         A.假设要求的是（0,2）到原点的距离，最近的没有点的边那就是sqrt(pow(1,2)+pow(2,2));同理假设要求得是（0,4）到原点的距离，最近的没有点的那就是sqrt(pow(3,2)+pow(4,2)); 

         B.假设要求得是（3，0），最近的没有点的边为sqrt(pow(2,2)+pow(3,2));

         C.假设要求得 是（1,2），然后发现离该点最近的没有点的边是（0,3）与（2,0）之间的连线，1+2=3，然后也就可以像上面那样子做了。

        最后看第一种带点的线：很简单的我们可以发现第一个边为sqrt(2),第二个边为2*sqrt(2),第三个边为3*sqrt(2);

假如求得是（1,2），有1+2=3，3-1条完整的有点的边，然后根据这个点的x坐标来计算最后还有几个根号2.

代码：

#include<stdio.h>
#include<math.h>
double ll(int x,int y)
{
	int i,n=x+y;
	double s1=0,s2=0,l;
	l=(double)sqrt(2);
	for(i=0;i<n;i++)//计算的是没有点的边
	    s1=s1+sqrt(pow(i,2)+pow(i+1,2));
	for(i=1;i<n;i++)//计算的是有点的边(并且是该点之前的有点的 边)
	  s2=s2+i*l;
	s2=s2+x*l;
	s2=s2+s1;
	return s2;
}
int main()
{
	int n;
	while(scanf("%d",&n)!=EOF)
	{
	    while(n--)
	    {
	        int  x1,y1,x2,y2;
	        double sum;
	        scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
	        sum=fabs(ll(x1,y1)-ll(x2,y2));
	        printf("%.3lf\n",sum);
	    }
	}
	return 0;
}