顾险峰: 庞加莱猜测的证明和应用-技术圈


来源：中国科学院数学与系统科学研究院  

本文约4200字，建议阅读15分钟
本文为你分享顾险峰教授讲座的精彩内容。

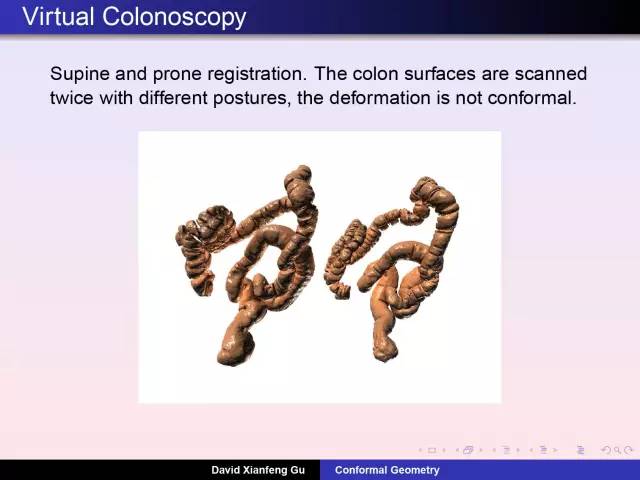
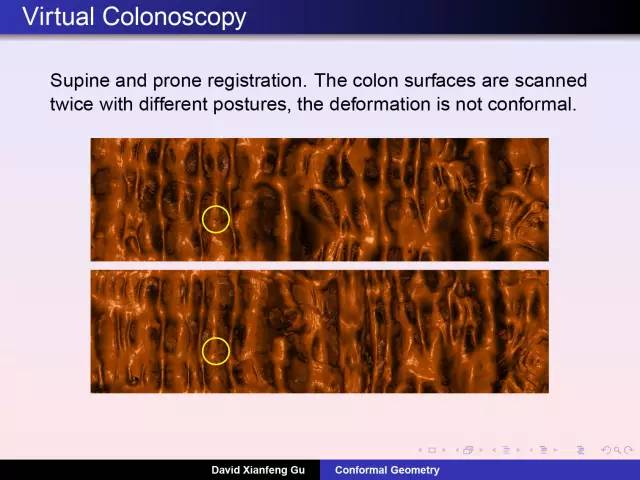
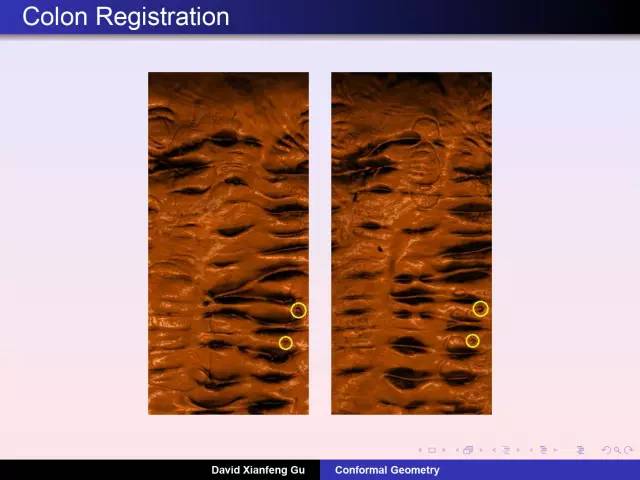
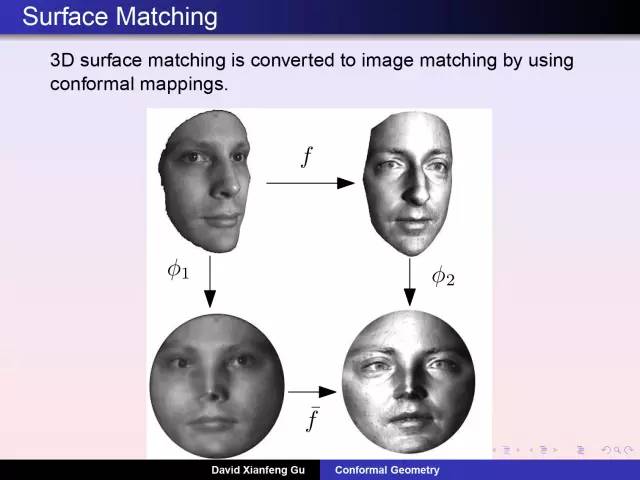
庞加莱猜测的证明，在几年前引起世人的广泛关注，更掀起中外数学界一场不小的风波。8月8日，丘成桐先生弟子顾险峰教授在知社讲坛做了题为《庞加莱猜测有用吗？》的精彩报告，从医学影像到人工智能, 从虚拟现实到物联网络, 不求八卦和恩怨, 唯有几何和民生。

首先感谢李江宇教授的邀请，感谢知社学术圈，清华校友会，海峡研究院，提供宝贵的机会和大家探讨纯粹数学的实际应用。

这些工作是在丘成桐先生的指导下，和许多数学家，计算机科学家以及医生共同完成的。

什么是庞家莱猜测？

假设曲面由橡皮膜做成，如果我们能够将其中的一个曲面不撕破，不粘连地渐变成第二个，那么我们说两个曲面具有相同的托扑。曲面的托扑由曲面具有的环柄数目（亏格）所决定，上图展示了亏格为0,1,2的不同托扑的曲面。

假设有一只具有高度智力的蚂蚁生活在曲面上。蚂蚁没有三维的概念，蚂蚁能否判别出曲面的托扑？

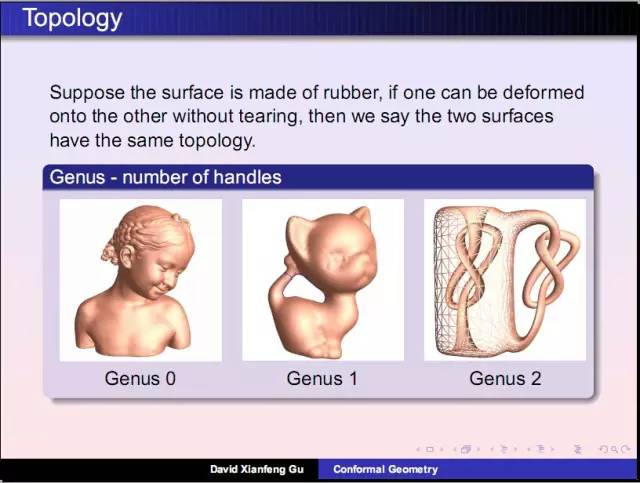
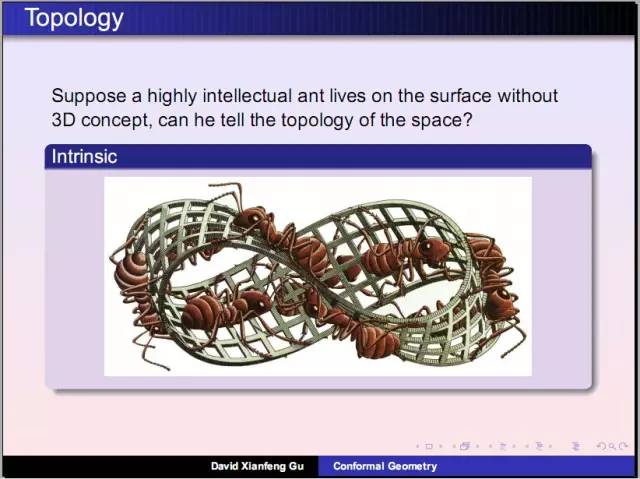
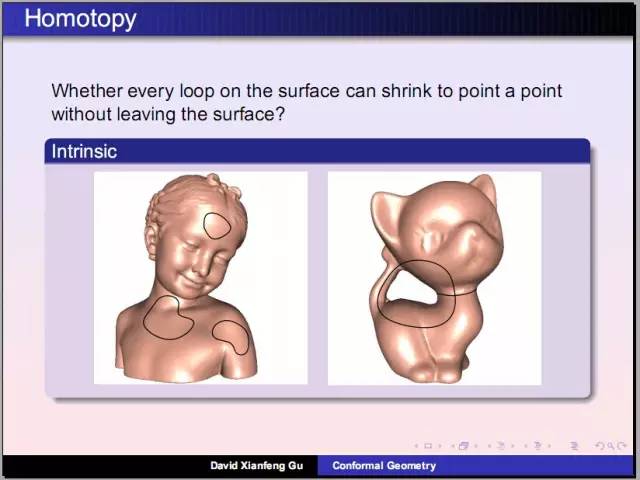
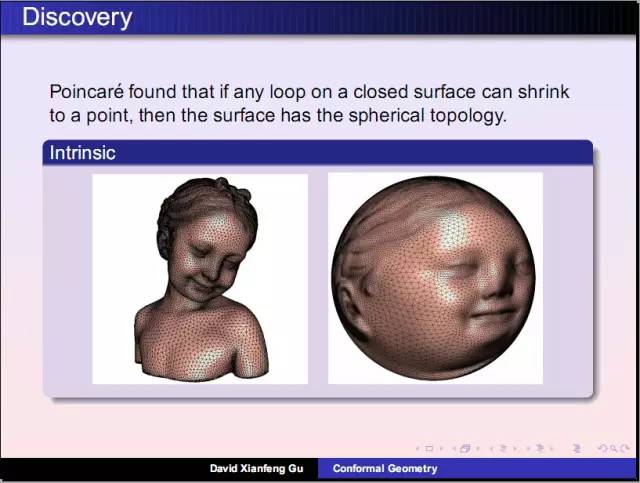
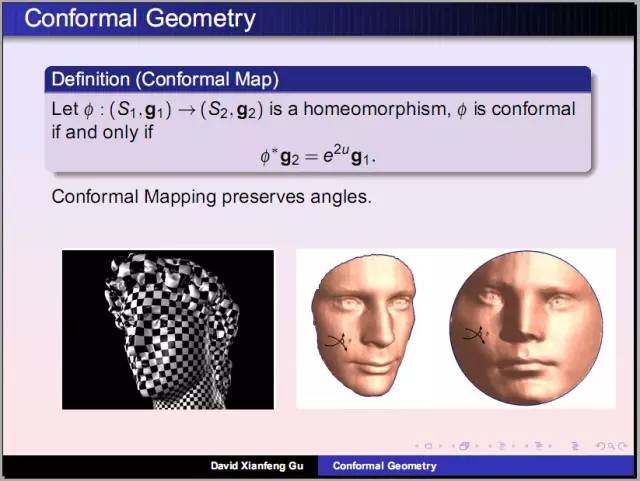
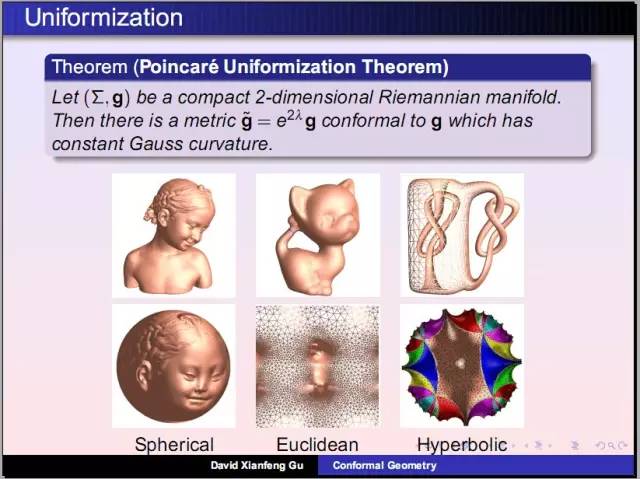
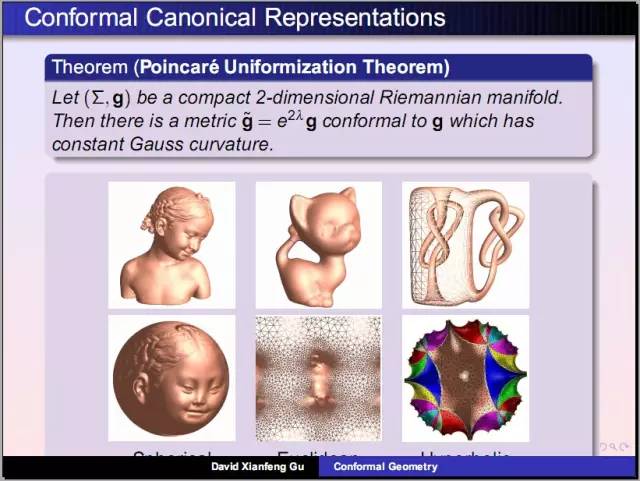
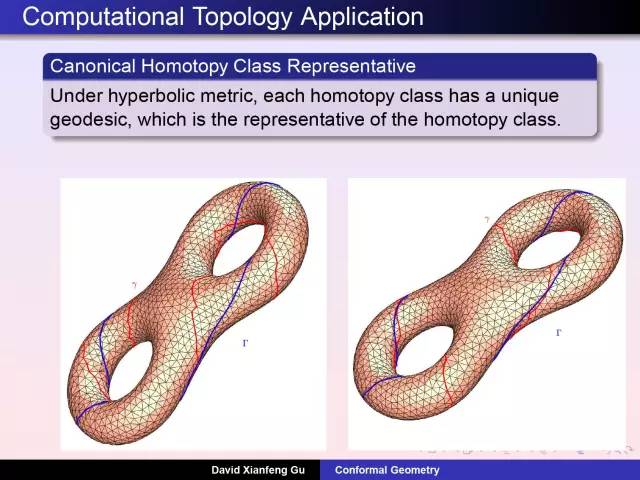
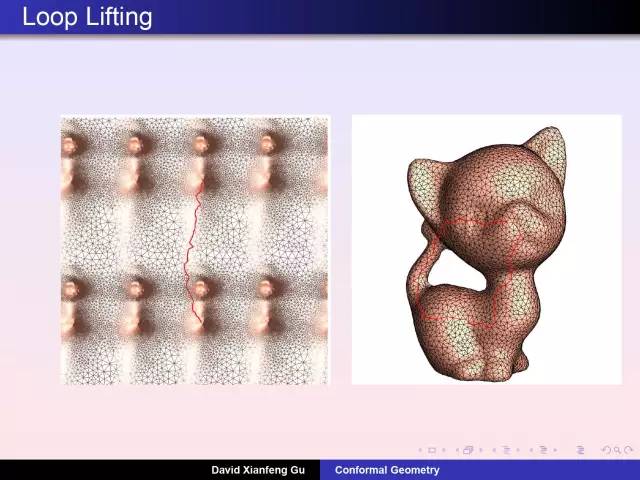
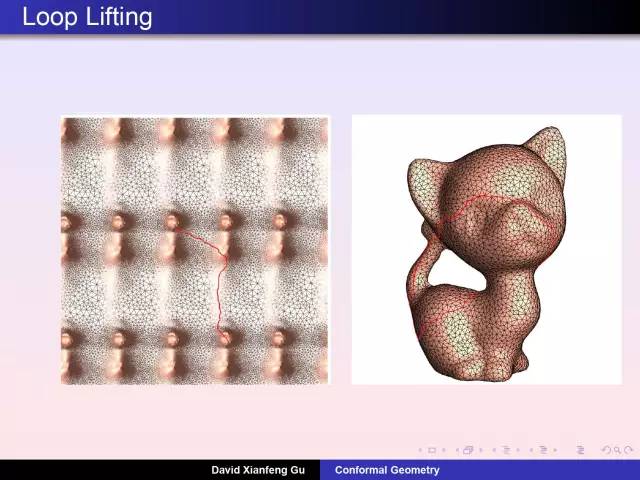
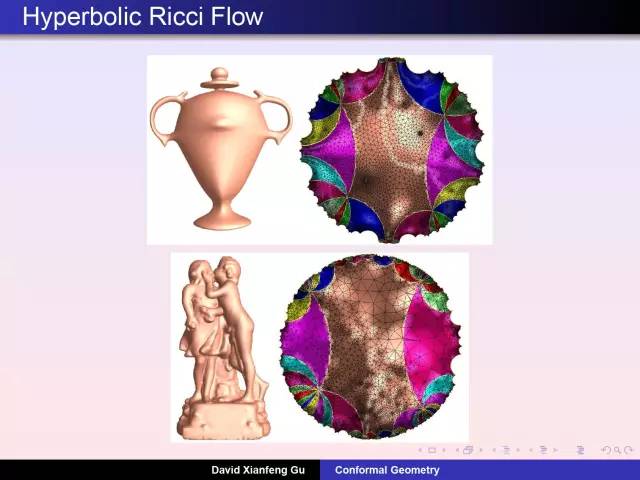
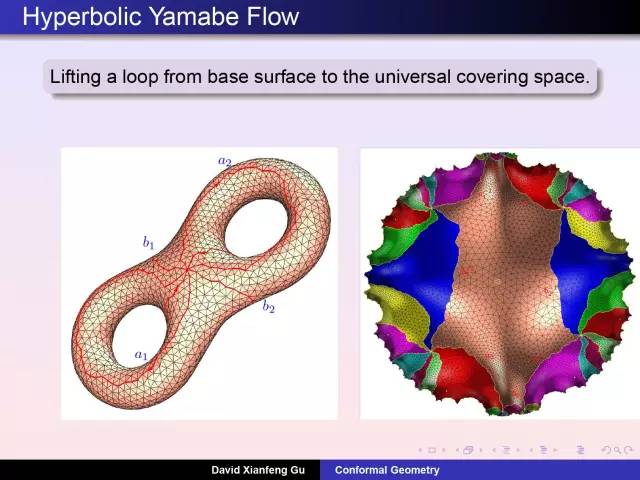
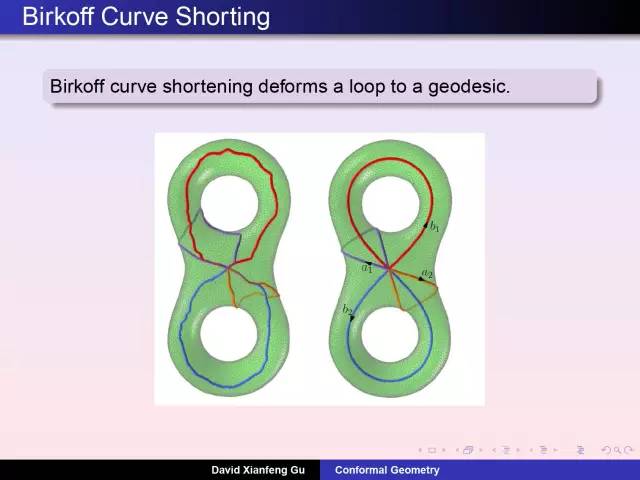
庞加莱发明了同伦理论：考察曲面上任意封闭曲线是否能够缩成一个点。女孩雕像曲面上任意圈能够缩成一个点，小猫曲面上存在这样两个圈无法缩成点。

庞加莱由此给出了一种方法：如果曲面上所有的圈都能够在曲面上渐变成一个点，则曲面亏格为零，曲面和球面托扑等价。

庞加莱将这一结论向高维推广，图中所示是一只实心的兔子，它是一个三维流形。

庞家莱猜测：单连通的三维封闭流形和三维球面托扑等价。

哈密尔顿的里奇曲率流

哈密尔顿发明了里奇曲率流的证明纲领，最终的证明由Perelman给出。数个团队补充了完整的证明细节。

视频：这里我们显示曲率流的一个可视化视频，兔子曲面和大脑皮层曲面在曲率流下变形，渐渐变成球面。

知社学术圈

哈密尔顿曲率流在曲面上的情形，黎曼度量张量随时间演化，度量张量的变化率正比于曲率，使得曲率的演化遵循非线性热流过程，直至变成常值曲率，即为球面。

陈省身大师证明过曲面上局部存在所谓的等温坐标，在等温坐标下高斯曲率具有简洁的表达式。

曲面的曲率流是共形的，或保角的：度量张量彼此相差一个标量函数。

保角变换下，曲率的变化被Yamabe方程所控制。

平面上的全纯函数是保角变换。局部形状被保持。

米开朗基罗的大卫王的雕像被保角地映到平面上面。我们看到曲面的保角变换保持局部形状。

共形变换的微分几何定义，以及几何直观。

共形变换保持角度，同时将无穷小圆映到无穷小圆。

一般的微分同胚，将无穷小圆映到无穷小椭圆。

曲面的曲率流推出所谓的单值化定理：任意封闭的度量曲面都能够保角地变换成常曲率曲面，球面，欧式平面或双曲曲面。换言之，曲面可以允许三种几何中的一种：球面，欧式或双曲几何。这一定理的三维推广就是瑟斯顿猜测：任何三维流形都可以被分解为素流形，每个素流形允许八种几何中的一种。

哈密尔顿的曲率流在曲面上形态良好，不会产生奇异点；在三流形上，有限时间内，流形上可能产生爆破点，在这些点处，曲率变成无穷大。我们将流形沿着爆破点切开，每个连通分支接着运行曲率流。这叫做对三流形的“手术”。我们需要证明，在整个流的过程中，产生的爆破点是有限的。

在座的有些高中同学，我们用离散的语言解释一下，精神实质是相同的。我们用多面体网格来逼近光滑曲面，它们由三角面片粘合而成。每个三角面片可以是欧式三角形，球面三角形或双曲三角形。

我们为每条边附上一个正数，使得在任意三角面片上三角形不等式成立，这样一个赋值就是一个离散黎曼度量。如果我们保持组合结构不变，可以有无穷多个离散黎曼度量。

曲率是衡量曲面局部上和平面之间的差异，所以可以用“角欠”来表示。离散情形下，高斯-博内定理依然成立。

连续情况下黎曼度量决定高斯曲率，离散情况下，三角形边长决定内角。边角关系由余弦定理来表示。

离散的共形变换比较复杂，我们的想法来自于共形变换的保圆性：无穷小圆映到无穷小圆。

瑟斯顿提议如下的方法：给定平面区域，我们将其三角剖分，在定点处放置圆盘。每条边上的两个圆盘彼此相切。然后我们改变圆盘半径，保持三角剖分的组合关系，和圆盘间的相切关系，三角剖分覆盖的区域随之发生变化。初始三角剖分，和最终三角剖分的区域间建立了分片线性映射。如果三角剖分逐步加细，直至无穷，则分片线性映射收敛到光滑的共形变换。

我们建立了离散曲率流的方程，这里u是半径的对数。哈密尔顿发明了曲率流，Perelman发现曲率流是某种特定能量的梯度流，所谓的“熵”。离散的“熵”能量是凸能量，因此我们可以应用牛顿法来优化。

我们用离散曲面曲率流方法计算曲面的单值化。

带边曲面的单值化非常类似，每个边界被映成常曲率空间中的圆。

应用

医学图像领域的应用。

大脑皮层曲面，及主要的功能区域。

我们将大脑皮层用曲率流共形地映到球面上，从而为大脑表面的每一点精确建立坐标。

这种“共形脑图”适用于大脑皮层曲面的注册，匹配和比较。

大脑皮层曲面上有一些显著的沟回，我们沿着这些沟回切开，再用曲率流映到平面多孔圆盘上。

通过建立大脑皮层间的映射，我们可以追踪大脑萎缩的模式，正常大脑老化，皮层收缩是各向同性的。一些疾病会诱发各向异性的萎缩。

有些神经疾病会诱发沟回变厚，我们定期扫描病人的大脑，追踪皮层沟回的厚度变化以帮助诊断。

最优传输理论：平面区域上给定两个概率密度，存在保测度的自映射。在所有保测度的映射中，使得传输代价最小者被称为是最优传输映射。最优传输映射的传输代价被称为是两个概率密度之间的Wasserstein距离。

比如，我们考虑一个国家的马铃薯亩产率和消耗率，这给出了两个概率密度函数。政府设计一套马铃薯的运输方案，使得处处供销平衡，同时极小化全国的运输成本，这等价于求最优传输。Kontarovich凭借这一理论赢得了诺贝尔经济奖。

Wasserstein距离的计算依赖于解非线性的蒙日-安培偏微分方程。这一方程曾被丘成桐先生应用于理论物理领域，获得了菲尔茨奖。蒙日-安培方程的解给出了最优传输映射，从而得到Wasserstein距离。

我们设计了实验，扫描了上百人的大脑皮层曲面，测试了他们的智商，用曲率流方法将大脑皮层映射到单位球面上。从而将大脑皮层的黎曼度量转化为球面上的概率密度。

我们将这些大脑依照智商排序，并用像素的灰度值表示两个大脑间的Wasserstein几何距离，我们看到，靠近对角线的区域，颜色较暗，远离对角线的区域，颜色较亮。这意味着智商距离和几何距离相一致。在一定程度上，大脑形状反映了智商。

虚拟肠镜：直肠癌是男子的第四号杀手，一般由直肠息肉演变而来。发现并监控直肠息肉是最为有效的防治方法。传统的光学肠镜方法医生和病人有肢体接触，具有一定的侵犯性。病人需要被全身麻醉，容易诱发并发症。虚拟肠镜用CT技术采集病人的直肠几何曲面，并用曲率流的方法将直肠曲面展开摊平，将肠曲面上的所有皱褶打开，暴漏所有的息肉。同时对于从不同姿态获取的直肠曲面可以建立精确的映射，以提高诊断准确率。