Python数学建模系列（五）：微分方程
海轰Pro
共 15050字，需浏览 31分钟
· 2021-09-01
1、微分方程分类
微分方程是用来描述某一类函数与其导数之间关系的方程，其解是一个符合方程的函数。
微分方程按自变量个数可分为常微分方程和偏微分方程
常微分方程（ODE：ordinary differential equation）
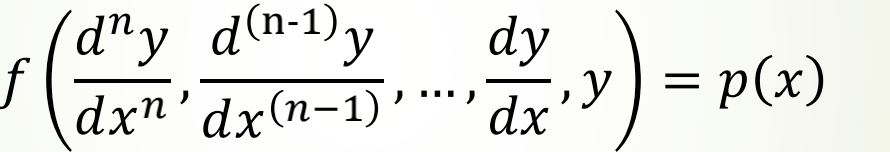
偏微分方程（两个以上的自变量）
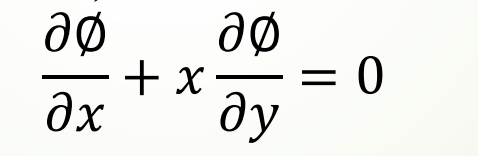
2、微分方程解析解
具备解析解的ODE（常微分方程），我们可以利用SymPy库进行求解
以求解阻尼谐振子的二阶ODE为例，其表达式为：
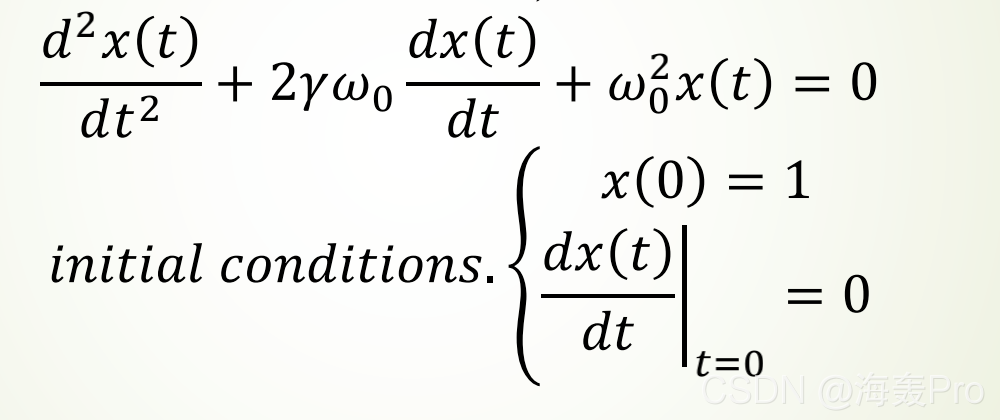
Demo代码
import sympy
def apply_ics(sol, ics, x, known_params):
free_params = sol.free_symbols - set(known_params)
eqs = [(sol.lhs.diff(x, n) - sol.rhs.diff(x, n)).subs(x, 0).subs(ics) for n in range(len(ics))]
sol_params = sympy.solve(eqs, free_params)
return sol.subs(sol_params)
# 初始化打印环境
sympy.init_printing()
# 标记参数，且均为正
t, omega0, gamma = sympy.symbols("t, omega_0, gamma", positive=True)
# 标记x是微分函数，非变量
x = sympy.Function("x")
# 用diff()和dsolve得到通解
# ode 微分方程等号左边的部分，等号右边为0
ode = x(t).diff(t, 2) + 2 * gamma * omega0 * x(t).diff(t) + omega0 ** 2 * x(t)
ode_sol = sympy.dsolve(ode)
# 初始条件：字典匹配
ics = {x(0): 1, x(t).diff(t).subs(t, 0): 0}
x_t_sol = apply_ics(ode_sol, ics, t, [omega0, gamma])
sympy.pprint(x_t_sol)
运行结果：
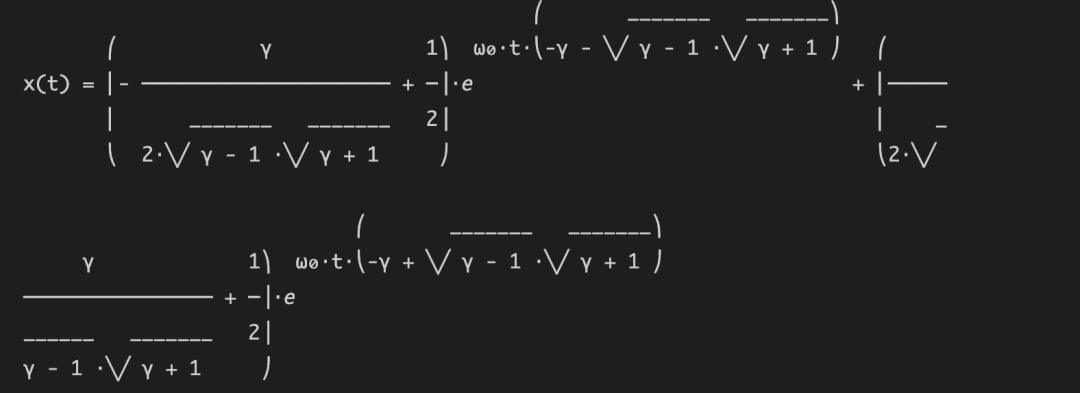
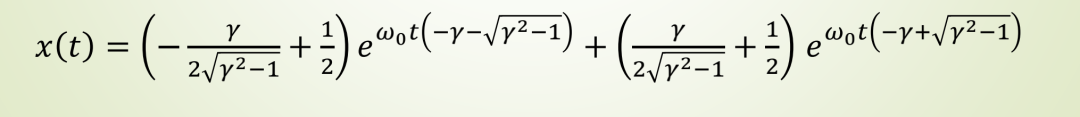
3、微分方程数值解
当ODE无法求得解析解时，可以用scipy中的integrate.odeint求 数值解来探索其解的部分性质,并辅以可视化，能直观地展现 ODE解的函数表达。
以如下一阶非线性（因为函数y幂次为2）ODE为例：
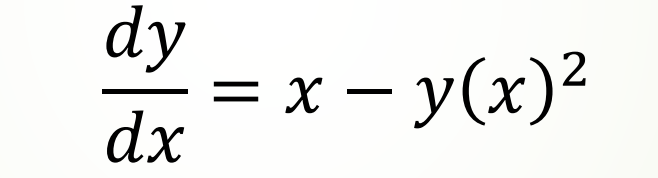
现用odeint求其数值解
3.1 场线图与数值解
Demo代码
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
import sympy
def plot_direction_field(x, y_x, f_xy, x_lim=(-5, 5), y_lim=(-5, 5), ax=None):
f_np = sympy.lambdify((x, y_x), f_xy, 'numpy')
x_vec = np.linspace(x_lim[0], x_lim[1], 20)
y_vec = np.linspace(y_lim[0], y_lim[1], 20)
if ax is None:
_, ax = plt.subplots(figsize=(4, 4))
dx = x_vec[1] - x_vec[0]
dy = y_vec[1] - y_vec[0]
for m, xx in enumerate(x_vec):
for n, yy in enumerate(y_vec):
Dy = f_np(xx, yy) * dx
Dx = 0.8 * dx**2 / np.sqrt(dx**2 + Dy**2)
Dy = 0.8 * Dy*dy / np.sqrt(dx**2 + Dy**2)
ax.plot([xx - Dx/2, xx + Dx/2], [yy - Dy/2, yy + Dy/2], 'b', lw=0.5)
ax.axis('tight')
ax.set_title(r"$%s$" %(sympy.latex(sympy.Eq(y_x.diff(x), f_xy))), fontsize=18)
return ax
x = sympy.symbols('x')
y = sympy.Function('y')
f = x-y(x)**2
f_np = sympy.lambdify((y(x), x), f)
## put variables (y(x), x) into lambda function f.
y0 = 1
xp = np.linspace(0, 5, 100)
yp = integrate.odeint(f_np, y0, xp)
## solve f_np with initial conditons y0, and x ranges as xp.
xn = np.linspace(0, -5, 100)
yn = integrate.odeint(f_np, y0, xn)
fig, ax = plt.subplots(1, 1, figsize=(4, 4))
plot_direction_field(x, y(x), f, ax=ax)
## plot direction field of function f
ax.plot(xn, yn, 'b', lw=2)
ax.plot(xp, yp, 'r', lw=2)
plt.show()
运行结果：
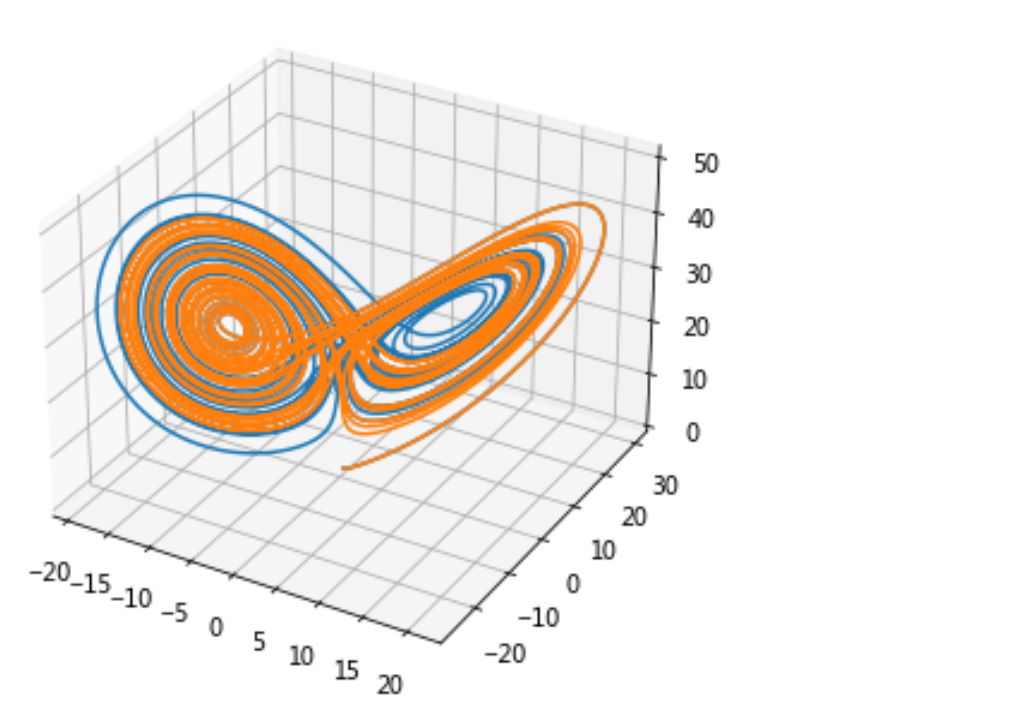
3.2 洛伦兹曲线与数值解
以求解洛伦兹曲线为例，以下方程组代表曲线在xyz三个方向 上的速度，给定一个初始点，可以画出相应的洛伦兹曲线：
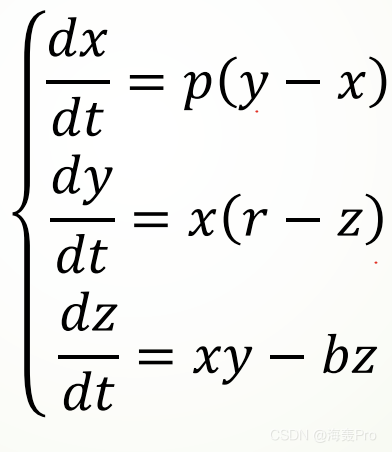
Demo代码
import numpy as np
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
def dmove(Point, t, sets):
p, r, b = sets
x, y, z = Point
return np.array([p * (y - x), x * (r - z), x * y - b * z])
t = np.arange(0, 30, 0.001)
P1 = odeint(dmove, (0., 1., 0.), t, args=([10., 28., 3.],))
P2 = odeint(dmove, (0., 1.01, 0.), t, args=([10., 28., 3.],))
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(P1[:, 0], P1[:, 1], P1[:, 2])
ax.plot(P2[:, 0], P2[:, 1], P2[:, 2])
plt.show()
运行结果：
4、传染病模型
模型一：SI-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt
# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# T为传播时间
T = 150
# INI为初始状态下的数组
INI = (S_0,I_0)
def funcSI(inivalue,_):
Y = np.zeros(2)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[1]) / N + gamma * X[1]
# 感染个体变化
Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
return Y
T_range = np.arange(0,T + 1)
RES = spi.odeint(funcSI,INI,T_range)
plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.title('SI Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()
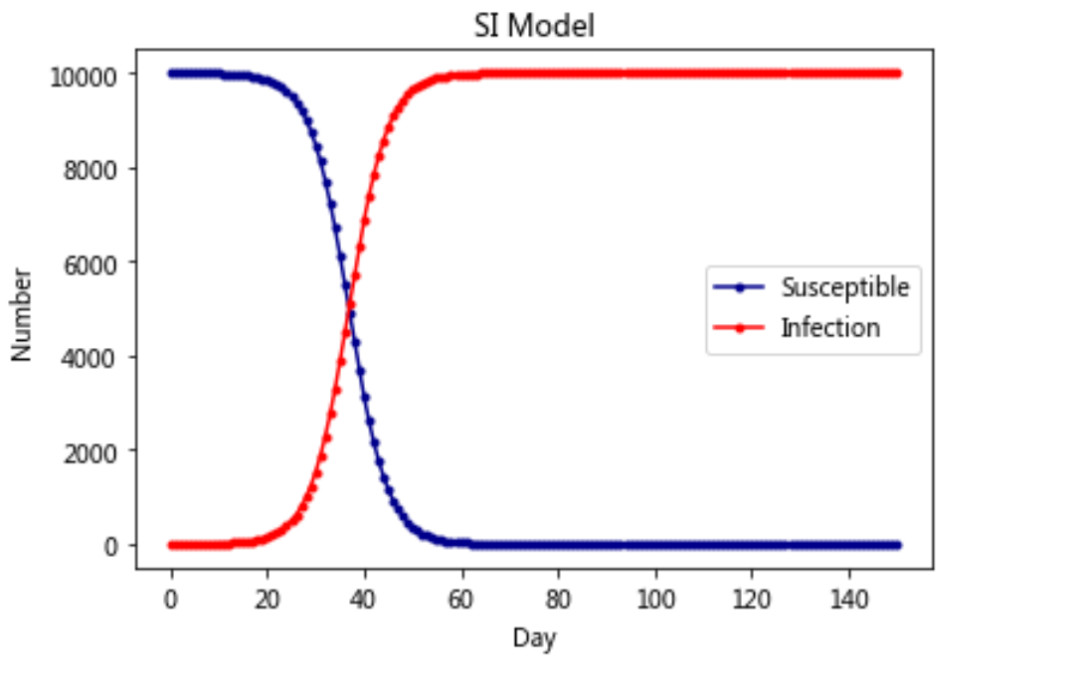
模型二：SIS model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt
# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# T为传播时间
T = 150
# INI为初始状态下的数组
INI = (S_0,I_0)
def funcSIS(inivalue,_):
Y = np.zeros(2)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0]) / N * X[1] + gamma * X[1]
# 感染个体变化
Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
return Y
T_range = np.arange(0,T + 1)
RES = spi.odeint(funcSIS,INI,T_range)
plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.title('SIS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()
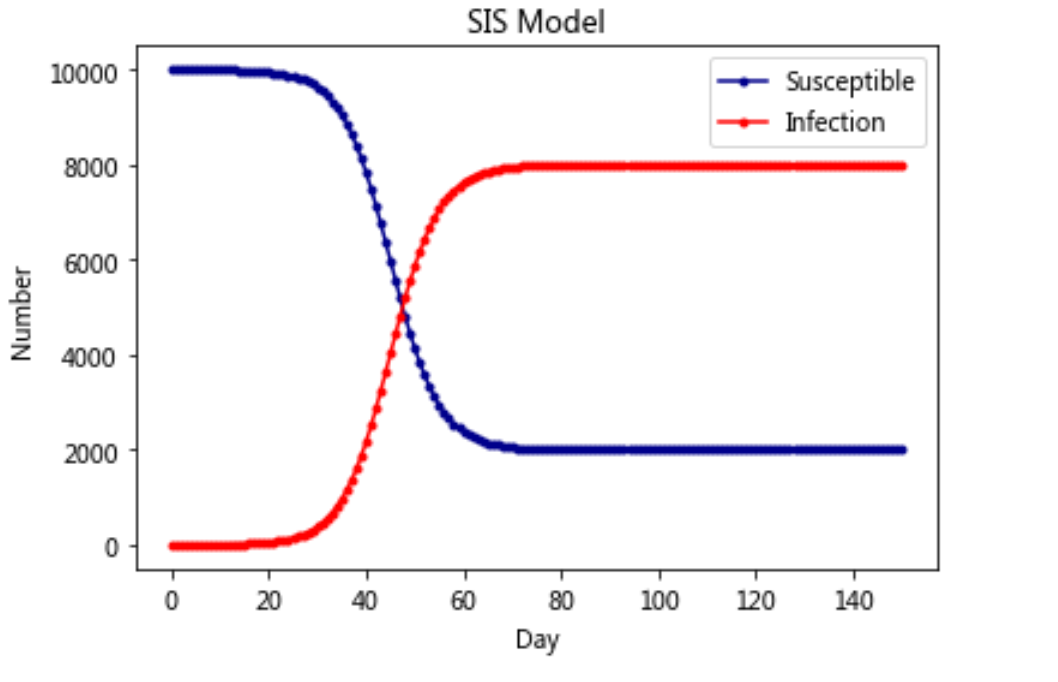
模型三：SIR model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt
# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - R_0
# T为传播时间
T = 150
# INI为初始状态下的数组
INI = (S_0,I_0,R_0)
def funcSIR(inivalue,_):
Y = np.zeros(3)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[1]) / N
# 感染个体变化
Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
# 治愈个体变化
Y[2] = gamma * X[1]
return Y
T_range = np.arange(0,T + 1)
RES = spi.odeint(funcSIR,INI,T_range)
plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,2],color = 'green',label = 'Recovery',marker = '.')
plt.title('SIR Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()
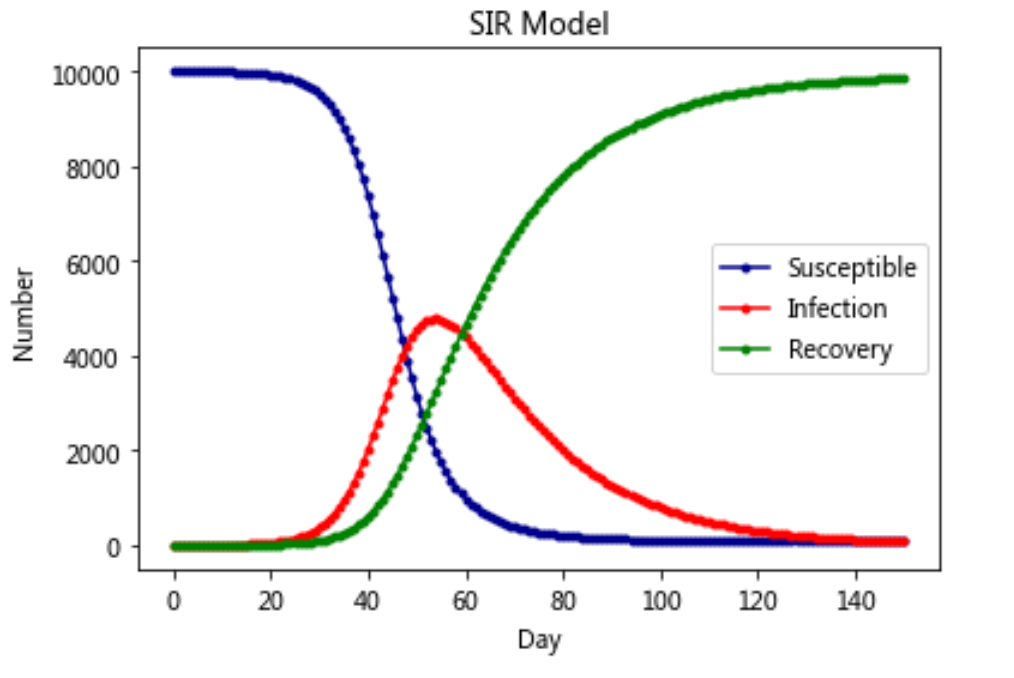
模型四：SIRS-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt
# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# Ts为抗体持续时间
Ts = 7
# I_0为感染者的初始人数
I_0 = 1
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - R_0
# T为传播时间
T = 150
# INI为初始状态下的数组
INI = (S_0,I_0,R_0)
def funcSIRS(inivalue,_):
Y = np.zeros(3)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[1]) / N + X[2] / Ts
# 感染个体变化
Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
# 治愈个体变化
Y[2] = gamma * X[1] - X[2] / Ts
return Y
T_range = np.arange(0,T + 1)
RES = spi.odeint(funcSIRS,INI,T_range)
plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,2],color = 'green',label = 'Recovery',marker = '.')
plt.title('SIRS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()
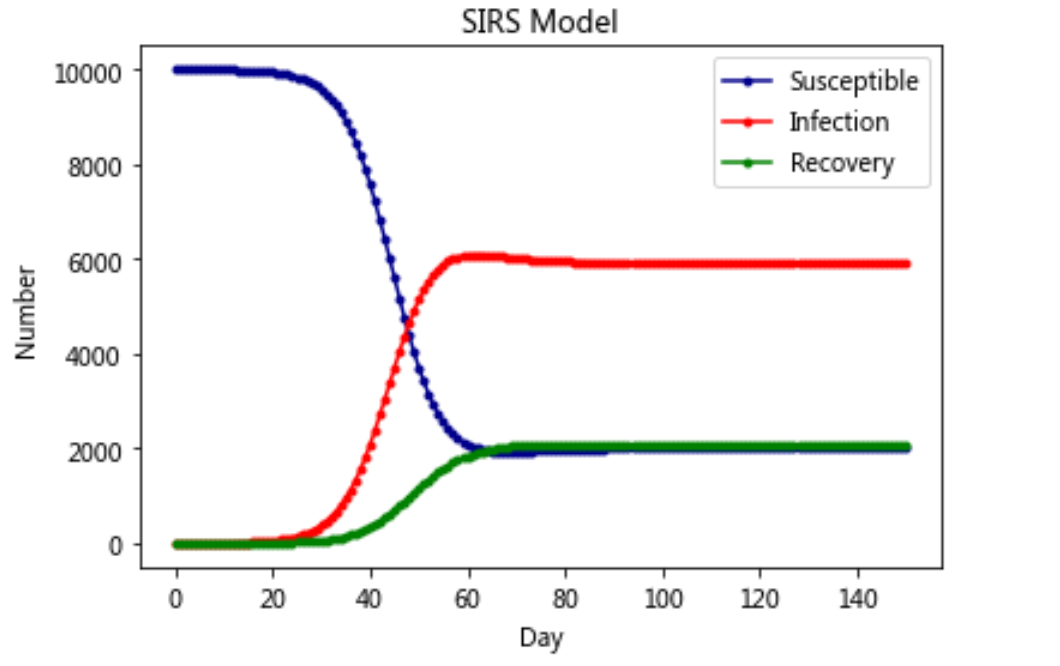
模型五：SEIR-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt
# N为人群总数
N = 10000
# β为传染率系数
beta = 0.6
# gamma为恢复率系数
gamma = 0.1
# Te为疾病潜伏期
Te = 14
# I_0为感染者的初始人数
I_0 = 1
# E_0为潜伏者的初始人数
E_0 = 0
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - E_0 - R_0
# T为传播时间
T = 150
# INI为初始状态下的数组
INI = (S_0,E_0,I_0,R_0)
def funcSEIR(inivalue,_):
Y = np.zeros(4)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[2]) / N
# 潜伏个体变化
Y[1] = (beta * X[0] * X[2]) / N - X[1] / Te
# 感染个体变化
Y[2] = X[1] / Te - gamma * X[2]
# 治愈个体变化
Y[3] = gamma * X[2]
return Y
T_range = np.arange(0,T + 1)
RES = spi.odeint(funcSEIR,INI,T_range)
plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'orange',label = 'Exposed',marker = '.')
plt.plot(RES[:,2],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,3],color = 'green',label = 'Recovery',marker = '.')
plt.title('SEIR Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()
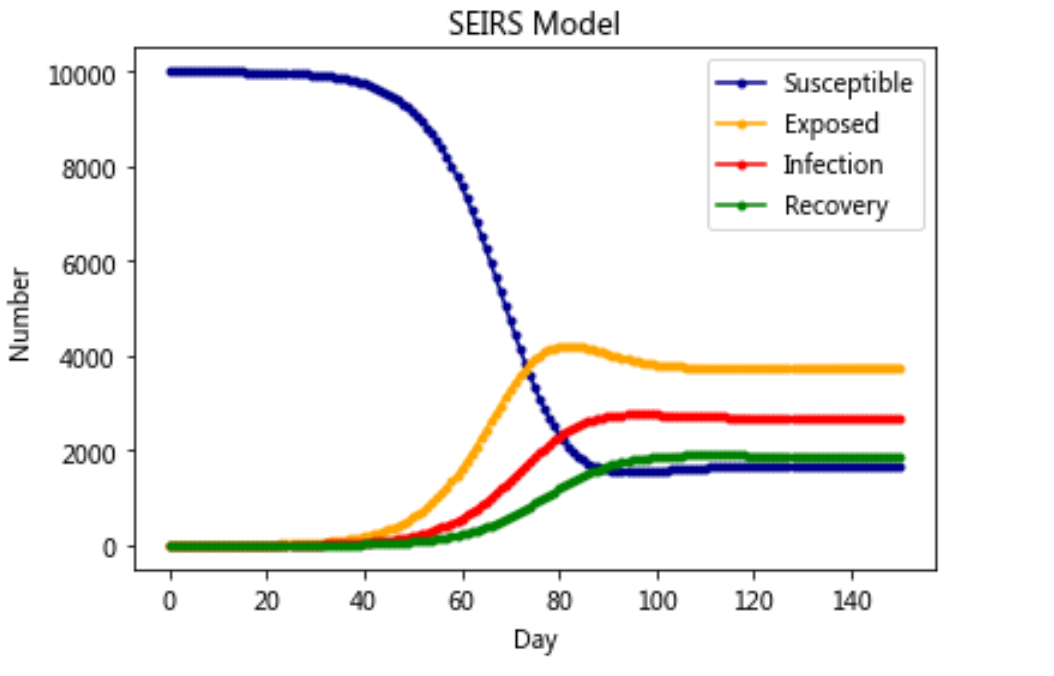
模型六：SEIRS-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt
# N为人群总数
N = 10000
# β为传染率系数
beta = 0.6
# gamma为恢复率系数
gamma = 0.1
# Ts为抗体持续时间
Ts = 7
# Te为疾病潜伏期
Te = 14
# I_0为感染者的初始人数
I_0 = 1
# E_0为潜伏者的初始人数
E_0 = 0
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - E_0 - R_0
# T为传播时间
T = 150
# INI为初始状态下的数组
INI = (S_0,E_0,I_0,R_0)
def funcSEIRS(inivalue,_):
Y = np.zeros(4)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[2]) / N + X[3] / Ts
# 潜伏个体变化
Y[1] = (beta * X[0] * X[2]) / N - X[1] / Te
# 感染个体变化
Y[2] = X[1] / Te - gamma * X[2]
# 治愈个体变化
Y[3] = gamma * X[2] - X[3] / Ts
return Y
T_range = np.arange(0,T + 1)
RES = spi.odeint(funcSEIRS,INI,T_range)
plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'orange',label = 'Exposed',marker = '.')
plt.plot(RES[:,2],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,3],color = 'green',label = 'Recovery',marker = '.')
plt.title('SEIRS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()
结语
参考：
https://www.bilibili.com/video/BV12h411d7Dm https://zhuanlan.zhihu.com/p/104091330
学习来源：
B站及其课堂PPT 对其中代码进行了复现
「文章仅作为学习笔记，记录从0到1的一个过程」
希望对您有所帮助，如有错误欢迎小伙伴指正～
评论
金融研究 | 使用Python测量关键审计事项的「信息含量」
Tips: 公众号推送后内容只能更改一次，且只能改20字符。如果内容出问题，或者想更新内容， 只能重复推送。为了更好的阅读体验，建议阅读本文博客版， 链接地址https://textdata.cn/blog/2023-01-13-information-content-of-critical-aud
大邓和他的Python
0
金融研究(更新) | 使用Python构建关键审计事项的「信息含量」
Tips: 公众号推送后内容只能更改一次，且只能改20字符。如果内容出问题，或者想更新内容， 只能重复推送。为了更好的阅读体验，建议阅读本文博客版， 链接地址https://textdata.cn/blog/2023-01-13-information-content-of-critical-aud
大邓和他的Python
0
谷歌员工爆料 Python 基础团队原地解散
转自 | 机器之心编辑 | 蛋酱什么？谷歌解雇了整个 Python 基础团队？「当与你直接共事的每个人，包括你的主管，都被裁员 —— 哦，是职位被削减，而你被要求安排他们的替代者入职，这些人被告知在不同的国家担任同样的职位，但他们并不为此感到高兴，这是很艰难的一天。」发布这一动态的 Tho
机器学习算法与Python实战
0
五一抢票难，Github上这几个Python项目，你可以试试
又到五一长假啦（虽然其实就放了1天），大家是打算家里蹲or出去玩，又或者是在公司加班呢...今天给大家介绍三个和12306相关的项目，看看你是否用得上。/01/ py12306py12306购票助手，顾名思义，12306买票的~需要在python 3.6以上版本运行程序。1. 安装依赖gi
Crossin的编程教室
0
谷歌员工爆料Python基础团队原地解散
机器之心报道编辑：蛋酱什么？谷歌解雇了整个 Python 基础团队？「当与你直接共事的每个人，包括你的主管，都被裁员 —— 哦，是职位被削减，而你被要求安排他们的替代者入职，这些人被告知在不同的国家担任同样的职位，但他们并不为此感到高兴，这是很艰难的一天。」发布这一动态的 Thomas Wouter
机器学习初学者
0
Python加速运行技巧
Python 是一种脚本语言，相比 C/C++ 这样的编译语言，在效率和性能方面存在一些不足。但是，有很多时候，Python 的效率并没有想象中的那么夸张。本文对一些 Python 代码加速运行的技巧进行整理。 0. 代码优化原则 本文会介绍不少的 Python 代码加速运行的技巧。在深入代码优化细
机器学习算法与Python实战
0
Go 1.22 的新增功能系列之二：reflect.TypeFor
Go 1.22 的第一个候选版本已经发布，这意味着最终版本即将发布，现在是我在博客中介绍我在这个周期中所做工作的时候了。像往常一样，我的贡献很小，但它们是我的，所以我将从幕后的角度来谈谈它们。首先是reflect.TypeFor。这是整个函数：// TypeFor returns the [Type
GoCN
0
为什么我们公司还在用 Python 开发项目?
作者：哇哒嘻哇https://www.zhihu.com/question/278798145/answer/3416549119最近几年里，经常看到某些曾重度使用 Python 的大公司迁移成其它语言技术栈，但是，那些小公司/小团队的情况如何呢？一直很想了解那些仍在坚持使用 Python，且支撑业
机器学习算法与Python实战
0