LeetCode 11:用递归和动规解决正则表达式匹配
这道题,貌似考过挺多次,之前在笔试时,也遇到过类似的变形题,有点小难度。
题目描述
给定一个字符串 (s) 和一个字符模式 (p)。实现支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
'.' 匹配任意单个字符。
'*' 匹配零个或多个前面的元素。
匹配应该覆盖整个字符串 (s) ,而不是部分字符串。
说明:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
示例 1:
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:
s = "aa"
p = "a*"
输出: true
解释: '*' 代表可匹配零个或多个前面的元素,
即可以匹配 'a' 。因此, 重复 'a' 一次, 字符串可变为 "aa"。
示例 3:
输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 'c' 可以不被重复, 'a' 可以被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false
题解
我之前没怎么学过正则表达式,刚开始居然有点看不懂是什么意思,,这就尴尬了,可能也有一些人和我一样的,所以我就啰嗦一点解释下
‘*‘匹配零个或多个前面的元素
这句话的具体意思……,可能你们没有这样的疑问,但我还是要说下,就是说,* 的功能,可以把 * 号前面的一个字符当做n个字符来使用(貌似我说和没说一样…)。举个例子,例如字符串 ab*,那么这个字符串可以表示为 a,或者ab,或者 abbbb(n个b)。
刚开始用递归的方式做,相对容易点,由于挺多细节,虽然知道思路,加上挺久没做算法题,所以也是花了不少时间。之后用动态规划的方法做,相对难点,不过通过这道题的考验,感觉对动态规划的掌握,又更熟练了。
下面简单讲解下思路:
方法1:递归
递归看的懂但自己又写不出代码的,可以看我之前的文章:为什么你学不会递归?告别递归,谈谈我的一些经验
首先,先考虑特殊情况
(1).如果两个字符串都为空,返回true
(2).当第一个字符串不空,而第二个字符串空了,返回false
可能有人会问如果 p 不为空,而s为空,那要返回 false 吗?答是不一定,因为 a* 可以充当空字符串。
下面就是正常情况的匹配了。在比较字符的过程中,如果 p 的下一个字符为 * 或不为 *,那么会出现不同的情况。下面我们分两种情况来讨论。
(a). 如果下一个字符不为 *:这种情况比较简单,直接匹配当前字符。如果匹配成功,继续匹配下一个;如果匹配失败,直接返回 false。
(b). 如果 p 的下一个字符为 * 时,稍微复杂一些,因为 * 可以代表0个或多个。所以又得分成三种情况来讨论:
1). 当 * 匹配 0 个字符时,s 当前字符不变,p 当前字符后移两位,相当于跳过到 * 符号后面来匹配;
2). 当 * 匹配 1 个时,s 当前字符向后移动 1 位,p 当前字符 向后移动 2 位。
3). 当 * 匹配多个时,s 当前字符向后移动 1 为,p 当前字符不移动。
直接上代码,代码里也有详细的解释
其代码如下:(可以左右拉动,下面也有图片版)
public boolean isMatch(String s, String p) {
if(s == null || p == null)
return false;
if(s.length() >= 1 && p.length() < 1)
return false;
int i = 0;
int j = 0;
return match(s, i, p, j);
}
public boolean match(String s, int i, String p, int j){
//先验证是否匹配结束
//同时都到结尾了
if(i >= s.length() && j >= p.length())
return true;
//s还没结尾,但p到达结尾了
if(i < s.length() && j >= p.length())
return false;
//如果下一个字符不是*,或者这个字符就是最后一个字符了,则直接匹配
if(j+1'*' || p.length()==j+1){
if(i'.'))
return match(s,i+1, p, j+1);
else
return false;
}else{
//下一个字符是*,则分为两种种情况
//1.如果当前字符不匹配(或者s已经越界了),
// 则p字符移动2位,而s不移动
if((i'.') || i == s.length())
return match(s, i, p, j+2);
//2.如果当前字符匹配的话,分两种情况讨论
else{
//(1).匹配0个字符,则p直接移动2位,s不移动
//(2).匹配一个,s移动一位,p移动两位
//(3),匹配多个,s移动一位,p不移动
return match(s, i, p, j+2) || match(s, i+1, p, j) ||
match(s, i+1, p, j+2);
}
}
}
方便阅读,图片版本
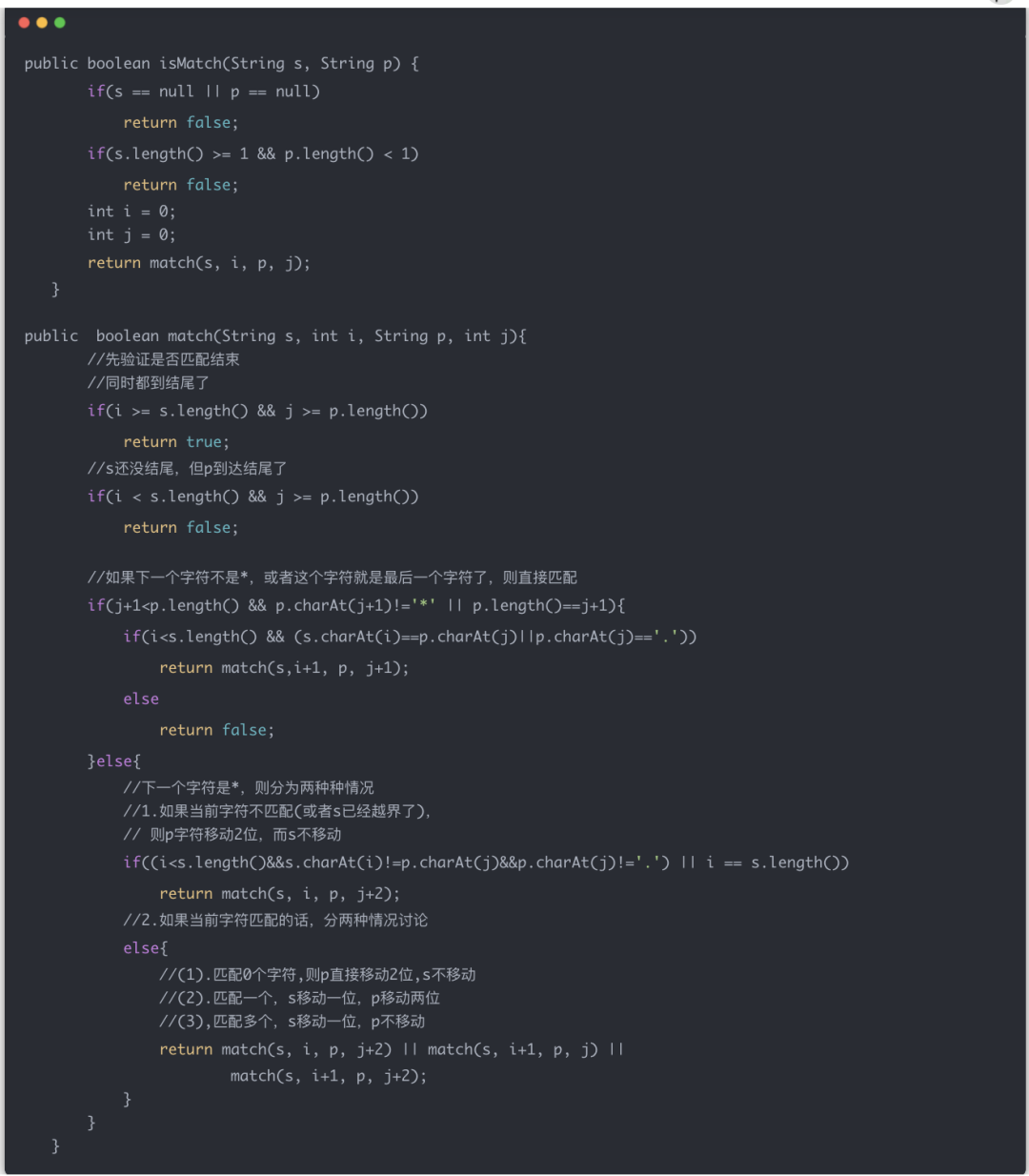
实际上我们也是可以把匹配一个当作匹配多个来处理的,匹配一个等价于 先匹配多个,再匹配 0 个。
不过这种递归方法比较低效,类似于暴力递归,时间复杂度都指数了,优化的方法可以用一个数组来进行状态保持,下面用动态规划来做,其实动态规划,有时候就是等价于 递归 + 状态保存,当时,我说的是有时候。
方法2:动态规划
接下来用dp(动态规划)来做,不过这个我就不详细讲了。直接上代码了,不过代码里有些关键的地方有解释。DP 的我也有写过两篇,知乎 8000 多点赞写过,大家有兴趣的可以看下告别动态规划,连刷40道动规算法题,我总结了动规的套路
不过如果你们理解了上面递归的做法,那么感觉这个 dp 的也还是不难懂的
public boolean isMatch1(String s, String p){
if(s == null || p == null)
return false;
int len_s = s.length();
int len_p = p.length();
//存放状态
boolean[][]dp = new boolean[len_s+1][len_p+1];
//初始化
dp[0][0] = true;
for(int i = 1; i <= len_p; i++){
if(p.charAt(i-1) == '*')
dp[0][i] = dp[0][i-2];
}
for(int i = 1; i <= len_s; i++){
for(int j = 1; j <= len_p; j++){
//如果不为‘*’且匹配
if(p.charAt(j-1)=='.'||p.charAt(j-1)==s.charAt(i-1))
dp[i][j] = dp[i-1][j-1];
//如果是*
else if(p.charAt(j-1)=='*'){
//如果p中*号前面的字符与s当前字符不匹配,则匹配0个
if(j!=1&&p.charAt(j-2)!='.'&&p.charAt(j-2)!=s.charAt(i-1)){
dp[i][j] = dp[i][j-2];
}else{
//否则有三种情况:
//匹配0个,匹配1个,匹配多个
dp[i][j] = dp[i][j-2] || dp[i][j-1]||dp[i-1][j];
}
}
}
}
return dp[len_s][len_p];
}
图片版本
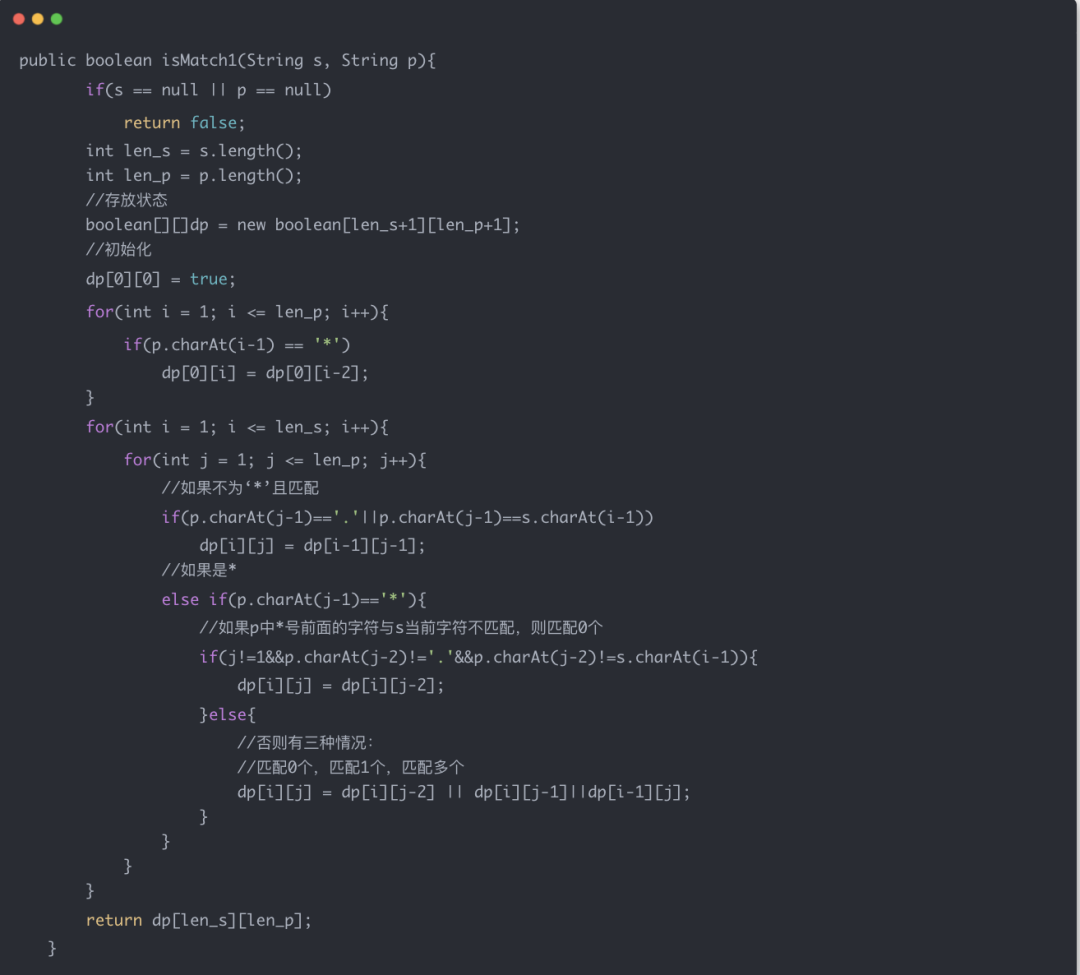
后面可能会更剑指 offer 和 leetcode top 100 的文章,你们有想看的也可以留言说,不过后面的文章,为了方便大家阅读,主要还是会放在我的网站上,我的空网站即将横空出世。
