为什么 AI 犯的错有时会很“瘆人”?

(一) 光头的诱惑




(二) 机器学习出了什么问题?


1、给数据集扩容;
2、安排超高性能的计算设备;(用于训练 GPT-3 的计算机,拥有 285000 个 CPU 内核、10000 个 GPU 和 400Gbps 的网络连接,位列全球超级计算机榜第 5 位。)
3、钻研复杂精深的算法。



(三) 机器学习中的小机灵





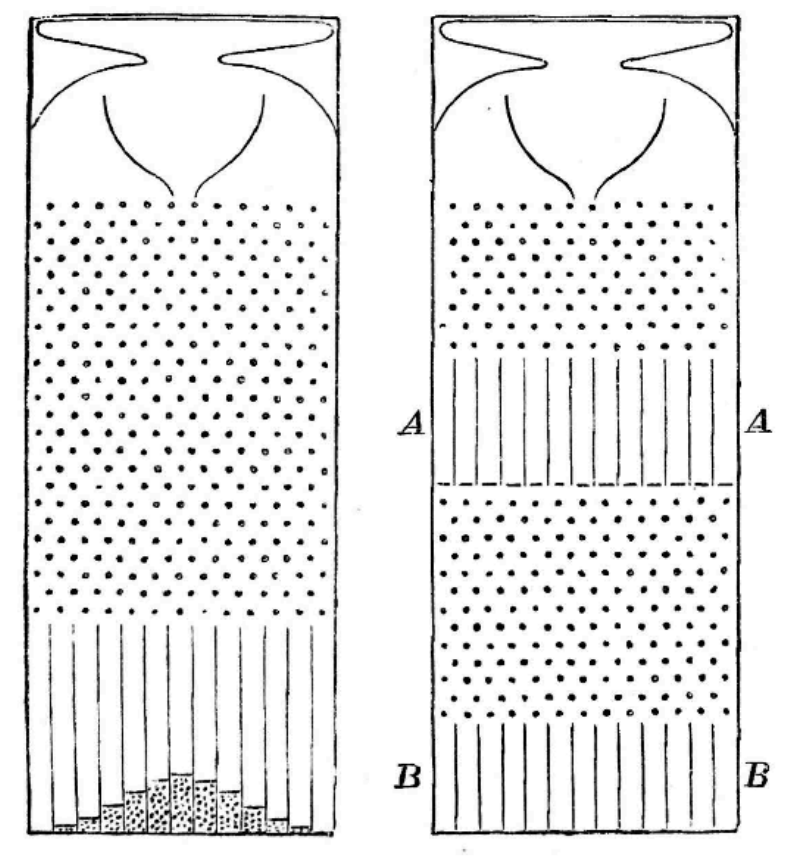
(四) 辛普森悖论


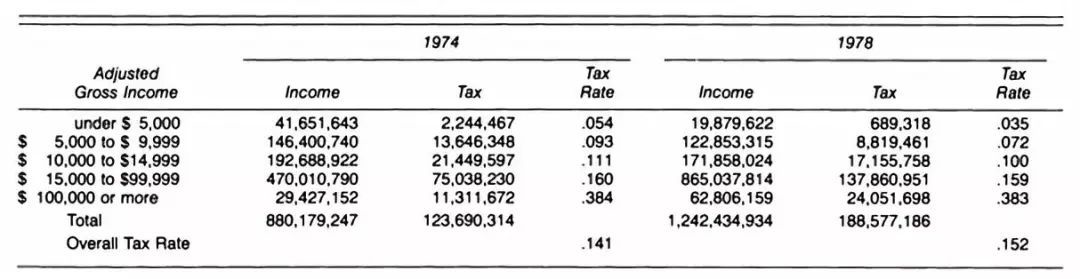
(五) 酸橙和柠檬



评论
