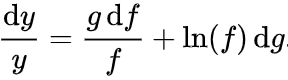本文约2400字,建议阅读7分钟
有兴趣挑战一下清朝的文言文版本的微积分教材吗?
[ 导读 ]你有见过160多年前清朝数学家写的微积分书吗?这可能是最难懂的高数教材了,堪称天书!近日,网上流传着一本清朝的微积分课本,其中的所有数学表达式都是用文言文书写的。小编不才,斗胆翻译了一下,看看这天书里面到底写了些什么。
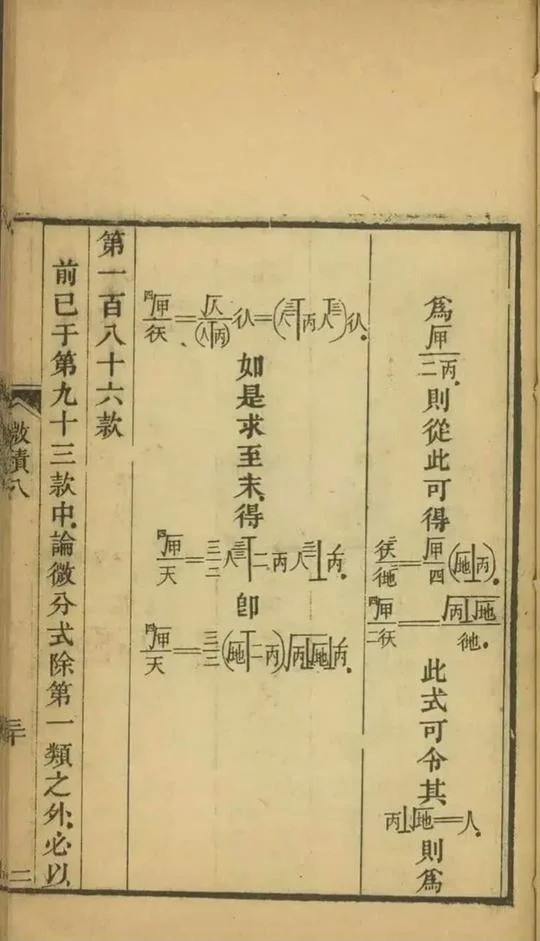
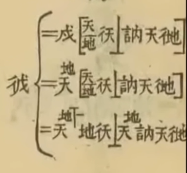
看到这些密密麻麻的数学式子,有唤起那种被高等数学微积分支配的恐惧了吗?其实,微积分不仅「折磨」着一代又一代大一刚开学的新同学们,早在清朝的时候,就已经开始折磨人了!是的,清朝的数学家李善兰将国外的微积分课本直接翻译成了文言文,供人们参考学习。快看看,什么叫文言文+微积分的双重酸爽。这酸爽,才够味!(战术后仰)首先,你可以用文言文的知识去读一下,看看能看懂多少。这里面怎么还有像是自己造的字呢?比如双人旁一个天,是什么鬼东西?
- 「分数」的「分子」是分母,「分母」是分子 。也就是说,如果看到「分数」,则它的倒数就是现代意义下的分数;
- 彳= d, 天 = x, 戍 = y,那么彳天 = dx, 彳戍 = dy;
所以,「戍=天^天」这句话的意思就是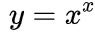 。这里,
。这里,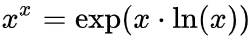 。而
。而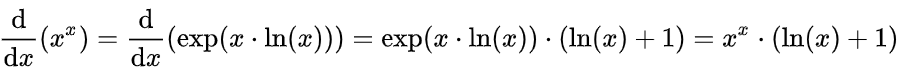 因此,
因此,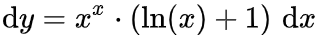 。而「彳戍=天^天(一丄訥天)彳天」就是 「dy = x^x (1+lnx) dx」,确实可以由上面那个式子整理得到。首先,先要明确
。而「彳戍=天^天(一丄訥天)彳天」就是 「dy = x^x (1+lnx) dx」,确实可以由上面那个式子整理得到。首先,先要明确 这个概念是什么。天和地在这里就不能理解为简单的x和y了,而是应该理解为f(x)与g(x)两个关于x的函数。换句话说,就是对
这个概念是什么。天和地在这里就不能理解为简单的x和y了,而是应该理解为f(x)与g(x)两个关于x的函数。换句话说,就是对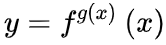 求导。首先将
求导。首先将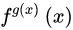 改写为:
改写为: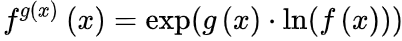 。将
。将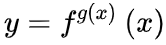 代入式子,将dx换到右边:dx可以与
代入式子,将dx换到右边:dx可以与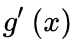 、
、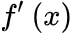 合并变成dg和df,所以:将
合并变成dg和df,所以:将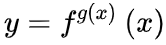 除到左边:
除到左边: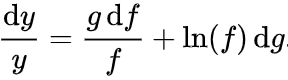 根据「分子」是分母,「分母」是分子、戍 = y、天= f(x)、地= g(x)的原则,就会发现,这样第一页就完全破译了,至于后面的几页就交给爱钻研的勇士们,小编的脑细胞已经阵亡了。。。
根据「分子」是分母,「分母」是分子、戍 = y、天= f(x)、地= g(x)的原则,就会发现,这样第一页就完全破译了,至于后面的几页就交给爱钻研的勇士们,小编的脑细胞已经阵亡了。。。
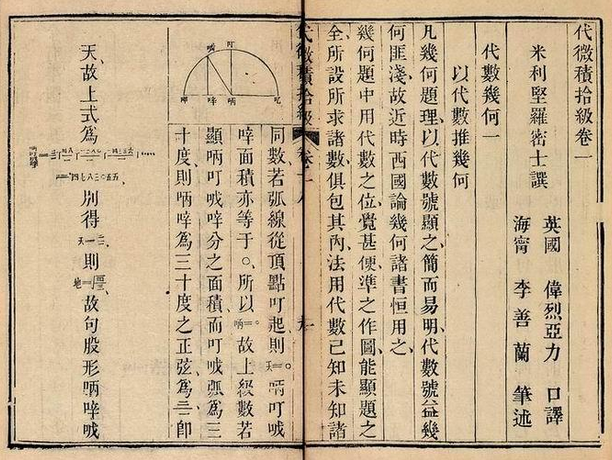
李善兰(1810年-1882年),字壬叔,号秋纫,清朝数学家。浙江省杭州府海宁县人。为清代数学史上的杰出代表,中国近代数学的先驱。李善兰于清嘉庆十五年(1810年)1月2日生于浙江海宁县硖石镇。10岁即通《九章算术》,15岁通习《几何原本》六卷,17岁参加杭州乡试未中。从此钻研天文、历算,成为远近闻名的数学家。1852年-1866年李善兰受聘于墨海书馆任编译。同治二年(1863年)被招至曾国藩幕中。同治五年(1866年)曾国藩出资三百金为李善兰刻《几何原本》后九卷。1868年,李善兰入同文馆总教习,执教算法,前后八年。同治十三年(1874年)升户部主事。光绪二年(1876年)升员外郎。光绪八年(1882年)升郎中。李善兰在1859年与英国传教士Alexander Wylie合作,翻译了Elias Loomis的「Elements of Analytical Geometry and of the Differential and Integral Calculus」(1850)。英文原著到1859年为止,已经出版到第10版,足以见得它相当受到大学教师的青睐。作者,Elias Loomis为LL. D(法学博士),在出版这一本教科书时,正担任纽约市立大学的数学与自然哲学教授 (Professor of Mathematics and Natural Philosophy, the University of the City of New York)。Loomis表示,本书「并非为了数学家、也不是为了那些拥有特殊天分或是数学的爱好者,而是为广大中等资质的大学生而写。」这或许也是英文原版畅销的原因之一吧。本书的中文译名为「代微积拾级」,强调本书依序讲述「代(数)」(解析几何)、「微(分)」与「积(分)」,「拾级」而上。「微分积分,为中土算书所未有,然观当代天算家,如董方立氏、项梅侣氏、徐君青氏、戴鄂士氏、顾尚之氏,暨李君秋纫,所著各书,其理有什近微分者,因不用代数式,或言之甚繁推之甚难,今特偕李君译此书,为微分积分入门之助。」
上引文提及之天算家依序为董佑城、项名达、徐有壬、戴煦、顾观光以及李善兰,都是十九世纪中国清代数学名家。不过,由于「不用代数式」,所以文章显得「言之甚繁,推之甚难」。在本书中,英文原文中的 analytical geometry(解析几何)一概翻译为「代数几何」。其中,Loomis主要运用微分系数(differential coefficient)来表示我们今日所谓的导数(derivative)。「函数与变数之比例,俱谓之微分,用ㄔ号记之。如戌 = 天三,则得比例ㄔ天 : ㄔ戌 :: 一 : 三天二。ㄔ天、ㄔ戌为天与戊之微分。后皆仿此。用表天与戌之变比例,以一、四两率相乘,二、三两率相乘则得ㄔ戌 = 三天二ㄔ天,此显函数戌之变比例,等于三天乘变数天之变比例,以ㄔ天约之得ㄔ天/ㄔ戌 = 三天二。此显变数之变比例约函数之变比例,等于函数之微系数也。」
「ㄔ天 : ㄔ戌 :: 一 : 三天二」也就是「dx:du=1:3×2」。由于分子、分母的位置,是反着的,于是,du/dx对应为ㄔ天/ㄔ戌。根据上述引文,针对任何一个函数 y=f(x) 而言,先求出 dy=f(x)dx,然后再得到 dy/dx=f(x)。如此,就可以避开导数定义中,[f(x+h)−f(x)]/h分子与分母同时趋近于零的难题。在Karl Weierstrass的分析算术化(arithmetization of analysis)提出的极限ε−δ定义之前,是无法解决的。此外,本书还有一个特点:相对于七卷的微分内容,积分只有两卷!
「积分为微分之还原,其法之要在识别微分所由生之函数,如已得天二之微分为二天ㄔ天,则有二天ㄔ天即知所由生之函数为天二,而天二即为积分。已得微分所由生之函数为积分,而积分或有常数附之,或无常数附之,既不能定,故式中恒附以常数,命为口丙,口丙或有同数或为0,须考题乃知。来本之视微分若函数诸小较之一,诸小较并之,即成函数,故微分之左系一禾字,指欲取诸微分之积分也。如下式禾二天ㄔ天=天+口丙。来氏说,今西国天算家大率不用,而惟用此禾字取其一览了然也。」
在上述引文中,李善兰将积分∫则译为「禾」。此外,Loomis未曾独立地定义定积分(definite integral),而是通过不定积分(indefinite integral)来定义,省去了定义定积分的麻烦。
https://www.bilibili.com/video/BV1RR4y1t7AH?from=search&seid=8170464341069800644&spm_id_from=333.337.0.0https://www.reddit.com/r/China_irl/comments/r0xh97/清朝微积分课本/https://highscope.ch.ntu.edu.tw/wordpress/?p=25200「zdr0」https://zhuanlan.zhihu.com/p/437864462




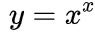 。
。
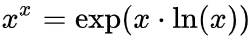 。
。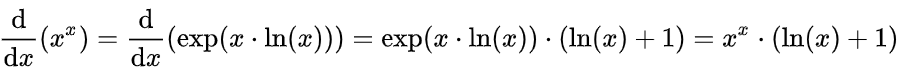
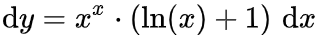 。
。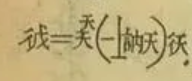

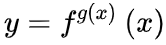 求导。
求导。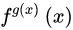 改写为:
改写为: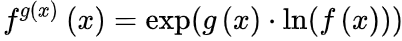 。
。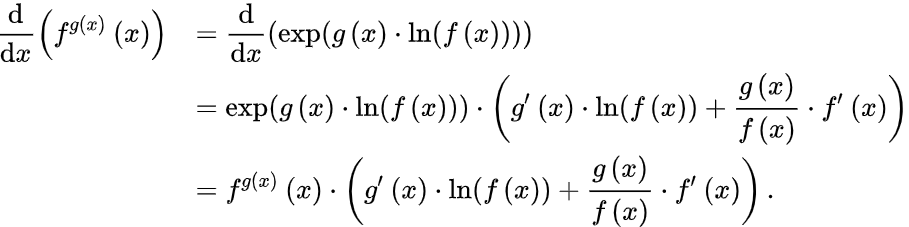
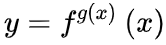 代入式子,将dx换到右边:
代入式子,将dx换到右边: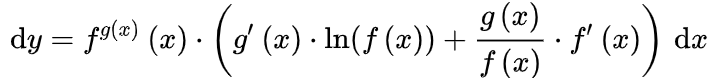
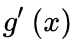 、
、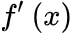 合并变成dg和df,所以:
合并变成dg和df,所以: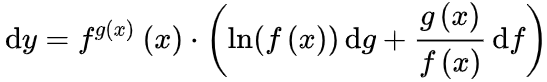
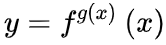 除到左边:
除到左边: