风控ML[13] | 特征稳定性指标PSI的原理与代码分享

PSI这个指标我们在风控建模前后都是需要密切关注的,这个指标直接反映了模型的稳定性,对于我们评估模型是否需要迭代有着直接的参考意义。今天我将从下面几方面来介绍一下这个指标。
Index
01 PSI的概念
02 PSI的生成逻辑
03 PSI的业务应用
04 PSI的Python实现
01 PSI的概念
PSI全称叫做“Population Stability Index”,中文翻译是群体稳定性指标,从风控应用的角度理解就是分组的测试与跨时间稳定性指标。
在我们建模的时候,数据(变量或者模型分)的分组占比分布是我们的期望值,也就是我们希望在测试数据集里以及未来的数据集里,也能够展示出相似的分组分布,我们称之为稳定。
PSI值没有指定的值域,我们需要知道的是值越小越稳定,一般在风控中会拿0.25来作为筛选阈值,即PSI>0.25我们就认定这个变量或者模型不稳定了。好了,那具体PSI怎么计算呢?不急,请接着看下一节。
02 PSI的生成逻辑
按照惯例,我们先把PSI的计算公式放上来:
其中,代表第i组的实际占比(占全部数量),代表第i组的期望占比(也就是训练时或者上线时的分组占比)。我们还是拿之前的《风控ML[5] | WOE前的分箱一定要单调吗》 文章里的数据来举例,具体可以看下面的表: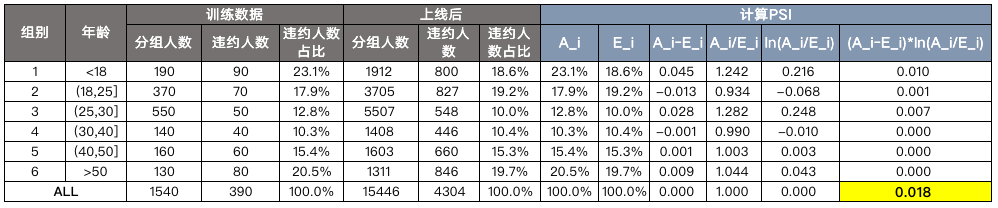
公式比较简单,在Excel里就可以实现了,结果计算出来PSI为0.018,所以是稳定的。
03 PSI的业务应用
那么有了这个稳定性指标,在具体的风控场景中可以怎么应用呢?我一般会在下面几个场景应用:
1、建模前筛选变量
2、模型上线后监控模型
建模前筛选变量
我们在做评分卡的时候一般都是会选择稳定性比较强的变量,因为模型一般上线后,下一次迭代都要1年后了,所以我们倾向于稳定性强的变量。那一般怎么筛选呢?我们从下面几个步骤来操作:
1)选择训练数据,并且确定变量的最优分箱(具体可以参考上篇关于最优分箱的文章)
[1] 风控建模中的自动分箱的方法有哪些
[2] 3种连续变量分箱方法的代码分享
2)初始化变量的期望占比分布
3)计算变量每个月的变量PSI
4)观察是否有PSI超过0.25的变量,剔除。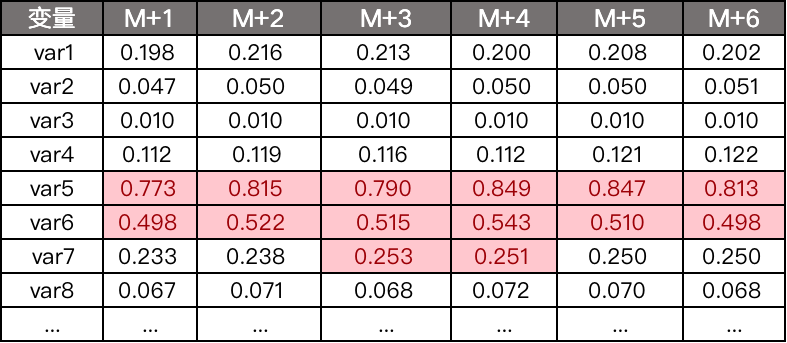
模型上线后监控模型
而模型上线后,我们一般会对模型分进行分组,比如A - F,所以我们会去监控模型分的分组稳定性,同样地,模型的入参也一样会监控。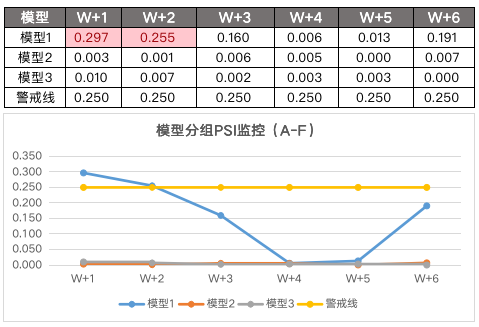
04 PSI的Python实现
我们在前一篇文章(3种连续变量分箱方法的代码分享 )里介绍的自动分箱算法的基础上,基于numpy进行PSI的计算,测试集可以在公众号SamShare的后台输入关键词cut获取。
import pandas as pd
import numpy as np
import random
import math
from scipy.stats import chi2
import scipy
# 测试数据构造,其中target为Y,1代表坏人,0代表好人。
df = pd.read_csv('./data/autocut_testdata.csv')
print(len(df))
print(df.target.value_counts()/len(df))
print(df.head())
def get_maxks_split_point(data, var, target, min_sample=0.05):
""" 计算KS值
Args:
data: DataFrame,待计算卡方分箱最优切分点列表的数据集
var: 待计算的连续型变量名称
target: 待计算的目标列Y的名称
min_sample: int,分箱的最小数据样本,也就是数据量至少达到多少才需要去分箱,一般作用在开头或者结尾处的分箱点
Returns:
ks_v: KS值,float
BestSplit_Point: 返回本次迭代的最优划分点,float
BestSplit_Position: 返回最优划分点的位置,最左边为0,最右边为1,float
"""
if len(data) < min_sample:
ks_v, BestSplit_Point, BestSplit_Position = 0, -9999, 0.0
else:
freq_df = pd.crosstab(index=data[var], columns=data[target])
freq_array = freq_df.values
if freq_array.shape[1] == 1: # 如果某一组只有一个枚举值,如0或1,则数组形状会有问题,跳出本次计算
# tt = np.zeros(freq_array.shape).T
# freq_array = np.insert(freq_array, 0, values=tt, axis=1)
ks_v, BestSplit_Point, BestSplit_Position = 0, -99999, 0.0
else:
bincut = freq_df.index.values
tmp = freq_array.cumsum(axis=0)/(np.ones(freq_array.shape) * freq_array.sum(axis=0).T)
tmp_abs = abs(tmp.T[0] - tmp.T[1])
ks_v = tmp_abs.max()
BestSplit_Point = bincut[tmp_abs.tolist().index(ks_v)]
BestSplit_Position = tmp_abs.tolist().index(ks_v)/max(len(bincut) - 1, 1)
return ks_v, BestSplit_Point, BestSplit_Position
def get_bestks_bincut(data, var, target, leaf_stop_percent=0.05):
""" 计算最优分箱切分点
Args:
data: DataFrame,拟操作的数据集
var: String,拟分箱的连续型变量名称
target: String,Y列名称
leaf_stop_percent: 叶子节点占比,作为停止条件,默认5%
Returns:
best_bincut: 最优的切分点列表,List
"""
min_sample = len(data) * leaf_stop_percent
best_bincut = []
def cutting_data(data, var, target, min_sample, best_bincut):
ks, split_point, position = get_maxks_split_point(data, var, target, min_sample)
if split_point != -99999:
best_bincut.append(split_point)
# 根据最优切分点切分数据集,并对切分后的数据集递归计算切分点,直到满足停止条件
# print("本次分箱的值域范围为{0} ~ {1}".format(data[var].min(), data[var].max()))
left = data[data[var] < split_point]
right = data[data[var] > split_point]
# 当切分后的数据集仍大于最小数据样本要求,则继续切分
if len(left) >= min_sample and position not in [0.0, 1.0]:
cutting_data(left, var, target, min_sample, best_bincut)
else:
pass
if len(right) >= min_sample and position not in [0.0, 1.0]:
cutting_data(right, var, target, min_sample, best_bincut)
else:
pass
return best_bincut
best_bincut = cutting_data(data, var, target, min_sample, best_bincut)
# 把切分点补上头尾
best_bincut.append(data[var].min())
best_bincut.append(data[var].max())
best_bincut_set = set(best_bincut)
best_bincut = list(best_bincut_set)
best_bincut.remove(data[var].min())
best_bincut.append(data[var].min()-1)
# 排序切分点
best_bincut.sort()
return best_bincut
age_bins=get_bestks_bincut(df, 'age', 'target')
df['age_bins'] = pd.cut(df['age'], bins=age_bins)
print("age的最优分箱切分点:", age_bins)
print("age的最优分箱结果:\n", df['age_bins'].value_counts())
df.head()

接下来导入测试集,计算PSI。
# 导入测试数据集
df_test = pd.read_csv('./data/psi_testdata.csv')
def cal_psi(df_train, df_test, var, target):
train_bins = get_bestks_bincut(df_train, var, target)
train_cut_nums = pd.cut(df_train[var], bins=train_bins).value_counts().sort_index().values
# 根据训练集分箱切分点对测试集进行切分
def cut_test_data(data, var, bincut):
# 扩大两端边界线
if bincut[0] > data[var].min()-1:
bincut.remove(bincut[0])
bincut.append(data[var].min()-1)
if bincut[-1] < data[var].max():
bincut.remove(bincut[-1])
bincut.append(data[var].max())
# 排序切分点
bincut.sort()
return bincut
test_cut_nums = pd.cut(df_test[var],
bins=cut_test_data(df_test, var, train_bins)).value_counts().sort_index().values
tt = pd.DataFrame(np.vstack((train_cut_nums, test_cut_nums)).T, columns=['train', 'test'])
# 计算PSI
E = tt['train'].values/tt['train'].values.sum(axis=0)
A = tt['test'].values/tt['test'].values.sum(axis=0)
A_sub_E = A-E
A_divide_E = A/E
ln_A_divide_E = np.log(A_divide_E) # numpy里的log其实指的是ln
PSI_i = A_sub_E * ln_A_divide_E
psi = PSI_i.sum()
return tt, psi
tt, psi = cal_psi(df, df_test, 'age', 'target')
print("PSI: ", psi)
tt

Reference
[1] 风控模型—群体稳定性指标(PSI)深入理解应用
https://zhuanlan.zhihu.com/p/79682292
