牛顿没能带红的货被高斯带红了-技术圈

第一篇

二、最小二乘法带红高斯消元法

1859 年，中国清代数学家李善兰翻译外国数学著作《代数学》（Elements of Algebra）时，将 Equation（指含有未知数的等式）一词译为方程，而将多个方程的组合称为方程组，沿用至今。而方程一词就是取自《九章算术》，原意应该是: 方，系数阵列；程，消元计量。

这里补上前一篇中提及的我国古代消元法的贡献，

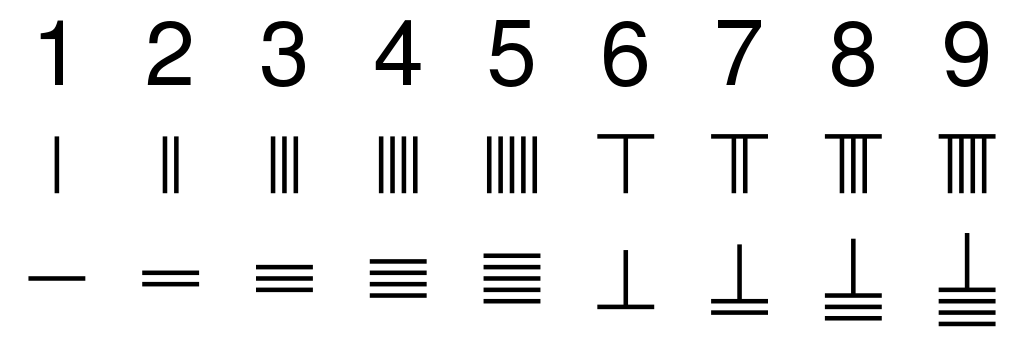
提出方程组，量化表示多个未知数之间的一组线性关系
提出消元法，解出隐含在方程组中的多个未知数
分离未知数和系数，通过处理系数阵列解出未知数

复习更多细节，请点击这里。一句话总结方程组和消元法这事的主要意义: 提出一个数学模型，用于量化表示多个未知数之间的线性关系，并为由已知关系求出未知数给出一种解决方案。

可惜的是，在当时的社会背景下很难找到这个数学模型的实际用武之地，更多的是理论价值。书中提出的很多类似程禾的方程问题反映了一种可建模的计算思维，但并不是实际生产中迫切需要的计算问题。

从现在的角度看，求解线性方程组的消元法貌似也不是什么神技，但是在一个还没有符号、没有计算工具甚至这方面计算需求的时代，能提出问题以及解法，算得上一项了不起的创举。

爱因斯坦曾说: 提出一个问题往往比解决一个问题更为重要，因为解决一个问题也许只是一个数学上或实验上的技巧问题。而提出新的问题、新的可能性，从新的角度看旧问题，却需要创造性的想像力，而且标志着科学的真正进步。

而我国古代消元法即提出了问题，又给出具体模型以及求解方法。只是，太超越时代了，没能找到发光的机会。

1牛顿也带不红

线性方程组的消元法并不是高斯（Gauss）首创，不管他知不知情古代中国的九章算术，即使在欧洲，一百多年前的艾萨克·牛顿（Isaac Newton）早在 1670 年提出了消元法。

牛大神认为他所知道的代数书里没有解联立方程的内容，因此他填补了这个空白。不过牛顿可能觉得这个神技暂时还派不上大用场，所以没有专门发表，而是剑桥大学于 1707 年和 1720 年分别以拉丁文和英文发表。

And you are to know, that by each Æquation one unknown Quantity may be taken away, and consequently, when there are as many Æquations and unknown Quantities, all at length may be reduc’d into one, in which there shall be only one Quantity unknown. — Newton [1720, pp. 60–61]

牛顿的影响力不言而喻，但他这个方法似乎并没有引起大家的关注。一个原因可能是当年没有互联网，要不然发个推特抖音啥的，即使没有引起热搜，也该会有一大波粉丝关注转发啊？不会惨得连个点赞都没有。

不过话说回来，牛顿那怼天怼地的爆脾气，要是生在如今，在互联网上估计是个大喷子。这里可以参考以牛顿为首的英国与整个欧洲大陆之间的学术恩怨。

有牛顿这一出戏就不难理解我国古代的消元法为什么没有引发大理论，太特么超越时代了，属于典型的奇技淫巧。

国外有些学者认为古代的经济只需要算术就足够了，九章算术第八章中的那些方程组问题是为训练算术技能而精心设计的练习题。

不过话说回来，数学理论的发现/发明和实用性之间存在时间间隔，这并不是偶然事件。

总之，用一句诗了结九章大法吧。

事了拂衣去，深藏身与名。

现在回到主题，就是消元法为何最终会被高斯拿去冠名呢。

2最小二乘法简史

最小二乘法是用某些类型的曲线和曲面去拟合数据的一类方法的基础。而拟合曲线和曲面的问题，在当前这届人类身上或许有几千年的历史了。这类问题的例子包括确定地球、天体的形状和大小以及它们的轨迹等。而现如今，最小二乘法的应用更广泛了，比如大家熟知的深度神经网络。

真正让最小二乘法发展起来的是近代天文学和大地测量学这两个领域，因为时代召唤科学家和数学家寻求解决办法以应对在探索时代导航地球海洋的挑战。例如，准确描述天体的行为是使船只能够在公海航行的关键，因为在这种情况下，水手不再能够依靠陆地目击者进行航行了。

一个在天，一个在地，所谓天时地利，就看哪个人才有幸成为网红了。

具体来说，最小二乘法的起源在于一个科学问题，该问题在 18 世纪尚未完全解决: 如何根据测量数据做出准确的预测。在 18 世纪中叶，天文观测与源自牛顿理论的轨道公式之间的差异甚至让人们对引力的平方反比产生了怀疑。欧拉（Euler）和拉普拉斯（Laplace）都推测引力定律可能需要修改。

另外，欧拉并不信任方程的组合，并认为误差实际上会累积，而不是统计学家认为的随机误差往往会相互抵消。德国天文学家托比亚斯·梅耶（Tobias Mayer）应用拟合方法和观测数据成功预测月球轨道。特别是拉普拉斯，他推导出了拟合轨道，证明了牛顿的正确性。

而另一个关于星空的大事件直接将人和技推上了历史舞台。那就是高斯在 1801 年成功预测出矮行星谷神星的轨道而成为一代大网红。

.谷神星.

我们来回顾一下高斯通过计算找出谷神星的历史故事。高斯那时代老早知道行星的运行轨道是一个椭圆，它可以用如下方程表示:

f(x,y)=a x^{2}+2 b x y+c y^{2}+2 d x+2 e y+1=0

然后拿到一组观测数据进行拟合即可，但实际情况并非这么简单。因为行星、地球都是围绕太阳在转动，而我们得到的是从地球上观测到的小行星在天空的角度。可想而知，那个轨迹是非常复杂的。那么如何确定它的轨道参数，并能预测它的走向呢？

首先让我大概了解一下行星轨道可以由哪些参数确定，

行星轨道平面相对于黄道平面的两个角度。
行星轨道的大小和偏心率，即长短轴的长度。
轨道主轴相对于地球轨道的倾斜度。

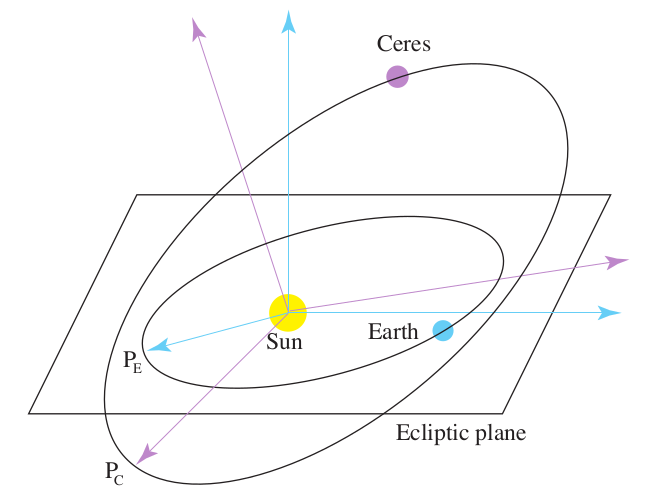
高斯使用皮亚齐（Piazzi）提供的 22 组观测数据来预测谷神星的走向。

y_{\mathrm{obs}}=\left[\begin{array}{c} R_{1},D_{1},R_{2},D_{2},\dots,R_{22},D_{22} \end{array}\right]^{\top}

这些观测数据包括一个特定的时间点以及两个角度，即赤经和赤纬，表示在天球坐标系中的方向。

现在要用这些观测数据计算出谷神星的轨道模型，其中表示待定的轨道参数向量，具体模型涉及大量天体动力学，就不管它了。我们只要知道这几个参数一旦确定下来就可以计算出来谷神星在天球的方向。当然这里假设不受其他较大天体的影响，比如木星。

然后定义代价函数为:

J(\theta)=\displaystyle \frac{\epsilon^{T} W^{-1} \epsilon}{2}

其中，，为参数残差向量，权值。这里，高斯使用了拉格朗日（Lagrange）提出的二次型来表示加权误差。

这特么的用现在的话说就是，给神经网络配个损失函数。

最后，转为如下优化问题，

\quad \hat{\theta}=\underset{\theta}{\operatorname{argmin}} J(\theta)

高斯预测谷神星轨道的策略大致如下，

选择三个观测值：1 月 1 日，1 月 21 日和 2 月 11 日。
计算与观测值匹配的标称轨道。

计算非线性微分方程的泰勒级数逼近。
迭代式提升标称轨道的精度。

调整轨道的线性逼近版本，以使最小化所有 22 个观测值的误差平方和。

高斯最初仅使用了 22 项观测值中的 3 项，根据空间位置计算出轨道参数的近似值。然后，通过使用这种近似的轨道计算，他可以修改距离的初始计算以获得更精确的轨道，以便拟合所有观察结果。

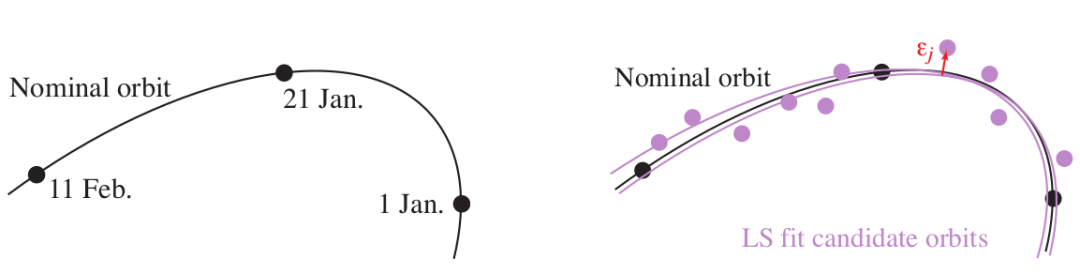
那么，谷神星的轨道到底是怎么被计算出来的？所谓有公式才有真相。

一句话总结: 首先将误差函数线性化，接着使用极大似然估计导出最小二乘法，推出法方程并用消元法求解，更新参数，下一轮迭代。

好吧，小爱同学，听说你数学不大好，我还是用你看得懂的符号吧。

令初始标称轨道参数为，在其附近线性表示为，

\Phi(\theta) \approx \Phi\left(\theta_{0}\right)+\Phi_{\theta_{0}}\left(\theta-\theta_{0}\right),

令以及。

J_{\text {linear }}(\theta)=\frac{\left(\delta y-\Phi_{\theta_{0}} \delta \theta\right)^{T} W^{-1}\left(\delta y-\Phi_{\theta_{0}} \delta \theta\right)}{2}

求的梯度，

\frac{\partial J_{\text {linear }}(\theta)}{\partial \theta}=-\Phi_{\theta_{0}}^{T} W^{-1}\left(\delta y-\Phi_{\theta_{0}} \delta \theta\right)

其值设为 0 得法方程，

\Phi_{\theta_{0}}^{T} W^{-1} \Phi_{\theta_{0}} \delta \theta=\Phi_{\theta_{0}}^{T} W^{-1} \delta y.

该问题中，方程数量比未知数个数显然要多，因此通过所谓的最小二乘法最小化一个误差平方的加权和。迭代中求解法方程得得，然后更新参数。

当然，高斯那会儿还没有矩阵，处理线性方程组还是以系数散兵形式，因此涉及一大堆系数的操作运算。为了导出法方程，高斯使用了自己的符号，类似下面这样子，

[x y]=x y+x^{\prime} y^{\prime}+x^{\prime \prime} y^{\prime \prime}+\ldots,

\begin{array}{l} {[x y, 1]=[x y]-\displaystyle \frac{[a x][a y]}{[a a]}}, \\ {[x y, 2]=[x y, 1]-\displaystyle \frac{[b x, 1][b y, 1]}{[b b, 1]}}, \end{array}

\begin{array}{l} &A=[a n] \quad+[a a] p \quad+[a b] q \quad+[a c] r+\ldots \\ &B=[b n, 1] \quad\quad\quad\quad\!\!\!+[b b, 1] q+\;[b c,1]r+\ldots \\ &C=[c n, 2] \qquad\qquad\qquad\quad\quad\!+[c c, 2] r+\ldots \\ &\quad etc. \end{array}

现代人看着头大，显然不如上面用矩阵语言表达来的简炼。

好了，期间高斯搞了个骚操作，认为只有当测量误差分布为正态分布时才能符合千百年来大家都在用的平均法则，因此能够合理地用上所谓的最小二乘法，而为了求解它导出了一个线性方程组，即法方程。因此，自然而然地引出了如何计算线性方程组的问题，即所谓的高斯消元法。

其实，既然有最小二乘法，那是不是也可以有最小一乘法啊？是的，这个需要另外开一篇。

勒让德（Legendre）和高斯分别在 1805 年和 1809 年发表了勒让德所称的最小二乘法时，这是一种通过最小化误差平方之和来对超定联立线性方程组中的未知数作统计推断的一种方法。人类对未知数的追求终于有了大法宝，从而逐渐引发了解决联立线性方程组的社会需求。

虽然勒让德先发表最小二乘法，但是高斯凭借成功预测谷神星一炮走红，成为带货力量全球第一的大网红。

谷神星事件的最大赢家非高斯莫属，即赢得了声望，又获得了最小二乘法、高斯分布以及高斯消元法三大发明/冠名权，活脱脱人生大赢家。

3高斯消元法

对了，本文男一号好像是高斯消元法，但貌似被男二号抢了戏。现在有个关于个未知量的等式构成的线性方程组，

\begin{array}{c} a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1n} x_{n}&= b_{1} \\ a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2n} x_{n}&= b_{2} \\ a_{m 1} x_{1}+a_{m 2} x_{2}+\cdots+a_{mn} x_{n}&= b_{m} \end{array}

要计算一个通用解，其中是未知量，而和是已知常数。称为方程组的系数，而的集合称为方程组的右侧。对形如上面这样的线性系统，它的解存在三种可能，

唯一解决方案: 的值有且只有一组同时满足所有方程。
无解: 没有一组的值同时满足所有方程，即解集为空。
无限多个解: 有无数组的值，可同时满足所有方程。

不难证明，如果一个方程组具有多个解，那么它肯定有无穷个解。

拿到一个线性方程组，一部分工作是确定它是属于这三种可能性中的哪一种，另一部分工作是计算解（如果唯一）或者描述所有解的集合（如果存在许多解）。

高斯消元法恰恰是可实现所有这些目标的工具。高斯消元通过有规律的操作从相关方程中依次消除未知量并最终形成一个易于求解的线性方程组。

消元过程依赖于三个简单的操作，通过这些操作可以将一个系统转换为另一个等解系统。为了描述这些操作，让表示第个方程

E_{k}: \quad a_{k 1} x_{1}+a_{k 2} x_{2}+\cdots+a_{k n} x_{n}=b_{k}

线性方程组可写为，

\mathcal{S}=\left\{\begin{array}{c} E_{1} \\ E_{2} \\ \vdots \\ E_{m} \end{array}\right\}

对于线性系统，以下三个基本运算中的每一个都会得出等价系统（解相同）。

1、互换等个和第个方程。也就是说，如果

\mathcal{S}=\left\{\begin{array}{c} E_{1} \\ \vdots \\ E_{i} \\ \vdots \\ E_{j} \\ \vdots \\ E_{m} \end{array}\right\}, \quad \text {那么} \quad \mathcal{S}^{\prime}=\left\{\begin{array}{c} E_{1} \\ \vdots \\ E_{j} \\ \vdots \\ E_{i} \\ \vdots \\ E_{m} \end{array}\right\}

2、将第个方程乘以一个非 0 数。即，

\mathcal{S}^{\prime}=\left\{\begin{array}{c} E_{1} \\ \vdots \\ \alpha E_{i} \\ \vdots \\ E_{m} \end{array}\right\}, \quad \text {其中 } \alpha \neq 0

3、数乘第个方程并加到第个方程。即，

\mathcal{S}^{\prime}=\left\{\begin{array}{c} E_{1} \\ \vdots \\ E_{i} \\ \vdots \\ E_{j}+\alpha E_{i} \\ \vdots \\ E_{m} \end{array}\right\}

易知这些操作不改变方程组的解，证明从略。它的核心思想就是，将一个线性方程组可程序化地转换为另一个更简单但解相同的线性方程组。这点也是上篇中我国古代数学家提出的分禾消元法在思路上是一致的。

.方阵的消元法.

实际中处理的往往是针对个方程式和个未知数的问题，因此如果有解那必然是唯一解。

\begin{array}{c} a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n}=& b_{1} \\ a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2 n} x_{n}=& b_{2} \\ a_{n1} x_{1}+a_{n2} x_{2}+\cdots+a_{n n} x_{n}=& b_{n} \end{array}

右边那列一起考虑，其对应的增广系数阵列为以下形式，

\left[\begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1 n} & b_{1} \\ a_{21} & a_{22} & \cdots & a_{2 n} & b_{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{n n} & b_{n} \end{array}\right]

通过初等行变换，可以将上面阵列转换为如下形式，

\left[\begin{array}{cccc|c} t_{11} & t_{12} & \cdots & t_{1 n} & c_{1} \\ 0 & t_{22} & \cdots & t_{2 n} & c_{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & t_{n n} & c_{n} \end{array}\right]

这里假设每个。用这种方法将一个线性方程组三角化处理，然后通过反向代换即可求得唯一解。

.高斯–若尔当消元法.

除了原版高斯消元法，还有其他版本，其中高斯-若尔当消元法就是教材上常见的另一个版本，它与标准版的高斯消元法主要有两个区别，

将列主元转化为。
将消除列主元上方和下方的所有项。

因此最后的系数矩阵为单位矩阵.

此时，待求解的线性系统关联的增广系数阵列为，

\left[\begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1 n} & b_{1} \\ a_{21} & a_{22} & \cdots & a_{2 n} & b_{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} & b_{n} \end{array}\right]

使用初等行变换将该它简化为，

\left[\begin{array}{cccc|c} 1 & 0 & \cdots & 0 & s_{1} \\ 0 & 1 & \cdots & 0 & s_{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & s_{n} \end{array}\right]

显然，解出现在最后一列中（即），因此该过程不需要执行反向替换的步骤。

该消元法更接近于我国古代提出的分禾消元法，稍微不同的是古代版本没有单位化，最终得到的是一个对角矩阵。

为了将整个过程形象地展示出来，来一段视频。

我们知道，其实方程组中的每个方程对应一个平面，那么方程组如果有唯一解的话，上面例子中就是三个平面的交点。高斯-若尔当消元法的过程就相当于将各个平面转到与相应的坐标轴垂直，最终解就自然出来了。

.算法复杂度.

算法复杂度比较，只保留最高次，

高斯消元法，次乘除和加减。
高斯-若尔当消元法，次乘除和加减。

高斯-若尔当消元法比高斯消元法大约多了 50% 的计算量。那么自然有个问题，它存在的意义是什么呢？

尽管不建议将高斯-若尔当消元法用于实际求解线性方程组，但它在理论推导上确实具有很大用途。

由于最后得到的是一个单位矩阵，这点有什么用途呢？可以用来求逆矩阵，这也是引入高斯-若尔当消元法的主要原因。

另外，在计算机实际应用高斯消元法还需要另外一些改动以减少数值误差，此处略过。

4小结

前一篇里，我们回顾了古代消元法和克莱姆法则。看了这一篇发现消元法比克莱姆法则还来得更实用。

这里有个问题，在没有变元符号化的两千多年前，为什么我们能提出消元法？

消元法不需要显式定义符号，这或许是一个原因。分禾消元法中每一列对应一个未知量，这个量不需要参与运算，因此在两千多年前的中国在根本没有将变元符号化的情况下就提出了这个算法。但克莱姆法则的推导却需要有变元的参与，所以需要到近几百年才能推出。

整个过程不需要显式表示未知数。但是，仔细一想，这里要求的抽象化能力比后来欧洲有了符号化以后明显会更高一些。

而在高斯时代，一切都已经具备，只缺一个被带上热搜的热门事件。

总之，带货这件事，不是网红肯定很难，但即便是超级网红（如牛顿）带错时间也不行。

还是得看天时、地利、人和。而大网红高斯生得逢时，才华尽显。从谷神星轨道预测这个事件看，在一定程度上，高斯称得上是机器学习的鼻祖。

相关阅读

牛顿没能带红的货被高斯带红了

1牛顿也带不红