【数据竞赛】Kaggle实战之单类别变量特征工程总结!
特征工程--类别变量完结篇!

这是一个系列篇,后续我们会按照我们第一章中的框架进行更新,因为大家平时都较忙,不会定期更新,如有兴趣欢迎长期关注我们的公众号,如有任何建议可以在评论区留言,该系列以往的经典内容可参考下面的篇章。
1. kaggle竞赛宝典-竞赛框架篇!
4.1 kaggle竞赛宝典-样本筛选篇!
4.2 kaggle竞赛宝典-样本组织篇!



类别特征编码
在很多表格类的问题中,高基数的特征类别处理一直是一个困扰着很多人的问题,究竟哪一种操作是最好的,很难说,不同的数据集有不同的特性,可能某一种数据转化操作这A数据集上取得了提升,但在B数据集上就不行了,但是知道的技巧越多,我们能取得提升的概率往往也会越大。此处我们会介绍几种常见的处理类别特征的方法。
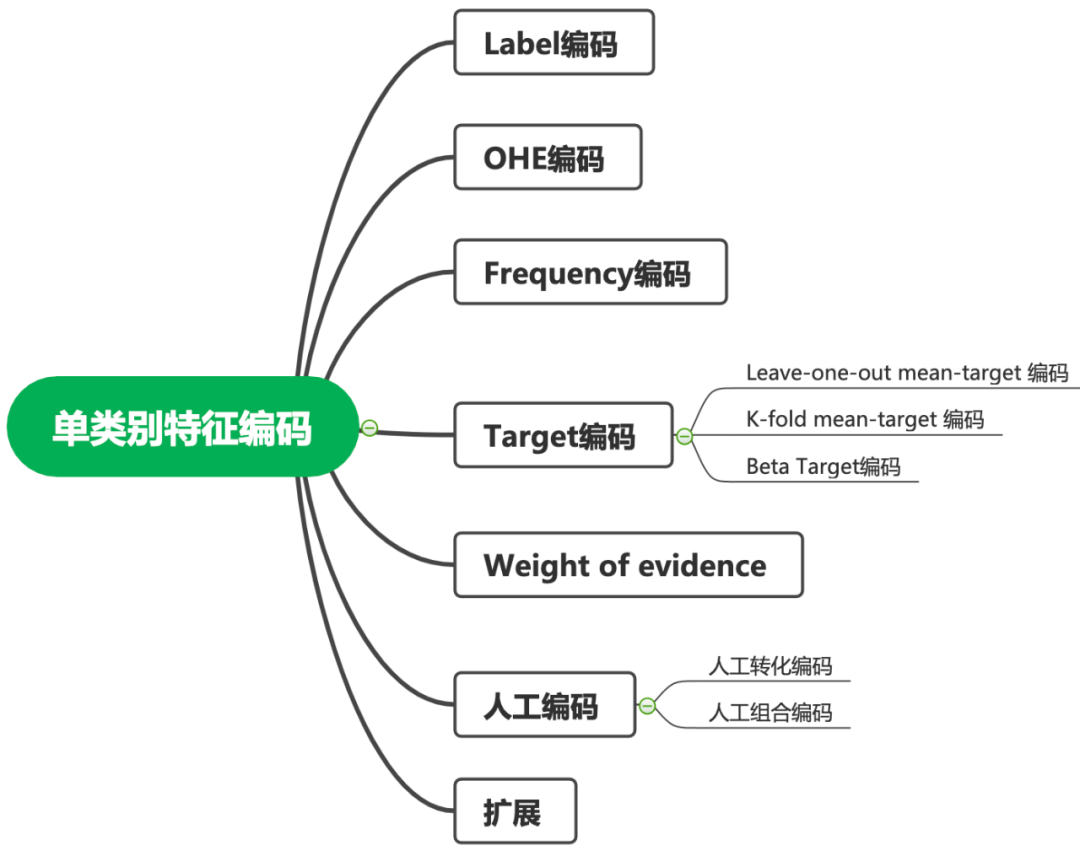
1. Label编码
无序的类别变量,在很多时候是以字符串形式的出现的,例如:
颜色:红色,绿色,黑色... 形状:三角形,正方形,圆形...
而我们知道,梯度提升树模型是无法对此类特征进行处理的。直接将其输入到模型就会报错。而这个时候最为常见的就是使用LabelEncoder对其进行编码。LabelEncoder可以将类型为object的变量转变为数值形式,具体的例子如下:

LabelEncoder默认会先将object类型的变量进行排序,然后按照大小顺序进行的编码,此处N为该特征中不同变量的个数。几乎所有的赛题中都会这么做,这样做我们就可以将转化后的特征输入到模型,虽然这并不是模型最喜欢的形式,但是至少也可以吸收10%左右的信息,会总直接丢弃该变量的信息好很多。
对应代码:
from sklearn import preprocessing
df = pd.DataFrame({'color':['red','blue','black','green']})
le = preprocessing.LabelEncoder()
le.fit(df['color'].values)
df['color_labelencode'] = le.transform(df['color'].values)
df
| color | color_labelencode | |
|---|---|---|
| 0 | red | 3 |
| 1 | blue | 1 |
| 2 | black | 0 |
| 3 | green | 2 |
2. One-Hot编码
One-Hot编码对于一个类别特征变量,我们对每个类别,使用二进制编码(0或1)创建一个新列(有时称为dummy变量),以表示特定行是否属于该类别。One-Hot编码可以将一个基数为的类别变量转变为个二元向量,我们以上面的颜色为案例,进行one-hot编码之后就得到:
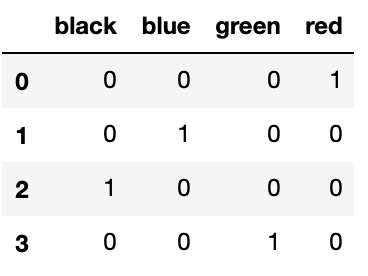
我们发现One-Hot编码将我们的数据展开之后内存的消耗变得非常大,因为使用One-Hot编码时需要创建额外的列,为我们需要编码的特征列中的每个每个唯一值创建一个列。也就是说,如果我们有一个包含10000个不同值的类别特征,那么在One-Hot编码之后将会生成10000个额外的新的列,这是不可以接受的。
但它的好处也非常明显,One-Hot编码之后,我们的线性模型可以更好的吸收High-Cadinality的类别信息,原先我们的采用线性模型,那么我们类别变量A的对预测带来的贡献为,, (A由(组成)我们发现类别2的贡献就是类别1的一倍,这很明显和我们的直觉不符,但是展开之后,我们类别变量A对预测带来的贡献为:。变量之间的关系变得更加合理了。所以One-Hot编码对于很多线性模型是有必要的。
那么对于XGBoost,LightGBM之类的树模型是否有必要呢?答案是有的!在我们的实践中,很多时候对高基数的类别特征直接进行One-Hot编码的效果往往可能不如直接LabelEncoder来的好。但是当我们的类别变量中有一些变量是人为构造的,加入了很多噪音,这个时候将其展开,那么模型可以更加快的找到那些非构建的类别。(参考讯飞18年举办的推荐比赛),取得更好的效果。
对应代码:
from sklearn import preprocessing
df = pd.DataFrame({'color':['red','blue','black','green']})
pd.get_dummies(df['color'].values)
| black | blue | green | red | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 |
3. Frequency编码
Frequency编码是数据竞赛中使用最为广泛的技术,在90%以上的数据建模的问题中都可以带来提升。因为在很多的时候,频率的信息与我们的目标变量往往存在有一定关联,例如:
在音乐推荐问题中,对于乐曲进行Frequency编码可以反映该乐曲的热度,而热度高的乐曲往往更受大家的欢迎; 在购物推荐问题中,对于商品进行Frequency编码可以反映该商品的热度,而热度高的商品大家也更乐于购买; 微软设备被攻击概率问题中,预测设备受攻击的概率,那么设备安装的软件是非常重要的信息,此时安装软件的count编码可以反映该软件的流行度,越流行的产品的受众越多,那么黑客往往会倾向对此类产品进行攻击,这样黑客往往可以获得更多的利益
Frequency编码通过计算特征变量中每个值的出现次数来表示该特征的信息,详细的案例如下所示:
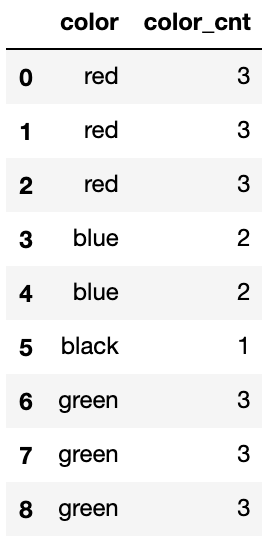
在很多实践问题中,Count编码往往可以给模型的效果带来不错的帮助。
对应代码:
from sklearn import preprocessing
df = pd.DataFrame({'color':['red','red','red','blue','blue','black','green','green','green']})
df['color_cnt'] = df['color'].map(df['color'].value_counts())
df
| color | color_cnt | |
|---|---|---|
| 0 | red | 3 |
| 1 | red | 3 |
| 2 | red | 3 |
| 3 | blue | 2 |
| 4 | blue | 2 |
| 5 | black | 1 |
| 6 | green | 3 |
| 7 | green | 3 |
| 8 | green | 3 |
4. target编码
target编码是06年提出的一种结合标签进行编码的技术,它将类别特征替换为从标签衍生而来的特征,在类别特征为高基数的时候非常有效。该技术在非常多的数据竞赛中都取得了非常好的效果,但特别需要注意过拟合的问题。在kaggle竞赛中成功的案例有owen zhang的leave-one-out的操作和莫斯科GM的基于K-fold的mean-target编码,此处我们介绍两种Mean-target编码;
4.1. Leave-one-out mean-target 编码
Leave-one-out mean-target编码的思路相对简单,我们每次编码时,不考虑当前样本的情况,用其它样本对应的标签的均值作为我们的编码,而测试集则用全部训练集样本的均值进行编码,案例如下:
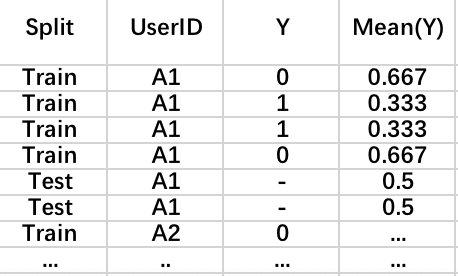
的案例摘自owen-zhang(曾经的kaggle第一名)的分享。
对应代码:
from sklearn import preprocessing
from pandas import pandas
from category_encoders.leave_one_out import LeaveOneOutEncoder
df_tr = pd.DataFrame({'color':['red','red','red','red','red','red','black','black'], 'label':[1,0,1,1,0,1,1,0]})
df_te = pd.DataFrame({'color':['red','red','black'] })
loo = LeaveOneOutEncoder()
loo.fit_transform(df_tr['color'], df_tr['label'])
| color | |
|---|---|
| 0 | 0.6 |
| 1 | 0.8 |
| 2 | 0.6 |
| 3 | 0.6 |
| 4 | 0.8 |
| 5 | 0.6 |
| 6 | 0.0 |
| 7 | 1.0 |
loo.transform(df_te['color'])
| color | |
|---|---|
| 0 | 0.666667 |
| 1 | 0.666667 |
| 2 | 0.500000 |
4.2. K-fold mean-target 编码
K-fold mean-target编码的基本思想来源于Mean target编码。K-fold mean-target编码的训练步骤如下,我们先将训练集划分为K折;
在对第A折的样本进行编码时,我们删除K折中A折,并用剩余的数据计算如下公式:
后利用上面计算得到的值对第A折进行编码; 依次对所有折进行编码即可。
首先我们先理解一下上面的公式,最原始的Mean-target编码是非常容易导致过拟合的,这其中过拟合的最大的原因之一在于对于一些特征列中出现次数很少的值过拟合了,比如某些值只有1个或者2到3个,但是这些样本对应的标签全部是1,怎么办,他们的编码值就应该是1,但是很明显这些值的统计意义不大,大家可以通过伯努利分布去计算概率来理解。而如果我们直接给他们编码了,就会误导模型的学习。那么我们该怎么办呢?
加正则!
于是我们就有了上面的计算式子,式子是值出现的次数,是它对应的概率,是全局的均值, 那么当为0同时比较小的时候, 就会有大概率出现过拟合的现象,此时我们调大就可以缓解这一点,所以很多时候都需要不断地去调整的值。
from category_encoders.target_encoder import TargetEncoder
from sklearn import base
from sklearn.model_selection import KFold
df = pd.DataFrame({'Feature':['A','B','B','B','B', 'A','B','A','A','B','A','A','B','A','A','B','B','B','A','A'],\
'Target':[1,0,0,1,1, 1,0,0,0,0,1, 0,1, 0,1,0,0,0,1,1]})
class KFoldTargetEncoderTrain(base.BaseEstimator, base.TransformerMixin):
def __init__(self, colnames,targetName,n_fold=5,verbosity=True,discardOriginal_col=False):
self.colnames = colnames
self.targetName = targetName
self.n_fold = n_fold
self.verbosity = verbosity
self.discardOriginal_col = discardOriginal_col
def fit(self, X, y=None):
return self
def transform(self,X):
assert(type(self.targetName) == str)
assert(type(self.colnames) == str)
assert(self.colnames in X.columns)
assert(self.targetName in X.columns)
mean_of_target = X[self.targetName].mean()
kf = KFold(n_splits = self.n_fold, shuffle = False, random_state=2019)
col_mean_name = self.colnames + '_' + 'Kfold_Target_Enc'
X[col_mean_name] = np.nan
for tr_ind, val_ind in kf.split(X):
X_tr, X_val = X.iloc[tr_ind], X.iloc[val_ind]
X.loc[X.index[val_ind], col_mean_name] = X_val[self.colnames].map(X_tr.groupby(self.colnames)[self.targetName].mean())
X[col_mean_name].fillna(mean_of_target, inplace = True)
if self.verbosity:
encoded_feature = X[col_mean_name].values
print('Correlation between the new feature, {} and, {} is {}.'.format(col_mean_name,
self.targetName,
np.corrcoef(X[self.targetName].values, encoded_feature)[0][1]))
if self.discardOriginal_col:
X = X.drop(self.targetName, axis=1)
return X
class KFoldTargetEncoderTest(base.BaseEstimator, base.TransformerMixin):
def __init__(self,train,colNames,encodedName):
self.train = train
self.colNames = colNames
self.encodedName = encodedName
def fit(self, X, y=None):
return self
def transform(self,X):
mean = self.train[[self.colNames,self.encodedName]].groupby(self.colNames).mean().reset_index()
dd = {}
for index, row in mean.iterrows():
dd[row[self.colNames]] = row[self.encodedName]
X[self.encodedName] = X[self.colNames]
X = X.replace({self.encodedName: dd})
return X
'''
训练集编码
'''
targetc = KFoldTargetEncoderTrain('Feature','Target',n_fold=5)
new_train = targetc.fit_transform(df)
new_train
Correlation between the new feature, Feature_Kfold_Target_Enc and, Target is 0.11082358287080162.
| Feature | Target | Feature_Kfold_Target_Enc | |
|---|---|---|---|
| 0 | A | 1 | 0.555556 |
| 1 | B | 0 | 0.285714 |
| 2 | B | 0 | 0.285714 |
| 3 | B | 1 | 0.285714 |
| 4 | B | 1 | 0.250000 |
| 5 | A | 1 | 0.625000 |
| 6 | B | 0 | 0.250000 |
| 7 | A | 0 | 0.625000 |
| 8 | A | 0 | 0.714286 |
| 9 | B | 0 | 0.333333 |
| 10 | A | 1 | 0.714286 |
| 11 | A | 0 | 0.714286 |
| 12 | B | 1 | 0.250000 |
| 13 | A | 0 | 0.625000 |
| 14 | A | 1 | 0.625000 |
| 15 | B | 0 | 0.250000 |
| 16 | B | 0 | 0.375000 |
| 17 | B | 0 | 0.375000 |
| 18 | A | 1 | 0.500000 |
| 19 | A | 1 | 0.500000 |
'''
测试集编码
'''
test_targetc = KFoldTargetEncoderTest(new_train,
'Feature',
'Feature_Kfold_Target_Enc')
new_test = test_targetc.fit_transform(test)
4.3. Beta Target编码
Beta Target编码来源于kaggle之前的竞赛Avito Demand Prediction Challenge第14名方案。该编码和传统Target Encoding不一样,
Beta Target Encoding可以提取更多的特征,不仅仅是均值,还可以是方差等等; 在开源中,是没有进行N Fold提取特征的,所以可能在时间上提取会更快一些;
Beta Target编码利用Beta分布作为共轭先验,对二元目标变量进行建模。Beta分布用和来参数化,和可以被当作是重复Binomial实验中的正例数和负例数。分布中许多有用的统计数据可以用和表示,例如,
平均值:
方差:
等等。
从实验对比上我们发现,使用Beta Target Encoding可以得到大幅提升。因为Beta Target Encoding属于类别编码的一种,所以适用于高基数类别特征的问题。
对应代码:
import numpy as np
import pandas as pd
from sklearn.preprocessing import LabelEncoder
'''
代码摘自原作者:https://www.kaggle.com/mmotoki/beta-target-encoding
'''
class BetaEncoder(object):
def __init__(self, group):
self.group = group
self.stats = None
# get counts from df
def fit(self, df, target_col):
# 先验均值
self.prior_mean = np.mean(df[target_col])
stats = df[[target_col, self.group]].groupby(self.group)
# count和sum
stats = stats.agg(['sum', 'count'])[target_col]
stats.rename(columns={'sum': 'n', 'count': 'N'}, inplace=True)
stats.reset_index(level=0, inplace=True)
self.stats = stats
# extract posterior statistics
def transform(self, df, stat_type, N_min=1):
df_stats = pd.merge(df[[self.group]], self.stats, how='left')
n = df_stats['n'].copy()
N = df_stats['N'].copy()
# fill in missing
nan_indexs = np.isnan(n)
n[nan_indexs] = self.prior_mean
N[nan_indexs] = 1.0
# prior parameters
N_prior = np.maximum(N_min-N, 0)
alpha_prior = self.prior_mean*N_prior
beta_prior = (1-self.prior_mean)*N_prior
# posterior parameters
alpha = alpha_prior + n
beta = beta_prior + N-n
# calculate statistics
if stat_type=='mean':
num = alpha
dem = alpha+beta
elif stat_type=='mode':
num = alpha-1
dem = alpha+beta-2
elif stat_type=='median':
num = alpha-1/3
dem = alpha+beta-2/3
elif stat_type=='var':
num = alpha*beta
dem = (alpha+beta)**2*(alpha+beta+1)
elif stat_type=='skewness':
num = 2*(beta-alpha)*np.sqrt(alpha+beta+1)
dem = (alpha+beta+2)*np.sqrt(alpha*beta)
elif stat_type=='kurtosis':
num = 6*(alpha-beta)**2*(alpha+beta+1) - alpha*beta*(alpha+beta+2)
dem = alpha*beta*(alpha+beta+2)*(alpha+beta+3)
# replace missing
value = num/dem
value[np.isnan(value)] = np.nanmedian(value)
return value
N_min = 1000
feature_cols = []
# encode variables
for c in cat_cols:
# fit encoder
be = BetaEncoder(c)
be.fit(train, 'deal_probability')
# mean
feature_name = f'{c}_mean'
train[feature_name] = be.transform(train, 'mean', N_min)
test[feature_name] = be.transform(test, 'mean', N_min)
feature_cols.append(feature_name)
# mode
feature_name = f'{c}_mode'
train[feature_name] = be.transform(train, 'mode', N_min)
test[feature_name] = be.transform(test, 'mode', N_min)
feature_cols.append(feature_name)
# median
feature_name = f'{c}_median'
train[feature_name] = be.transform(train, 'median', N_min)
test[feature_name] = be.transform(test, 'median', N_min)
feature_cols.append(feature_name)
# var
feature_name = f'{c}_var'
train[feature_name] = be.transform(train, 'var', N_min)
test[feature_name] = be.transform(test, 'var', N_min)
feature_cols.append(feature_name)
# skewness
feature_name = f'{c}_skewness'
train[feature_name] = be.transform(train, 'skewness', N_min)
test[feature_name] = be.transform(test, 'skewness', N_min)
feature_cols.append(feature_name)
# kurtosis
feature_name = f'{c}_kurtosis'
train[feature_name] = be.transform(train, 'kurtosis', N_min)
test[feature_name] = be.transform(test, 'kurtosis', N_min)
feature_cols.append(feature_name)
5. Weight of evidence
Weight of evidence(WoE)是变量转化的利器,经常会出现在信用卡评分等问题中,用来判断好的和坏的客户。WOE不仅简单,而且可以依据其大小来筛选出重要的分组(group),可解释性较强,早期WOE和逻辑回归算法经常一起使用并且可以帮助获得较大的提升,在Kaggle的数据竞赛中,我们发现WOE和梯度提升树模型结合也可以取得不错的效果。
此处的Event和Non Event为别是标签为1的样本的分布以及标签为0的样本的分布; 标签为1的样本分布:在某个类内正样本占所有正样本的比例;标签为0的样本分布也是类似的。
从上面的公式中,我们知道,正样本的分布和负样本的分布如果在某个类中差别越大的话,涵盖的信息就越大,如果WOE的值越大,择该这个类内的为正的概率极大,反之越小。
在实践中,我们可以直接通过下面的步骤计算得到WOE的结果:
对于一个连续变量可以将数据先进行分箱,对于类别变量(无需做任何操作); 计算每个类内(group)中正样本和负样本出现的次数; 计算每个类内(group)正样本和负样本的百分比events%以及non events %; 按照公式计算WOE;
对应代码:
'''
代码摘自:https://github.com/Sundar0989/WOE-and-IV
'''
import os
import pandas as pd
import numpy as np
df = pd.read_csv('./data/bank.csv',sep=';')
dic = {'yes':1, 'no':0}
df['target'] = df['y'].map(dic)
df = df.drop('y',axis=1)
import pandas.core.algorithms as algos
from pandas import Series
import scipy.stats.stats as stats
import re
import traceback
import string
max_bin = 20
force_bin = 3
# define a binning function
def mono_bin(Y, X, n = max_bin):
df1 = pd.DataFrame({"X": X, "Y": Y})
justmiss = df1[['X','Y']][df1.X.isnull()]
notmiss = df1[['X','Y']][df1.X.notnull()]
r = 0
while np.abs(r) < 1:
try:
d1 = pd.DataFrame({"X": notmiss.X, "Y": notmiss.Y, "Bucket": pd.qcut(notmiss.X, n)})
d2 = d1.groupby('Bucket', as_index=True)
r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)
n = n - 1
except Exception as e:
n = n - 1
if len(d2) == 1:
n = force_bin
bins = algos.quantile(notmiss.X, np.linspace(0, 1, n))
if len(np.unique(bins)) == 2:
bins = np.insert(bins, 0, 1)
bins[1] = bins[1]-(bins[1]/2)
d1 = pd.DataFrame({"X": notmiss.X, "Y": notmiss.Y, "Bucket": pd.cut(notmiss.X, np.unique(bins),include_lowest=True)})
d2 = d1.groupby('Bucket', as_index=True)
d3 = pd.DataFrame({},index=[])
d3["MIN_VALUE"] = d2.min().X
d3["MAX_VALUE"] = d2.max().X
d3["COUNT"] = d2.count().Y
d3["EVENT"] = d2.sum().Y # 正样本
d3["NONEVENT"] = d2.count().Y - d2.sum().Y # 负样本
d3 = d3.reset_index(drop=True)
if len(justmiss.index) > 0:
d4 = pd.DataFrame({'MIN_VALUE':np.nan},index=[0])
d4["MAX_VALUE"] = np.nan
d4["COUNT"] = justmiss.count().Y
d4["EVENT"] = justmiss.sum().Y
d4["NONEVENT"] = justmiss.count().Y - justmiss.sum().Y
d3 = d3.append(d4,ignore_index=True)
d3["EVENT_RATE"] = d3.EVENT/d3.COUNT # 正样本类内百分比
d3["NON_EVENT_RATE"] = d3.NONEVENT/d3.COUNT # 负样本类内百分比
d3["DIST_EVENT"] = d3.EVENT/d3.sum().EVENT # 正的样本占所有正样本百分比
d3["DIST_NON_EVENT"] = d3.NONEVENT/d3.sum().NONEVENT # 负的样本占所有负样本百分比
d3["WOE"] = np.log(d3.DIST_EVENT/d3.DIST_NON_EVENT)
d3["IV"] = (d3.DIST_EVENT-d3.DIST_NON_EVENT)*np.log(d3.DIST_EVENT/d3.DIST_NON_EVENT)
d3["VAR_NAME"] = "VAR"
d3 = d3[['VAR_NAME','MIN_VALUE', 'MAX_VALUE', 'COUNT', 'EVENT', 'EVENT_RATE', 'NONEVENT', 'NON_EVENT_RATE', 'DIST_EVENT','DIST_NON_EVENT','WOE', 'IV']]
d3 = d3.replace([np.inf, -np.inf], 0)
d3.IV = d3.IV.sum()
return(d3)
def char_bin(Y, X):
df1 = pd.DataFrame({"X": X, "Y": Y})
justmiss = df1[['X','Y']][df1.X.isnull()]
notmiss = df1[['X','Y']][df1.X.notnull()]
df2 = notmiss.groupby('X',as_index=True)
d3 = pd.DataFrame({},index=[])
d3["COUNT"] = df2.count().Y
d3["MIN_VALUE"] = df2.sum().Y.index
d3["MAX_VALUE"] = d3["MIN_VALUE"]
d3["EVENT"] = df2.sum().Y
d3["NONEVENT"] = df2.count().Y - df2.sum().Y
if len(justmiss.index) > 0:
d4 = pd.DataFrame({'MIN_VALUE':np.nan},index=[0])
d4["MAX_VALUE"] = np.nan
d4["COUNT"] = justmiss.count().Y
d4["EVENT"] = justmiss.sum().Y
d4["NONEVENT"] = justmiss.count().Y - justmiss.sum().Y
d3 = d3.append(d4,ignore_index=True)
d3["EVENT_RATE"] = d3.EVENT/d3.COUNT
d3["NON_EVENT_RATE"] = d3.NONEVENT/d3.COUNT
d3["DIST_EVENT"] = d3.EVENT/d3.sum().EVENT
d3["DIST_NON_EVENT"] = d3.NONEVENT/d3.sum().NONEVENT
d3["WOE"] = np.log(d3.DIST_EVENT/d3.DIST_NON_EVENT)
d3["IV"] = (d3.DIST_EVENT-d3.DIST_NON_EVENT)*np.log(d3.DIST_EVENT/d3.DIST_NON_EVENT)
d3["VAR_NAME"] = "VAR"
d3 = d3[['VAR_NAME','MIN_VALUE', 'MAX_VALUE', 'COUNT', 'EVENT', 'EVENT_RATE', 'NONEVENT', 'NON_EVENT_RATE', 'DIST_EVENT','DIST_NON_EVENT','WOE', 'IV']]
d3 = d3.replace([np.inf, -np.inf], 0)
d3.IV = d3.IV.sum()
d3 = d3.reset_index(drop=True)
return(d3)
def data_vars(df1, target):
stack = traceback.extract_stack()
filename, lineno, function_name, code = stack[-2]
vars_name = re.compile(r'\((.*?)\).*$').search(code).groups()[0]
final = (re.findall(r"[\w']+", vars_name))[-1]
x = df1.dtypes.index
count = -1
for i in x:
if i.upper() not in (final.upper()):
if np.issubdtype(df1[i], np.number) and len(Series.unique(df1[i])) > 2:
conv = mono_bin(target, df1[i])
conv["VAR_NAME"] = i
count = count + 1
else:
conv = char_bin(target, df1[i])
conv["VAR_NAME"] = i
count = count + 1
if count == 0:
iv_df = conv
else:
iv_df = iv_df.append(conv,ignore_index=True)
return iv_df
final_iv = data_vars(df,df.target)
6. 人工编码
6.1 人工转化编码:
这个需要一些专业背景知识,可以认为是Label编码的一种补充,如果我们的类别特征是字符串类型的,例如:
城市编号:'10','100','90','888'...
这个时候,我们使用Labelencoder会依据字符串排序编码。在字符串中'90' > '100',但我们直观感觉是为'100' > '90',所以需要人为但进行干预编码,如果都是可以直接转化为数值形的,编码时可以直接转化为数值,或者自己书写一个字典进行映射。
6.2 人工组合编码:
这个同样的也设计到部分专业背景知识,有些问题会出现一些脏乱的数据,例如:
在一些位置字段中,有的是中文的,有的是英文的,例如“ShangHai”,“上海”,二者描述的是同一个地方,但如果我们不注意就忽略了;
这个时候,我们可以先采用字典映射等方式对其进行转化,然后再使用上面所属的Frequency等编码重新对其进行处理。
7. 扩展
上面是数据竞赛中最为常用的编码特征,在基于梯度提升树模型的建模中,上面的编码往往可以带来非常大的帮助,也都是非常值得尝试的。当然还有一些其它的类别特征的编码形式,目前使用较多的一个库就是category_encoders,有兴趣的朋友可以当作扩展进行学习,此处不再叙述。
往期精彩回顾
本站qq群851320808,加入微信群请扫码:
