每日一道 LeetCode (16):求 x 的平方根

❝每天 3 分钟,走上算法的逆袭之路。
❞
前文合集
代码仓库
GitHub:https://github.com/meteor1993/LeetCode
Gitee:https://gitee.com/inwsy/LeetCode
题目:求 x 的平方根
题目来源:https://leetcode-cn.com/problems/sqrtx/
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4
输出: 2
示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842...,
由于返回类型是整数,小数部分将被舍去。
解题过程
看到这道题,嗯,实际上我是完全不会做的,只能说有一个初步的想法,但是感觉太二了,也就没写代码,直接去翻答案了。
看到答案以后,悄悄的讲,理解起来稍微还有点难度。
讲老实话,这道题,如果没点高中数学的知识,还真的是做不出来。
但是如果把高中数学的知识给各位普及一下,我感觉应该还不算是难做的。
问题的关键就是,高中数学老师的棺材板都要压不住了。

官方解法一:袖珍计算器算法
这种解法官方还给了一个看起来很高大上的名字 「袖珍计算器算法」 ,实际上我看下来感觉就是使用数学公式偷换概念。
这种方案并不介意各位同学在面试的时候拿出来用,否则被面试官按在地上摩擦就不好了。
目标是要求根号 x ,然后在公式上做了一个骚操作。
看不懂的同学去面壁,这个我记得不错的话应该是初中数学。
总体思路就是用自然对数 e 进行换底,讲道理,这题我上初中的时候应该能想到,现在已经完全没有任何想法了。
公式给了代码实际上就很简单了:
public int mySqrt(int x) {
if (x == 0) return 0;
int ans = (int) Math.exp(0.5 * Math.log(x));
return (long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans;
}
直接用数学公式解答,果然是最快的方案。
官方解法二:二分法
二分法其实就是我一开始想到的方案,用 n * n 不停的去试,直到试到 n * n < x && (n + 1) * (n + 1) > x 或者正好 n * n = x 。
然后接下来就是使用二分查找找到这个数 n ,首先定义最左边的书是 0 ,最右边的数是 x 。
因为 x 开平方肯定是小于等于自己的,然后用二分法一步一步查找下去,直到找到那个数,代码如下:
public int mySqrt_1(int x) {
if (x == 0) return 0;
int left = 0, right = x, ans = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if ((long) mid * mid <= x) {
ans = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return ans;
}
这里的 (long) mid * mid 这一段代码要注意,因为 mid 本身是 int ,做乘法以后,如果够大和容易超出上限的,所以这里做了类型强转,转成了 long 类型。
二分查找次数稍微有点多,毕竟很多数开平方后差距都是会少很多数量级的(越大的数少的越多),即使使用二分法要找到也需要循环更多的次数。
官方解法三:牛顿迭代
这个名词我是第一次听,不过从名字上就可以看出来,这个方法又是我们伟大的牛顿老师发明的。
顺便说一句,我在学微积分的时候就已经恨死他了。
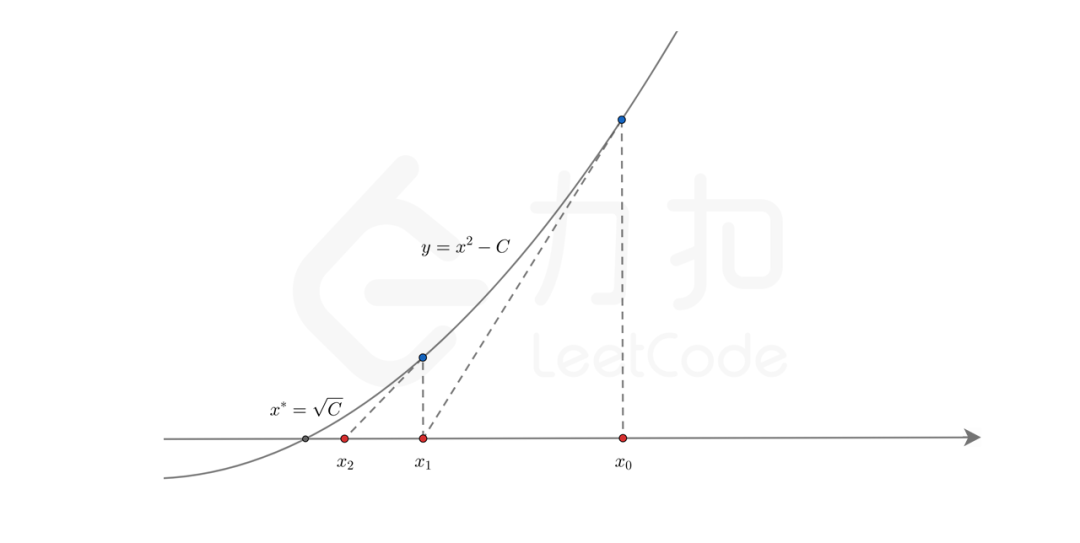
牛顿迭代的思想是借助泰勒级数,从初始值开始快速向零点逼近。
任取一个 作为初始值,在每一步的迭代中,我们找到函数图像上的点 ,过该点作一条斜率为该点导数 的直线,与横轴的交点记为 。 相较于 而言距离零点更近。在经过多次迭代后,我们就可以得到一个距离零点非常接近的交点。
「算法」
我们选择 作为初始值。
在每一步迭代中,我们找到 在图像上对应的点 作一条斜率为 的直线,直线的方程为:
与横轴的交点实际上就是上面那个方程 y = 0 的解,即为新的迭代结果 :
在进行 k 次迭代后, 的值与真实的零点 足够接近,即可作为答案。
上面这段内容好好理解一下,我也是看了很久才看懂几个公式的推导,真的是全都忘光了。
代码我还是抄一下官方的代码吧,做一个参考:
public int mySqrt_2(int x) {
if (x == 0) return 0;
double C = x, x0 = x;
while (true) {
double xi = 0.5 * (x0 + C / x0);
if (Math.abs(x0 - xi) < 1e-7) {
break;
}
x0 = xi;
}
return (int) x0;
}
可以看到,牛顿迭代的效率也是极高的,几乎可以媲美我们直接由数学公式推导。
这里有个小问题需要注意下,我们迭代到什么程度可以结束?一般是选取一个极小值,一般取到 或者 。
参考
https://leetcode-cn.com/

