每日一道 LeetCode (15):二进制求和

❝每天 3 分钟,走上算法的逆袭之路。
❞
前文合集
代码仓库
GitHub:https://github.com/meteor1993/LeetCode
Gitee:https://gitee.com/inwsy/LeetCode
题目:数组加一
题目来源:https://leetcode-cn.com/problems/add-binary/
给你两个二进制字符串,返回它们的和(用二进制表示)。
输入为 非空 字符串且只包含数字 1 和 0。
示例 1:
输入: a = "11", b = "1"
输出: "100"
示例 2:
输入: a = "1010", b = "1011"
输出: "10101"
提示:
每个字符串仅由字符 '0' 或 '1' 组成。 1 <= a.length, b.length <= 10^4 字符串如果不是 "0" ,就都不含前导零。
解题过程
方案一:偷鸡方法
每天做题就像一个开盲盒的过程,没开始之前,永远都不知道会遇到什么样的题目。
这道题我第一眼看过去,二进制加法?不会,我才不要自己去写一个二进制加法出来, Java 给我们提供了现成的 math 函数包,是用来看的么?
果断第一个想法是先把二进制转成十进制,做完加法以后再转回去做输出。
我就是个小机灵鬼。
public String addBinary(String a, String b) {
return decimalToBinary(binaryToDecimal(a).add(binaryToDecimal(b)));
}
// 定义二进制转十进制
private BigInteger binaryToDecimal(String binarySource) {
return new BigInteger(binarySource, 2);
}
// 定义十进制转二进制
private String decimalToBinary(BigInteger decimalSource) {
return decimalSource.toString(2);
}
代码上还可以精简一点写成一行,我是怕有同学看不懂,另外定义了两个方法,比如:
public String addBinary(String a, String b) {
return (new BigInteger(a, 2).add(new BigInteger(b, 2))).toString(2);
}
结果扔到 LeetCode 上去运行,直接给我报了个编译错误。
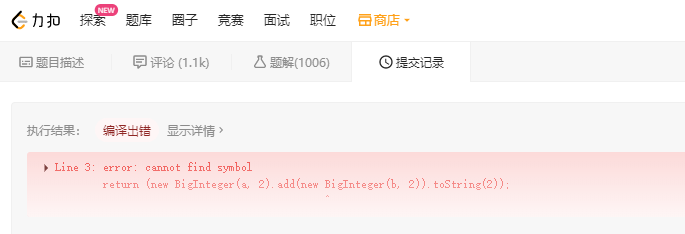
这个意思应该是不支持 BigInteger() 函数,难道我在前面加个导包?
import java.math.BigInteger;
class Solution {
public String addBinary(String a, String b) {
return (new BigInteger(a, 2).add(new BigInteger(b, 2)).toString(2));
}
}
果然添加了导包以后就正常了,就是这个执行耗时有点惨不忍睹。
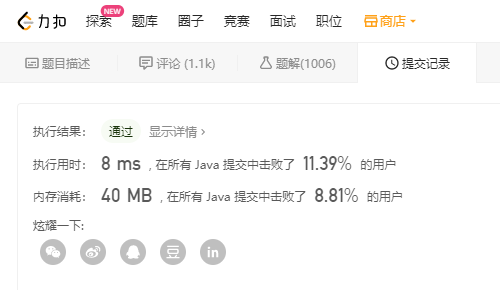
果然每次取巧的方案最后消耗时长都是最坑的,还是老老实实的想办法自己实现一下二进制加法吧。
方案二:二进制加法
二进制加法和十进制是一样的,都是从低位开始往高位运算,只不过十进制是满 10 进 1 ,而二进制是满 2 进 1 。
我们接下来要做的就是模拟一下二进制的加法过程,从低位开始计算,并且实现满 2 进 1 这个操作。
public String addBinary_1(String a, String b) {
StringBuilder sb = new StringBuilder();
// 定义进位
int pre = 0;
for (int i = a.length() - 1, j = b.length() - 1; i >= 0 || j >= 0; i--, j--) {
int sum = pre;
if (i >= 0) sum += a.charAt(i) - '0';
if (j >= 0) sum += b.charAt(j) - '0';
// 当前位添加至 sb
sb.append(sum % 2);
// 计算进位
pre = sum / 2;
}
// 进位如果为 1 则添加到 sb 上
if (pre == 1) sb.append('1');
// 反转字符串输出
return sb.reverse().toString();
}
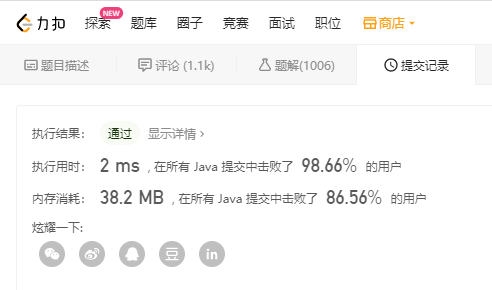
上面这个算法其中有一点需要注意,就是为什么要做 a.charAt(i) - '0' 这样一步操作,因为直接通过 a.charAt(i) 取出来的是当前字符的 ASCII 值, 0 的 ASCII 值是 48 ,而 1 的 ASCII 值是 49 ,用这两个值都去减 '0' ,正好得到了我们需要的 1 或者 0 。
其余的计算当前位是取模,计算进位是做除法,这两个就不多说了,很常规的用法。

