不能说每个深耕机器学习的人都学过吴恩达的《机器学习》课程,但他的这门课确是目前让机器学习初学者能够快速对整个体系知识点有比较整体的认识,便于快速入门的首选及最热课程。
根据2019年Freecodecamp的统计,这门课是所有在线Machine Learning课程中最受到大家好评的课程。
Coursera上评分4.9,现已有有超15万个评分及近4万条评论
例如,不少网友在知乎上讨论,“说好的是入门级课程,怎么听着很费解啊?”不是的!说这门课难的发言里,看得出来,大多卡在了“数学”上。甚至这类学习者本人并没有意识到原因:“我觉得对有点点基础的人,不必刻意学习数学,看ML的教材时候不懂的再去查,重心应该放在实战上。”所以,学吴恩达的课程真的不需要“刻意学习数学”吗?再深究一下,机器学习真的不需要数学基础吗?吴恩达的机器学习课程笼统主要指这两门,一门是Cousera上的课程Machine Learning | Coursera,一门是斯坦福大学的课程CS229:Machine Learning,国内讨论较多的是前者。有人在Github开源了吴恩达MachineLearning个人笔记,用Python复现了课程作业,星数超2万,下载超100万次。面对这份干货满满的笔记,制作者收到反馈:“很多同学说看不懂公式。”
是不是感觉这个配方很熟悉!说白了,还是数学底子不够啊。
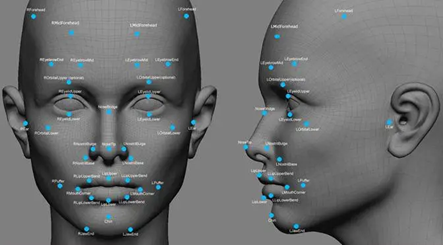
“我增加了数学基础作为附件放在笔记里。”在最新一个版本里,制作者针对大家的问题,增加了数学基础笔记。此外,吴恩达在斯坦福大学开设的CS229课程,他在第一次课上便讲到了先修要求:他假定上课的人都是有一定数学基础的。可见,不是入门级经典课程太难,而是这个课程真的是需要大家有一定的数学基础。数学在机器学习中非常重要,不论是在算法上理解模型代码,还是在工程上构建系统,数学都必不可少。尽管机器学习的普及已经促使 Python 和 R 产生了许多易于使用并得到广泛支持的库,它们提供了某种机器学习的捷径,似乎绕过了这类操作所需算法背后的数学。然而,机器学习背后的数学原理基本不变。宾夕法尼亚大学计算机系教授Jean Gallier主编了一本机器学习的“数学全书”, Algebra,Topology, Differential Calculus, and Optimization Theory For Computer Scienceand Engineering,中文名为《计算机科学和机器学习相关代数、拓扑学、微分学和最优化理论》,用了1900余页来阐述机器学习所需的数学知识。机器学习是集合了统计学、概率论、计算机科学、数学算法多等方面交叉研究,即便对机器学习的应用炉火纯青,但对这些技术没有一个全面的数学理解,也极有可能出现应用失误。机器学习严重依赖于数学。为什么这么说,从依赖于机器学习的人脸识别算法这一例子来具体理解一下:示例数据集中的图像像素以向量的形式存储在矩阵中。这利用到了线性代数。如果拍摄彩色图像的话,那么根据使用的颜色方案使用若干个矩阵,并将每个像素的强度存储在这些向量中。这使得处理数据变得容易,并且便于对它们进行向量操作,将现有的人脸与给定图片中的人脸进行比较。用微积分可以解决当前误差的梯度。绘制出人脸的定义与给定图片之间的误差梯度。如果梯度超过容许限度,则通过更新其存储的向量的系数来更新人脸的定义。任何算法都不能给出100%可靠的输出。因此,要使用概率来判定给定图片是否存在人脸。概率将输入与算法的容限因子进行比较。统计学贯穿于算法所经历的各个过程,也被用来检验假设,该假设是给定图像存在人脸,并且检验结果显示虚假设(null hypotheses)或备择假设(alternative hypotheses)是否被接受。数学决定了开发人员的上限,就机器学习这一领域而言,若想走得更长远,那真的要储备并深刻理解一些数学知识。想深耕机器学习,开发人员应具备哪些数学知识?并且如何学好数学呢?推荐雷明老师编写的《机器学习的数学》一书。本书的目标是帮助读者全面、系统地学习机器学习所必需的数学知识。全书由8章组成,内容包括微积分、线性代数与矩阵论、最优化方法、概率论、信息论、随机过程、以及图论。本书从机器学习的角度讲授这些数学知识,对它们在该领域的应用举例说明,使读者对某些抽象的数学知识和理论的实际应用有直观、具体的认识。本书内容紧凑,结构清晰,深入浅出,讲解详细,可用作计算机、人工智能、电子工程、自动化、数学等相关专业的教材与教学参考书。对人工智能领域的工程技术人员与产品研发人员,本书也有很强的参考价值。对于广大数学与应用的数学爱好者,本书亦为适合自学的读本。雷明,SIGAI联合创始人&CEO,是人工智能和机器学习领域的资深专家。毕业于清华大学计算机系,获得研究生学位。雷明是前百度工程师、项目经理,有超过12年的机器学习、机器视觉、自然语言处理方面的丰富经验。https://zh.coursera.org/learn/machine-learninghttps://www.freecodecamp.org/news/every-single-machine-learning-course-on-the-internet-ranked-by-your-reviews-3c4a7b8026c0/https://www.zhihu.com/question/65780182https://zhuanlan.zhihu.com/p/43637164https://www.zhihu.com/question/66734784/answer/1204003247https://github.com/fengdu78/Coursera-ML-AndrewNg-Noteshttps://mp.weixin.qq.com/s/IlyQpJpezMG9y37aBk2m-whttp://cs229.stanford.edu/https://www.dspwj.cn/archives/654https://medium.com/analytics-vidhya/role-of-mathematics-in-machine-learning-f070e7cf6128
关注公众号《AI算法与图像处理》,并回复“数学”,即可参与活动






 下载APP
下载APP







