知乎热议：高数、线代应该成为计算机专业学习的重心吗？-技术圈

作为一名计算机专业的学生，你觉得求学期间哪门课程最重要？

你又将哪门课程作为学习的重中之重呢？

总有人推荐计算机学生把重点放在高数和线代?

你觉得呢？

考研党的心声：该学还得学

众所周知，计算机是一个非常宽泛的学科，学生毕业后所从事的领域也五花八门，例如有操作系统，编译，数据库，逆向工程，信息安全，甚至还有软件工程等等。

那么，这些领域都需要，或者说很需要高数与线代吗？

想必本专业的学生，此时脑中蹦出了四个大字：离、散、数、学。

包括非ML的传统算法在内，CS的大部分方向依赖的是数理逻辑和图论之类的数学分支，具体到大学本科课程对应的也是离散数学，而不是高数。

但是，作为计算机本科生，这是大家放弃高数和线代的理由吗？

或许一个更为庞大的群体：考研党，会给出不一样的答案。

在刚刚过去的2020年，计算机硕士继续呈现「爆炸」增长。以如今计算机的缺口，本科毕业生根本无法填充，再加上计算机的就业路比较宽，半路出家考研的也大有人在。所以，作为考研必考科目的高数与线代，当然也是非学不可。

除了应试，我们还要关注作为数学基础，它们有着培养数学思维的作用。

数学思维对计算机行业，或者说一切理工科都有着无与伦比的重要性。

如今各种软件，都与数学有必然的联系，例如在游戏、图形软件开发中引用了线性代数中大量的坐标变换，矩阵运算。而对开发游戏引擎，人工智能算法来说，数学更是根基，不但开发引擎需要数学知识，开发游戏逻辑也需要，所需知识就基本覆盖了大学里《高等数学》、《线性代数》、《概率与数理统计》等课程。

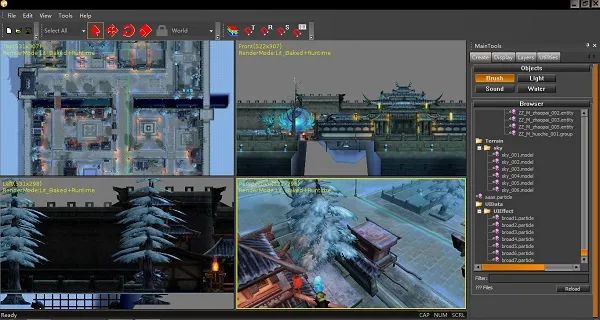
岗位上用到高数多少？

但也有人认为，聚焦数学固然重要，但不要过分夸大高数与线代的重要性。

因为像人工智能岗位、游戏引擎开发岗位等等，还并不能代表程序员群体的全部。

还是回到应用更为广泛的离散数学身上，计算机本身的存储结构是离散的。

所以很多时候，没必要过分强调「基础论」，因为从计算机系统的角度讲，大都依赖的是离散结构的数学，而非微分方程。

不是学习C/C++方向和考研，没有太大的必要把学习精力重点放在高数和线代上面。你更应该学好计算机网络、操作系统、数据库、数据结构与算法等等计算机科学相关内容，和编程语言以及用编程语言开发出具体的项目上。

罗杰·培根曾说，「数学是科学的大门和关键。」

当提到数学时，大多数人通常会想到需要数字并且专注于计算某种值：

但是，要认识到，数学涉及的不止是数字，它还涵盖了广泛的主题：

而且很明显的是，在一个程序员不了解某些数学理论的情况下，他的编程内容极有可能受限。

IT部门需要大量程序员来创建可自动化或简化业务逻辑的应用程序。这些是业务线应用程序，它们为公司用户提供了更有效地完成工作所需的信息。这项工作大部分围绕大型数据库进行，并将数据集缩减为用户所需的相关信息。

机器和尖端技术的软件工程通常确实需要高级数学知识。在过去的20年中，已发展并成为主流的所有无线技术都严重依赖于信号处理算法。信号处理本身可以涵盖波形合成和分析，压缩，加密，前向纠错和调制/解调。

现在考虑人工智能，计算机视觉，图像处理，自然语言处理，模拟，机器人技术，通用GPU编程，分布式计算，并且每年都在继续增长。除了机器人技术，智能手机也在某种程度上取决于上述技术，所有这些技术都需要具备高级数学知识才能很好地完成。

大多数网站不会收到大量无法通过增加硬件解决问题的流量。但是，即使如今硬件的商品价格上涨，更多的硬件也不永远是最好的，甚至也不是简单的解决方案。

具有强大的批判性思维和推理能力的经验丰富的开发人员，才是最重要的。例如，对于像Facebook这样的公司来说，随着全球不断发生的数亿次互动，就更需要高度专业化的算法来尽可能高效地运营网站。

最后引用一句知乎网友的话，让我们回到现实：

参考知乎网友回答：

https://www.zhihu.com/question/403076697?utm_source=wechat_session&utm_medium=social&utm_oi=91028414010295500

8&utm_content=group3_supplementQuestions&utm_campaign=shareopn

版权申明：内容来源网络，版权归原创者所有。除非无法确认，我们都会标明作者及出处，如有侵权烦请告知，我们会立即删除并表示歉意。谢谢!

感谢阅读