数学趣谈: 商群到底是个什么玩意儿?

本篇介绍一点群论知识，为后文将要介绍的矩阵群、李群等知识打个底。继续下文之前，先看几个定义热热身。

1定义

群 : 给集合 中的元素定义一个二元运算，即乘法 ，但是这种运算需要满足如下 4 个性质才能构成群，

• 封闭性: 集合中任意两个元素 的乘积仍然在这个集合中，即 ；
• 结合律: ；
• 幺元/单位元: 集合中存在元素 ，对于任意 都有 ，则 被称为幺元或单位元；
• 逆元: 集合中任意元素 ，存在集合中的元素 ，使得 ， 与 互为逆元。

注意这 4 条的头 4 个字: 封结幺逆，自己想个办法记一记。比如，是不是听起来有点像封建妖孽或者凤姐妖孽。

注意，这里的每一条都是重要的，比如第一条: 这个集合表示我们考虑问题时涉及的处理对象的范围，要是有些元素一相乘就跑到集合外面去了，那这个运算就没法继续玩儿了。

另外，这里的乘法是指抽象的乘法，不是小学里学的那个传统乘法运算。可以说，从群论开始，代数学的研究内容发生了根本性变化，由传统计算向结构化抽象化发展。

继续另外两个定义，

子群: 设 是群， 是 的非空子集，且 关于 上的运算 也构成群 ，则称 是 的子群。

正规子群: 设 是一个群 ， 是其子群。若 的左陪集与右陪集相等，即对于 ，都有 ， 则称 是 的正规子群或不变子群，记为 。

群 的一个子群 的两个左（右）陪集要么相同，要么不相交，即左（右）陪集的集合构成了群 的一个划分: 群中的每个元素属于且仅属于一个左（右）陪集。特别地，单位元只在一个陪集中，即 自己。因此 也是所有左（右）陪集中唯一的子群。这个划分一般称为 对 的左（右）陪集分解 （）。

对于一般的 ，集合 关于子集的积并不是一个群。对于 中的元素 、，子集的积 ，但对于 ，，不一定有 。而如果 是群 的正规子群或不变子群，那么 关于子集的积可以构成群。

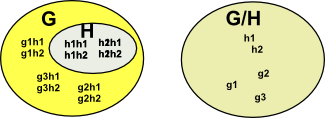
.举个栗子.

所有整数 配上加法 构成一个群，请对照群定义中的 4 条一一验证。 的一个子集 （所有能被 5 整除的整数）是 的子群，并且是它的正规子群。

群论很有用，但也挺抽象的，如果刚接触的话还是需要举一些实际例子来帮助理解。但今天这篇主要看商群，所以对于以上概念有兴趣但又第一次接触的话可以自己去翻一些参考书。

2商群

先看一下商群的定义，设 为群，而 为 的一个正规子群。

那么 是 中 的所有陪集的集合，称为 在 中的商群。

具体地，对于 中元素 和 ， 和 的乘积是 。这个运算是闭合的，因为 实际上是左陪集，

另外，对于 ，以及 和 ，有

上面都用到了 是正规子群这一点。当然严格来说，需要对照群的定义一一验证，这里从略。总之，正规子群不比一般子群，毕竟是正规部队嘛，它可以引出商群。

那么，在回答什么是商群？这个问题时。用所有陪集的集合这句话并不是很有启发性。我们认为一个更加直观的答案应该是，

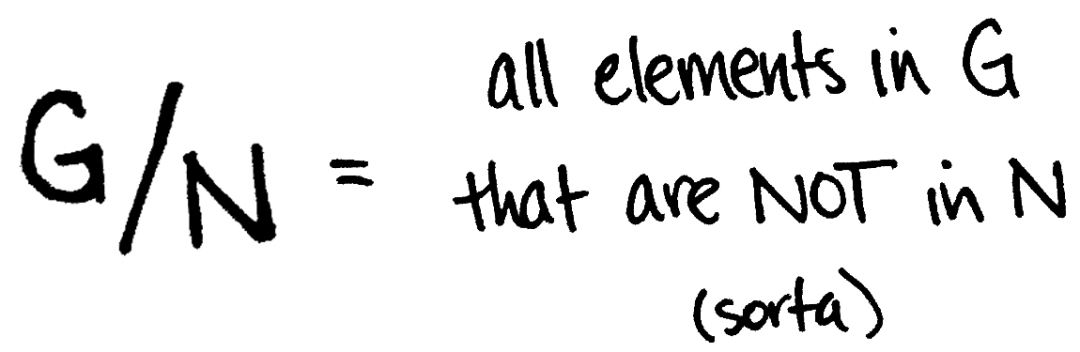
但是，让我解释一下 sorta 的含义。为了增加代入感，假设将你放入群。属于子群 只是意味着你满足某个特殊属性，例如

• 的意思是: 如果你是 的整数倍，那么就属于 。
• 的意思是: 如果你是一个元素在域 上的 可逆矩阵，并且行列式为 ，则你就在 中。”
• 的意思是: 如果你在同态 下对应单位元 ，那么你就在 中。
• 的意思是: 只要你与 的每个元素可交换，那么你就属于 （ 的中心）。
• 的意思是: 如果你是有限个元素类似 这种形式的乘积（其中，），那么你属于换位子群 。
• 等等 ...

因此，当你听到别人说形成商 之类时，真正的意思是，“请考虑 中所有不属于 的元素。” 但是总的来说，可以有很多姿势使得无法满足属于 。所以这里还有更多要说的。为了对此有所了解，我们可以想象一下对 的所有元素都可以进行问卷调查，

现在假设我们根据调查结果组织 中的元素。这个故事可能是这样的:

数学家进入一个 这个房间，跟所有元素静静地聊天，

嗨伙计。今天过得怎么样？做得好吗？太棒了。
听着，对第一个问题回答“是”的，请举手？太好了，嗨。谢谢。
现在，如果可以的话，请挤在一起。是的，就是那样。
好吧，从现在开始，你们被统称为 ，或者叫平凡陪集。
但是，抱歉，你们将不再以个人身份被关注。你们会习惯的。

数学家将注意力转移到不在 中的人群身上。

大家好。如果你为问题 #2 选择“不太糟糕”，请举手好吗？
太好了，你们的情况如何？
好。看，尽管你们都不属于 ，但是你们确实满足了另一个属性：你们都失败得不太严重（ntb）。
恭喜！现在，请在那一角围成一堆。伙计们，现在快点。好的，完美。
听着，我们不再单独关心你们了，你们对我们来说是无法区分的。
因此，你们将被称为“(ntb) N”，或者“陪集 ntb”。

接着，数学家处理房间中的剩余元素。

嗨，你们好，谢谢你们的等待。
你们中那些不属于 的人选择了“非常糟糕”（pb），请组队？
当然，你们可以站在那个角落。是的，继续。
现在，由于你们所有人都具有相同的特殊属性，因此对我们来说你们都是一样的，你们将被统称为“(pb) N”或者“陪集 pb”。

好了，我看到满足离"属于 " 的要求"差得太远"的人已经挤在一起了。
非常感谢，伙计们。现在，不要哭！这不是一件坏事。
你们将被统称为“(nec) N”或者“陪集 nec”。

此时请看下面，左图为问卷调查前，右图为调查后。

所以你看？我们可以根据元素与子群 的关系来组织整个群 。那些属于 的人还是属于 。像不太糟糕，非常糟糕和差得太远这样的标签是人为设置的，当然可以有三个以上的选项。

更进一步地说，问卷调查是根据与 的关系来组织 的成员，这也正是所谓的自然同态 所做的！ 将元素 对应到陪集 。

如果要打比喻的话，函数就像动词！他们按照某些规则做事。群同态（例如 ）也是如此，它按规则组织 的元素。

3举个栗子

并注意到 的元素可以根据它们如何满足 #1 或 #2 的方式进行分组。所产生的堆恰好是 中的陪集 。而创建堆的实际过程就是所谓的自然同态 ，它将元素 对应到陪集 。这里的代表元素 其实并没有特殊性，仅仅指示/描述如何满足 #1 或者 #2。

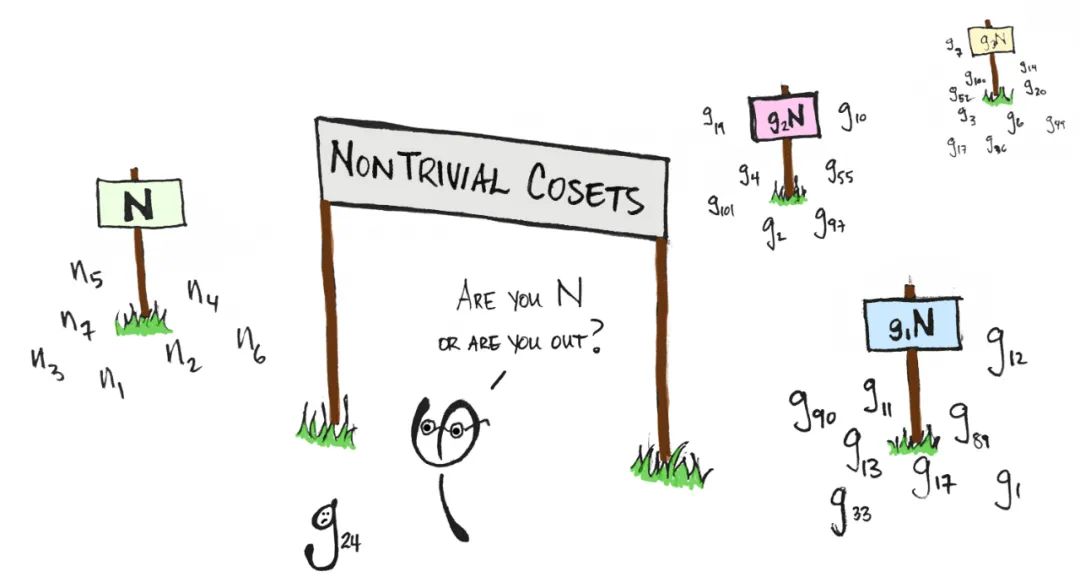
请注意，满足 #1 的情况只有一种，即你本身就属于 。但符合 #2的情况却可能有很多种，也就是说，可以存在很多种情况不满足属于 的条件。这就是为什么 仅有一个平凡陪集，却常常有多个非平凡陪集。这让我想起了一句俗语，

There are many ways to be wrong, but only one way to be right!

这就是为什么可以将 视为 中不属于 的所有元素的原因。当然， 也确实包含所有属于 的元素（毕竟，！），但是只有一种方法可以满足此条，因此，这很平凡，没有太多的有趣之处可谈。

.举个例子.

为了加深理解，我们来举个例子。例如，考虑一下 和 的情况。

我们可以将 视为不是 的倍数的所有整数，即那些不属于子群 的所有整数。如果它们以相同的原因不能归为 ，则将它们视为“相同”，

• 中的所有元素都不在 中，并且都是 1 步之遥。因此，我们称它们为陪集 。
• 中的所有元素都不在 中，并且都是 2 步之遥。因此，我们称它们为陪集 。
• 中的所有元素都不在 中，并且都是 3 步之遥。因此，我们称它们为陪集 。
• 中的所有元素都不在 中，并且都是 4 步之遥。因此，我们称它们为陪集 。

当然， 中的每个元素都是 5 的倍数。它们全都差 0 步之遥！所以我们称它们为 或简称为 。

所以你看？每个整数都可以分为两种情况: 被 5 整除或不能被 5 整除。如果不是，那么我们还可以问另一个问题: 为什么？

由于有 4 个可能的答案: 或差 1、或差 2、或差 3、或差 4，所以我们最终得到了 4 个非平凡陪集。这就是为什么   是一个阶为 5 的群: 只有 1 种姿势可以属于 ，却有 4 种姿势可以不属于。

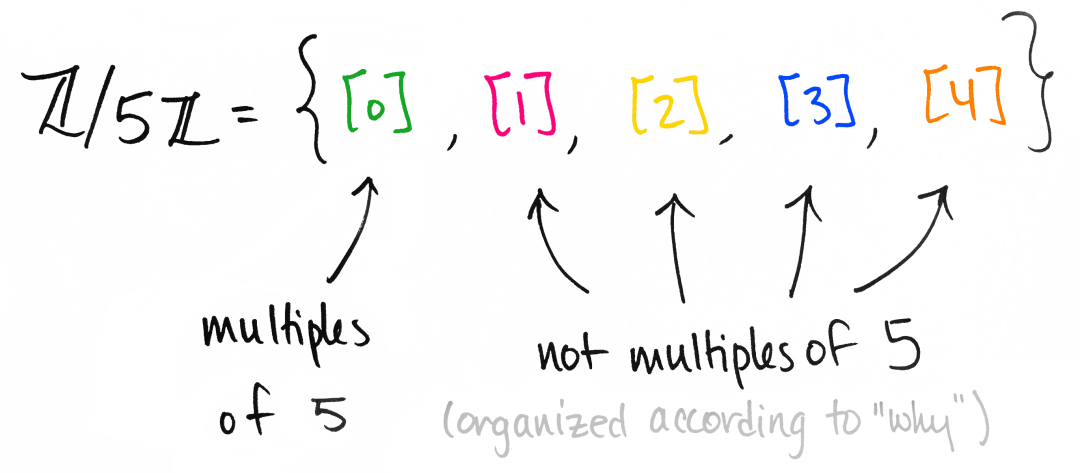
.最后一点.

细心的你可能已经注意到了，

中任意两个整数之间的差是 5 的倍数。对于 、 以及 中的任意两个整数，都可以得到同样的结论。这种作差的概念正是我们确定群中元素属于哪个陪集的精确方式。只要两个元素的差位于我们取商用到的正规子群中，它们就会被视为“相同”。

这就是教科书上说的: 假设 在 中是正规的，以及 ，那么两个陪集 和 相等当且仅当 。请注意，如果 是阿贝尔群（满足交换律的群），那么我们将 改写为 ，即 的逆加 。但是，当 不是阿贝尔群时，我们用乘替换加得到 ，这是差的乘积版本。