数据结构快速盘点 - 非线性结构

PS：为了更好的阅读体验，推荐阅读原文，到我的博客中阅读。

那么有了线性结构，我们为什么还需要非线性结构呢？ 答案是为了高效地兼顾静态操作和动态操作。大家可以对照各种数据结构的各种操作的复杂度来直观感受一下。

树

树的应用同样非常广泛，小到文件系统，大到因特网，组织架构等都可以表示为树结构，而在我们前端眼中比较熟悉的 DOM 树也是一种树结构，而 HTML 作为一种 DSL 去描述这种树结构的具体表现形式。如果你接触过 AST，那么 AST 也是一种树，XML 也是树结构。。。树的应用远比大多数人想象的要得多。

树其实是一种特殊的图，是一种无环连通图，是一种极大无环图，也是一种极小连通图。

从另一个角度看，树是一种递归的数据结构。而且树的不同表示方法，比如不常用的长子 + 兄弟法，对于 你理解树这种数据结构有着很大用处， 说是一种对树的本质的更深刻的理解也不为过。

树的基本算法有前中后序遍历和层次遍历，有的同学对前中后这三个分别具体表现的访问顺序比较模糊，其实当初我也是一样的，后面我学到了一点，你只需要记住：所谓的前中后指的是根节点的位置，其他位置按照先左后右排列即可。比如前序遍历就是根左右, 中序就是左根右，后序就是左右根， 很简单吧？

我刚才提到了树是一种递归的数据结构，因此树的遍历算法使用递归去完成非常简单，幸运的是树的算法基本上都要依赖于树的遍历。 但是递归在计算机中的性能一直都有问题，因此掌握不那么容易理解的"命令式地迭代"遍历算法在某些情况下是有用的。如果你使用迭代式方式去遍历的话，可以借助上面提到的栈来进行，可以极大减少代码量。

如果使用栈来简化运算，由于栈是 FILO 的，因此一定要注意左右子树的推入顺序。

树的重要性质：

• 如果树有 n 个顶点，那么其就有 n - 1 条边，这说明了树的顶点数和边数是同阶的。
• 任何一个节点到根节点存在唯一路径, 路径的长度为节点所处的深度

实际使用的树有可能会更复杂，比如使用在游戏中的碰撞检测可能会用到四叉树或者八叉树。以及 k 维的树结构 k-d 树等。

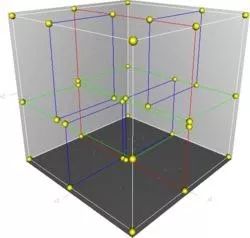（图片来自 https://zh.wikipedia.org/wiki/K-d%E6%A0%91）

二叉树

二叉树是节点度数不超过二的树，是树的一种特殊子集，有趣的是二叉树这种被限制的树结构却能够表示和实现所有的树， 它背后的原理正是长子 + 兄弟法，用邓老师的话说就是二叉树是多叉树的特例，但在有根且有序时，其描述能力却足以覆盖后者。

实际上， 在你使用长子 + 兄弟法表示树的同时，进行 45 度角旋转即可。

一个典型的二叉树：

标记为 7 的节点具有两个子节点, 标记为 2 和 6; 一个父节点,标记为 2,作为根节点, 在顶部,没有父节点。

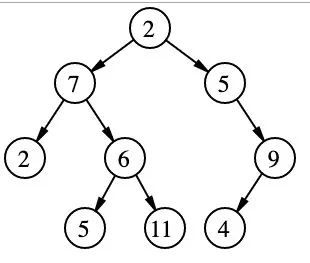
(图片来自 https://github.com/trekhleb/javascript-algorithms/blob/master/src/data-structures/tree/README.zh-CN.md)

对于一般的树，我们通常会去遍历，这里又会有很多变种。

下面我列举一些二叉树遍历的相关算法:

• 94.binary-tree-inorder-traversal
• 102.binary-tree-level-order-traversal
• 103.binary-tree-zigzag-level-order-traversal
• 144.binary-tree-preorder-traversal
• 145.binary-tree-postorder-traversal
• 199.binary-tree-right-side-view

相关概念：

• 真二叉树 （所有节点的度数只能是偶数，即只能为 0 或者 2）

另外我也专门开设了二叉树的遍历章节, 具体细节和算法可以去那里查看。

堆

堆其实是一种优先级队列，在很多语言都有对应的内置数据结构，很遗憾 javascript 没有这种原生的数据结构。 不过这对我们理解和运用不会有影响。

堆的特点：

• 在一个 最小堆(min heap) 中, 如果 P 是 C 的一个父级节点, 那么 P 的 key(或 value)应小于或等于 C 的对应值. 正因为此，堆顶元素一定是最小的，我们会利用这个特点求最小值或者第 k 小的值。

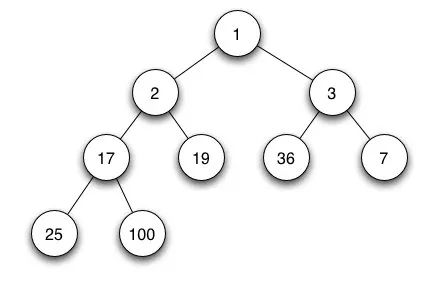
• 在一个 最大堆(max heap) 中, P 的 key(或 value)大于 C 的对应值。

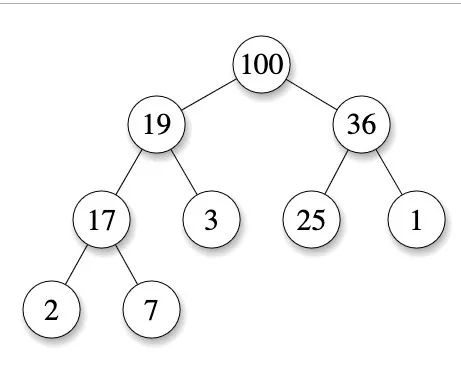
需要注意的是优先队列不仅有堆一种，还有更复杂的，但是通常来说，我们会把两者做等价。

相关算法：

• 295.find-median-from-data-stream

二叉查找树

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。

二叉查找树具有下列性质的二叉树：

• 若左子树不空，则左子树上所有节点的值均小于它的根节点的值；
• 若右子树不空，则右子树上所有节点的值均大于它的根节点的值；
• 左、右子树也分别为二叉排序树；
• 没有键值相等的节点。

对于一个二叉查找树，常规操作有插入，查找，删除，找父节点，求最大值，求最小值。

二叉查找树，之所以叫查找树就是因为其非常适合查找，举个例子， 如下一颗二叉查找树，我们想找节点值小于且最接近 58 的节点，搜索的流程如图所示：

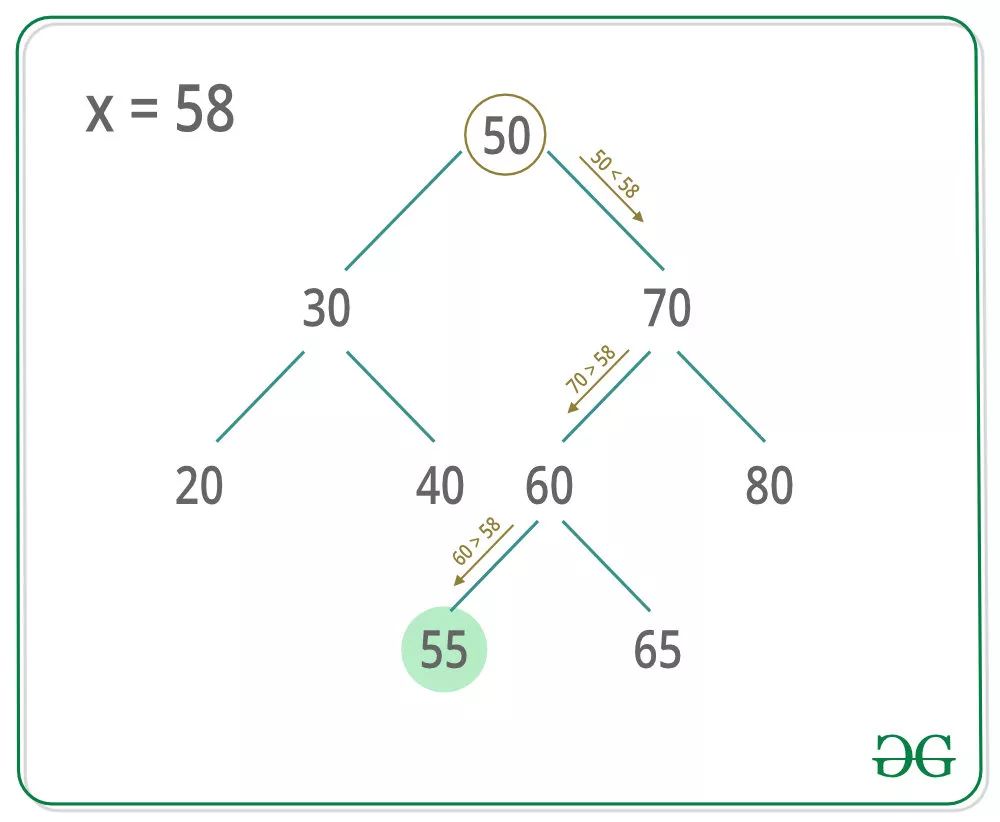（图片来自 https://www.geeksforgeeks.org/floor-in-binary-search-tree-bst/）

另外我们二叉查找树有一个性质是： 其中序遍历的结果是一个有序数组。 有时候我们可以利用到这个性质。

相关题目：

• 98.validate-binary-search-tree

二叉平衡树

平衡树是计算机科学中的一类数据结构，为改进的二叉查找树。一般的二叉查找树的查询复杂度取决于目标结点到树根的距离（即深度），因此当结点的深度普遍较大时，查询的均摊复杂度会上升。为了实现更高效的查询，产生了平衡树。

在这里，平衡指所有叶子的深度趋于平衡，更广义的是指在树上所有可能查找的均摊复杂度偏低。

一些数据库引擎内部就是用的这种数据结构，其目标也是将查询的操作降低到 logn（树的深度），可以简单理解为树在数据结构层面构造了二分查找算法。

基本操作：

• 旋转

• 插入

• 删除

• 查询前驱

• 查询后继

AVL

是最早被发明的自平衡二叉查找树。在 AVL 树中，任一节点对应的两棵子树的最大高度差为 1，因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 {\displaystyle O(\log {n})} O(\log{n})。增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡。AVL 树得名于它的发明者 G. M. Adelson-Velsky 和 Evgenii Landis，他们在 1962 年的论文 An algorithm for the organization of information 中公开了这一数据结构。 节点的平衡因子是它的左子树的高度减去它的右子树的高度（有时相反）。带有平衡因子 1、0 或 -1 的节点被认为是平衡的。带有平衡因子 -2 或 2 的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。

红黑树

在 1972 年由鲁道夫·贝尔发明，被称为"对称二叉 B 树"，它现代的名字源于 Leo J. Guibas 和 Robert Sedgewick 于 1978 年写的一篇论文。红黑树的结构复杂，但它的操作有着良好的最坏情况运行时间，并且在实践中高效：它可以在 {\displaystyle O(\log {n})} O(\log{n})时间内完成查找，插入和删除，这里的 n 是树中元素的数目

字典树(前缀树)

又称 Trie 树，是一种树形结构。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

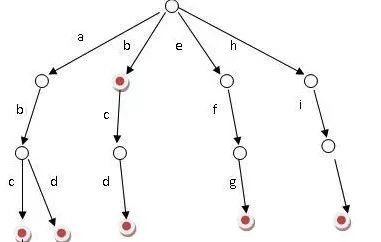
(图来自 https://baike.baidu.com/item/%E5%AD%97%E5%85%B8%E6%A0%91/9825209?fr=aladdin) 它有 3 个基本性质：

• 根节点不包含字符，除根节点外每一个节点都只包含一个字符；
• 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串；
• 每个节点的所有子节点包含的字符都不相同。

immutable 与 字典树

immutableJS的底层就是share + tree. 这样看的话，其实和字典树是一致的。

相关算法：

• 208.implement-trie-prefix-tree

图

前面讲的数据结构都可以看成是图的特例。 前面提到了二叉树完全可以实现其他树结构， 其实有向图也完全可以实现无向图和混合图，因此有向图的研究一直是重点考察对象。

图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

图的表示方法

• 邻接矩阵(常见)

空间复杂度 O(n^2),n 为顶点个数。

优点：

1. 直观，简单。

2. 适用于稠密图

3. 判断两个顶点是否连接，获取入度和出度以及更新度数，时间复杂度都是 O(1)

• 关联矩阵
• 邻接表

对于每个点，存储着一个链表，用来指向所有与该点直接相连的点 对于有权图来说，链表中元素值对应着权重

例如在无向无权图中：

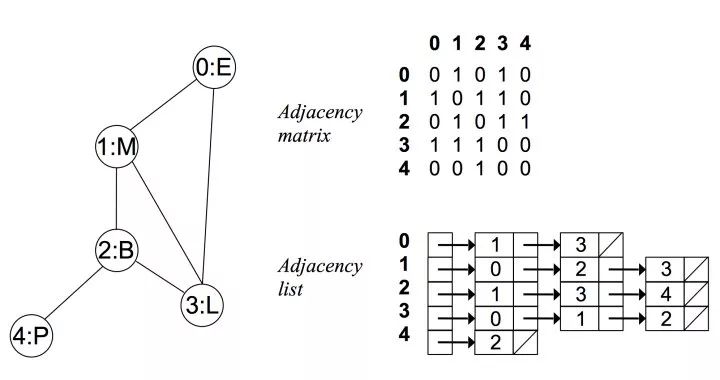（图片来自 https://zhuanlan.zhihu.com/p/25498681）

可以看出在无向图中，邻接矩阵关于对角线对称，而邻接链表总有两条对称的边 而在有向无权图中：

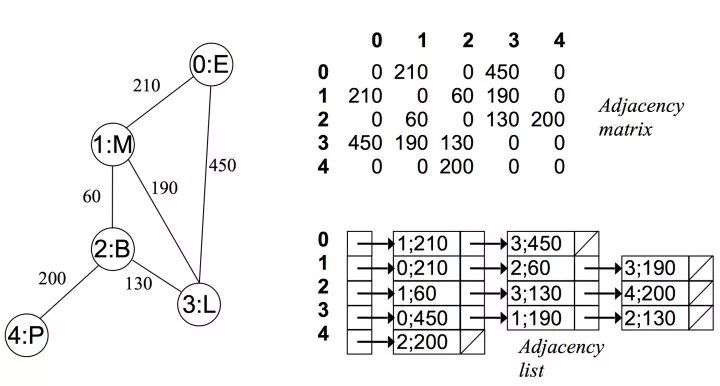
（图片来自 https://zhuanlan.zhihu.com/p/25498681）

图的遍历

图的遍历就是要找出图中所有的点，一般有以下两种方法：

1. 深度优先遍历：(Depth First Search, DFS)

深度优先遍历图的方法是，从图中某顶点 v 出发， 不断访问邻居， 邻居的邻居直到访问完毕。

1. 广度优先搜索：(Breadth First Search, BFS)

广度优先搜索，可以被形象地描述为 "浅尝辄止"，它也需要一个队列以保持遍历过的顶点顺序，以便按出队的顺序再去访问这些顶点的邻接顶点。

❤️看完三件事

如果你觉得这篇内容对你挺有启发，我想邀请你帮我三个小忙：

1. 点赞，让更多的人也能看到介绍内容（收藏不点赞，都是耍流氓-_-）
2. 关注公众号“前端劝退师”，不定期分享原创知识。
3. 也看看其他文章

劝退师个人微信：huab119

也可以来我的GitHub博客里拿所有文章的源文件：

前端劝退指南：https：//github.com/roger-hiro/BlogFN一起玩耍呀。

相关阅读：数据结构快速盘点 - 线性结构