算法与数据结构（八）图基础篇-技术圈

图（Graph）是另一种非线性表数据结构，和树比起来，图更加复杂。

我们首先了解一下图的几个关键概念：

顶点 vertex：下图中 A、B、C、D、E、F 就是顶点；
边 edge：顶点之间的连线就是边，边可以是有向的，也可以是无向的；

我们把边有方向的图叫做“有向图”；
没有方向的图就叫做“无向图”；
在带权图中，每条边有一个权重 weight；

度 degree：顶点的度是指与该顶点相关联的边的条数；

在有向图中，我们把度分为入度和出度；
入度是指指向该顶点的边的数量；
出度是指由该顶点指向其他顶点的边的数量；

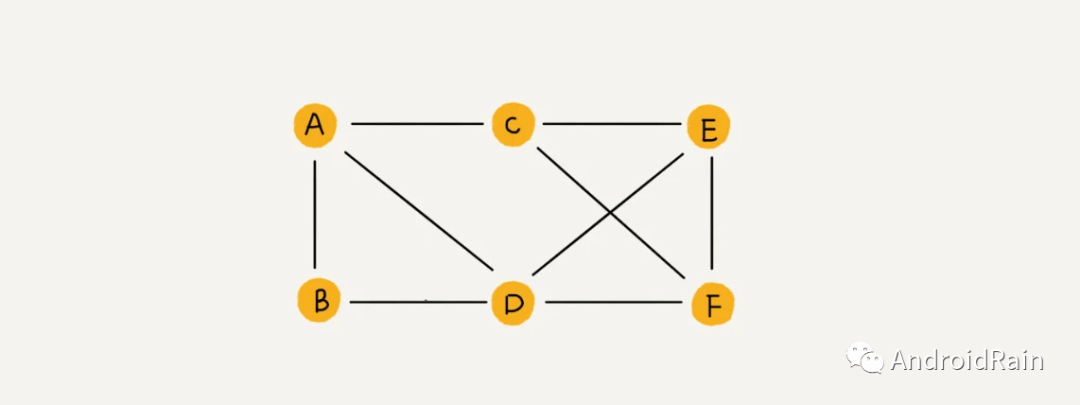
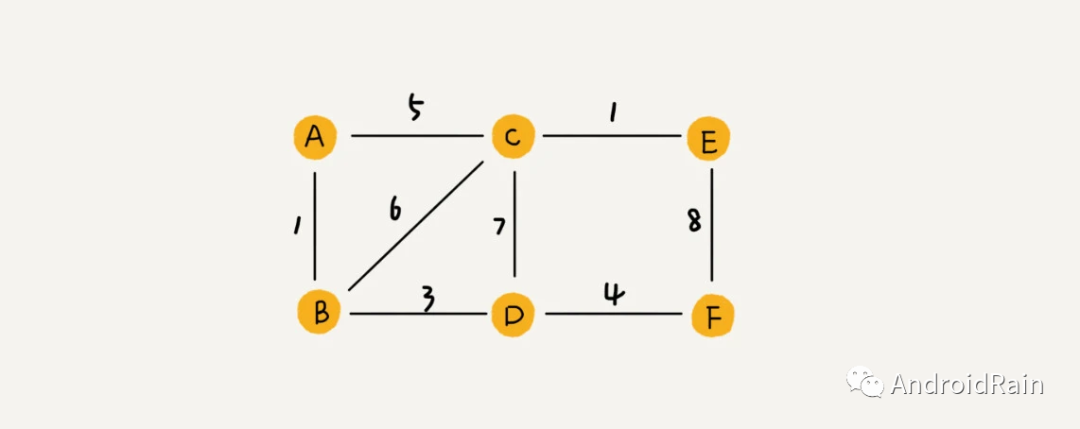
图一般用在描述事物之间的关系，比如社交网络中的用户之间的关系、城市之间的交通等等。有向图可以表示社交网络中用户之间的关注关系，无向图可以表示用户之间的好友关系，带权图则可以额外表示用户之间的亲密度。

图的存储

邻接表

图的存储其中一种实现方式是邻接表，对于下图来说，邻接表的存储方式如图右边所示。

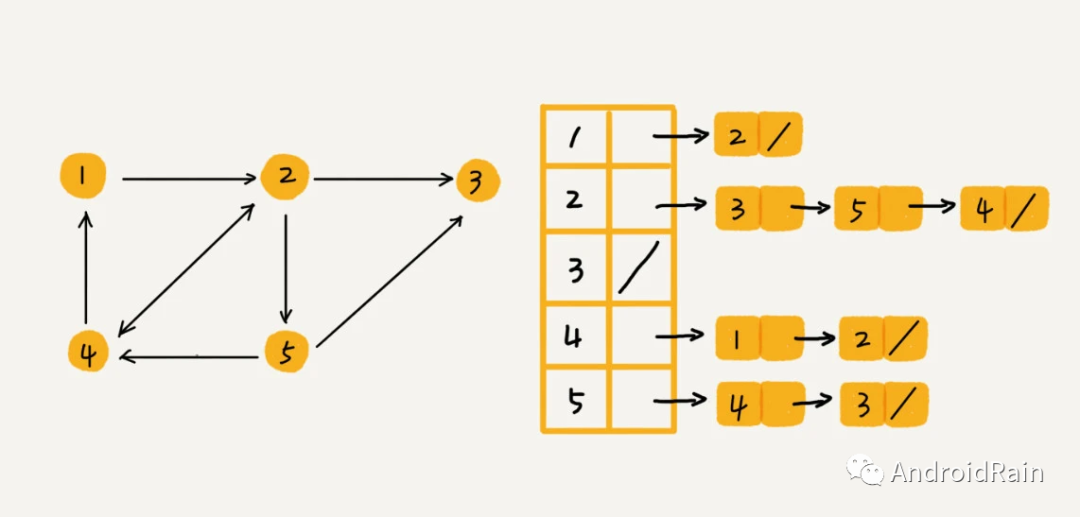
其 Java 代码表示如下：

static class Node {
    public int value;
    public ArrayList<Node> nexts;

    public Node(int value) {
        this.value = value;
        nexts = new ArrayList<>();
    }
}

邻接矩阵

图的另一种实现方式邻接矩阵，邻接矩阵的底层依赖一个二维数组。对于下图来说，邻接矩阵的存储方式如图下方所示。可以看到邻接矩阵比较浪费空间。

无向图的邻接矩阵 Java 代码表示如下：

public class Graph {
    private int v; // 顶点的个数
    private int[][] adj; // 邻接表

    public Graph(int v) {
        this.v = v;
        this.adj = new int[v][v];
        for (int i = 0; i < v; ++i) {
            adj[i][i] = 0;
        }
    }

    public void addEdge(int s, int t) { // s 先于 t，边 s->t
        adj[s][t] = 1;
    }
}

图的搜索

广度优先搜索

广度优先搜索（Breadth-First-Search，BFS）首先将根节点放入队列中，然后从其子节点开始，依次将子节点放入队列的末尾。它在遍历同一层上的所有节点之前，不会遍历下一层的节点。

广度优先算法可以解决两类问题：

从节点 A 出发，有没有前往节点 B 的路径；
从节点 A 出发，前往节点 B 的最短路径是什么。

广度优先搜索的时间复杂度是 O(V+E)，其中 V 表示顶点的数量，E 表示边的数量。以下是图广度优先搜索的 Java 代码表示，在遍历的过程中，需要借助队列这一数据结构：

public static void bfs(Node node) {
    if (node == null) return;
    Queue<Node> queue = new LinkedList<>();
    Set<Node> visited = new HashSet<>();
    queue.add(node);
    visited.add(node);
    while (!queue.isEmpty()) {
        Node cur = queue.poll();
        System.out.println(cur.value);
        for (Node next : cur.nexts) {
            if (!visited.contains(next)) {
                queue.add(next);
                visited.add(next);
            }
        }
    }
}

深度优先搜索

深度优先搜索（Depth-First-Search，DFS）使用的是回溯思想，会优先遍历当前节点的子节点，而不是邻居节点。

深度优先搜索的时间复杂度是 O(V+E)，其中 V 表示顶点的数量，E 表示边的数量。以下是图深度优先搜索的递归 Java 代码表示。在遍历的过程中，如果不采用递归，则需要栈这一数据结构来辅助遍历：

// 递归实现
public static void dfs(Node s) {
    Set<Node> visited = new HashSet<>();
    recurDfs(s, visited);
}

private static void recurDfs(Node node, Set<Node> visited) {
    visited.add(node);
    System.out.println(node.value);
    for (Node q : node.nexts) {
        if (!visited.contains(q)) {
            recurDfs(q, visited);
        }
    }
}

// 非递归实现
public static void dfsWithStack(Node s) {
    Stack<Node> stack = new Stack<>();
    Set<Node> visited = new HashSet<>();

    stack.add(s);
    visited.add(s);
    while (!stack.isEmpty()) {
        Node cur = stack.pop();
        System.out.println(cur.value);
        for (Node item : cur.nexts) {
            if (!visited.contains(item)) {
                stack.add(item);
                visited.add(item);
            }
        }
    }
}

广度优先搜索和深度优先搜索简单粗暴，没有做什么优化，仅适用于简单的图搜索问题。如果图比较大，搜索的终点离起点比较远，那这两种搜索算法就会消耗很长的时间。

算法与数据结构（八）图 基础篇

图的存储

邻接表

邻接矩阵

图的搜索

广度优先搜索

深度优先搜索

算法与数据结构（八）图基础篇