理论力学史上的明星们
日期 : 2021年09月24日
正文共 :9135字
力学是物理概念、数学方法、计算工具和实验技术以及时常还有工程目标的有机结合。理论力学课程是全部力学学科的基础,其教学内容主要是在经典力学发展阶段,也涉及少量成熟阶段的成果。古代力学主要有历史方面的意义,是构成文明史、思想史、哲学史、科学史和技术史的重要部分;经典力学奠基阶段的内容通常属于大学物理的力学部分,而成熟阶段结果的系统阐述、近代力学和现代力学,基本都属于本科专业课。或研究生课程。
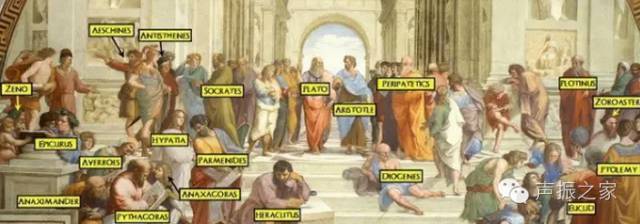
亚里士多德和雅典学院


Leonardo da Vinci, 1452-1519


Christiaan Huygens, 1629-1695
Gottfried Wilhelm Leibniz, 1646-1716

Isaac Newton, 1642-1727
3 经典力学:发展

Jacob Bernoulli, 1654-1705

Johann Bernoulli, 1667-1748

Daniel Bernoulli, 1700-1782

Pierre Varignon, 1654-1722

Leonhard Euler, 1707–1783

Jean le Rond d’Alembert, 1717-1783

Joseph Louis Lagrange, 1736-1813
4 经典力学:成熟

Louis Poinsot, 1777-1859

Gustave Gaspard Coriolis, 1792-1843

William Rowan Hamilton, 1805-1865

Jean-Bertrand-Léon Foucault, 1819-1868
5 结束语
— THE END —

评论
