A Step by Step CART Decision Tree Example-技术圈

最近看到一篇文章，关于决策树Gini系数计算的详细过程，写的非常细致清晰，分享给大家，只不过是英文版的，不过内容比较简单，看起来也不是很费劲。

原文：https://sefiks.com/2018/08/27/a-step-by-step-cart-decision-tree-example/

An algorithm can be transparent only if its decisions can be read and understood by people clearly. Even though deep learning is superstar of machine learning nowadays, it is an opaque algorithm and we do not know the reason of decision. Herein, Decision tree algorithms still keep their popularity because they can produce transparent decisions. ID3 uses information gain whereas C4.5 uses gain ratio for splitting. Here, CART is an alternative decision tree building algorithm. It can handle both classification and regression tasks. This algorithm uses a new metric named gini index to create decision points for classification tasks. We will mention a step by step CART decision tree example by hand from scratch.

We will work on same dataset in ID3. There are 14 instances of golf playing decisions based on outlook, temperature, humidity and wind factors.

Day	Outlook	Temp.	Humidity	Wind	Decision
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
3	Overcast	Hot	High	Weak	Yes
4	Rain	Mild	High	Weak	Yes
5	Rain	Cool	Normal	Weak	Yes
6	Rain	Cool	Normal	Strong	No
7	Overcast	Cool	Normal	Strong	Yes
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
10	Rain	Mild	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes
12	Overcast	Mild	High	Strong	Yes
13	Overcast	Hot	Normal	Weak	Yes
14	Rain	Mild	High	Strong	No

Gini index

Gini index is a metric for classification tasks in CART. It stores sum of squared probabilities of each class. We can formulate it as illustrated below.

Gini = 1 – Σ (Pi)2 for i=1 to number of classes

Outlook

Outlook is a nominal feature. It can be sunny, overcast or rain. I will summarize the final decisions for outlook feature.

Outlook	Yes	No	Number of instances
Sunny	2	3	5
Overcast	4	0	4
Rain	3	2	5

Gini(Outlook=Sunny) = 1 – (2/5)2 – (3/5)2 = 1 – 0.16 – 0.36 = 0.48

Gini(Outlook=Overcast) = 1 – (4/4)2 – (0/4)2 = 0

Gini(Outlook=Rain) = 1 – (3/5)2 – (2/5)2 = 1 – 0.36 – 0.16 = 0.48

Then, we will calculate weighted sum of gini indexes for outlook feature.

Gini(Outlook) = (5/14) x 0.48 + (4/14) x 0 + (5/14) x 0.48 = 0.171 + 0 + 0.171 = 0.342

Temperature

Similarly, temperature is a nominal feature and it could have 3 different values: Cool, Hot and Mild. Let’s summarize decisions for temperature feature.

Temperature	Yes	No	Number of instances
Hot	2	2	4
Cool	3	1	4
Mild	4	2	6

Gini(Temp=Hot) = 1 – (2/4)2 – (2/4)2 = 0.5

Gini(Temp=Cool) = 1 – (3/4)2 – (1/4)2 = 1 – 0.5625 – 0.0625 = 0.375

Gini(Temp=Mild) = 1 – (4/6)2 – (2/6)2 = 1 – 0.444 – 0.111 = 0.445

We’ll calculate weighted sum of gini index for temperature feature

Gini(Temp) = (4/14) x 0.5 + (4/14) x 0.375 + (6/14) x 0.445 = 0.142 + 0.107 + 0.190 = 0.439

Humidity

Humidity is a binary class feature. It can be high or normal.

Humidity	Yes	No	Number of instances
High	3	4	7
Normal	6	1	7

Gini(Humidity=High) = 1 – (3/7)2 – (4/7)2 = 1 – 0.183 – 0.326 = 0.489

Gini(Humidity=Normal) = 1 – (6/7)2 – (1/7)2 = 1 – 0.734 – 0.02 = 0.244

Weighted sum for humidity feature will be calculated next

Gini(Humidity) = (7/14) x 0.489 + (7/14) x 0.244 = 0.367

Wind

Wind is a binary class similar to humidity. It can be weak and strong.

Wind	Yes	No	Number of instances
Weak	6	2	8
Strong	3	3	6

Gini(Wind=Weak) = 1 – (6/8)2 – (2/8)2 = 1 – 0.5625 – 0.062 = 0.375

Gini(Wind=Strong) = 1 – (3/6)2 – (3/6)2 = 1 – 0.25 – 0.25 = 0.5

Gini(Wind) = (8/14) x 0.375 + (6/14) x 0.5 = 0.428

Time to decide

We’ve calculated gini index values for each feature. The winner will be outlook feature because its cost is the lowest.

Feature	Gini index
Outlook	0.342
Temperature	0.439
Humidity	0.367
Wind	0.428

We’ll put outlook decision at the top of the tree.

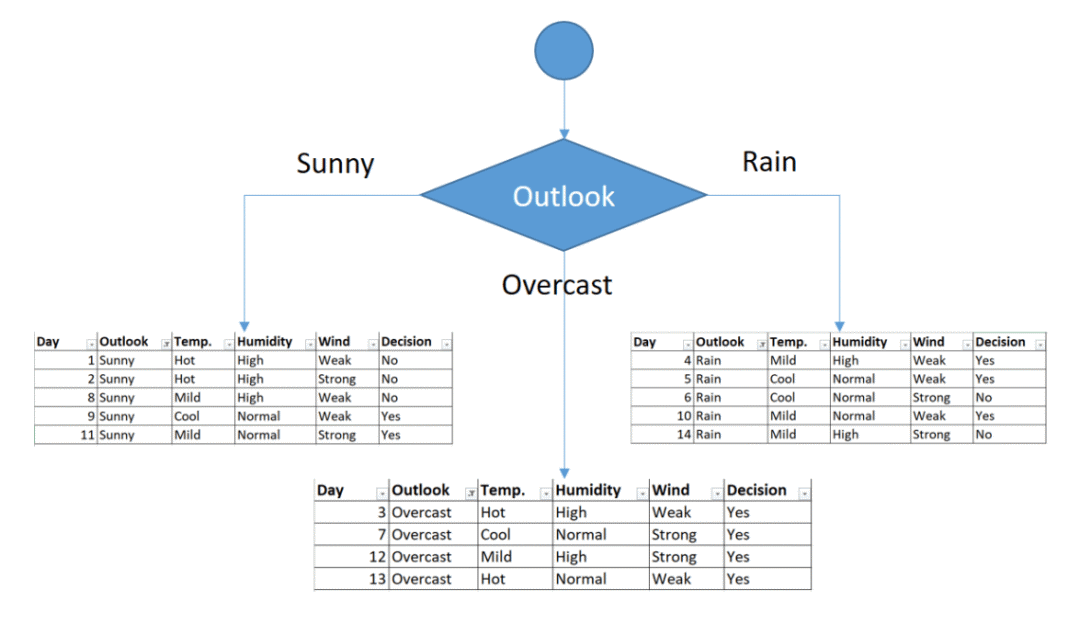
First decision would be outlook feature

You might realize that sub dataset in the overcast leaf has only yes decisions. This means that overcast leaf is over.

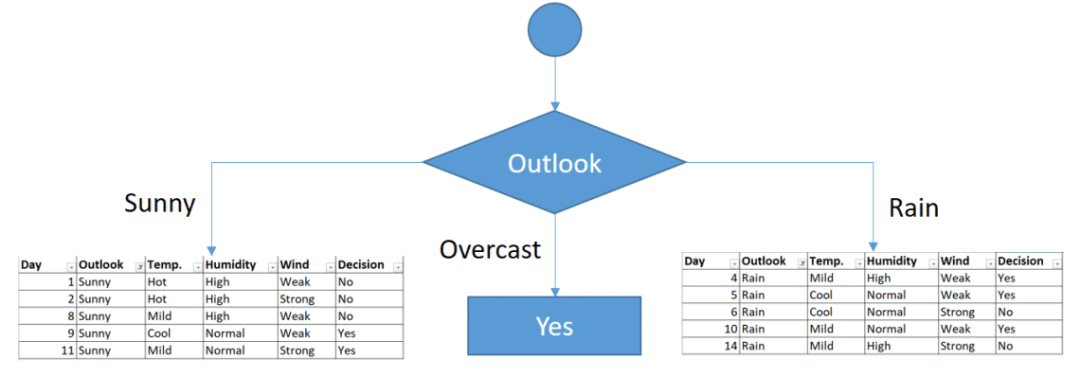
Tree is over for overcast outlook leaf

We will apply same principles to those sub datasets in the following steps.

Focus on the sub dataset for sunny outlook. We need to find the gini index scores for temperature, humidity and wind features respectively.

Day	Outlook	Temp.	Humidity	Wind	Decision
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes

Gini of temperature for sunny outlook

Temperature	Yes	No	Number of instances
Hot	0	2	2
Cool	1	0	1
Mild	1	1	2

Gini(Outlook=Sunny and Temp.=Hot) = 1 – (0/2)2 – (2/2)2 = 0

Gini(Outlook=Sunny and Temp.=Cool) = 1 – (1/1)2 – (0/1)2 = 0

Gini(Outlook=Sunny and Temp.=Mild) = 1 – (1/2)2 – (1/2)2 = 1 – 0.25 – 0.25 = 0.5

Gini(Outlook=Sunny and Temp.) = (2/5)x0 + (1/5)x0 + (2/5)x0.5 = 0.2

Gini of humidity for sunny outlook

Humidity	Yes	No	Number of instances
High	0	3	3
Normal	2	0	2

Gini(Outlook=Sunny and Humidity=High) = 1 – (0/3)2 – (3/3)2 = 0

Gini(Outlook=Sunny and Humidity=Normal) = 1 – (2/2)2 – (0/2)2 = 0

Gini(Outlook=Sunny and Humidity) = (3/5)x0 + (2/5)x0 = 0

Gini of wind for sunny outlook

Wind	Yes	No	Number of instances
Weak	1	2	3
Strong	1	1	2

Gini(Outlook=Sunny and Wind=Weak) = 1 – (1/3)2 – (2/3)2 = 0.266

Gini(Outlook=Sunny and Wind=Strong) = 1- (1/2)2 – (1/2)2 = 0.2

Gini(Outlook=Sunny and Wind) = (3/5)x0.266 + (2/5)x0.2 = 0.466

Decision for sunny outlook

We’ve calculated gini index scores for feature when outlook is sunny. The winner is humidity because it has the lowest value.

Feature	Gini index
Temperature	0.2
Humidity	0
Wind	0.466

We’ll put humidity check at the extension of sunny outlook.

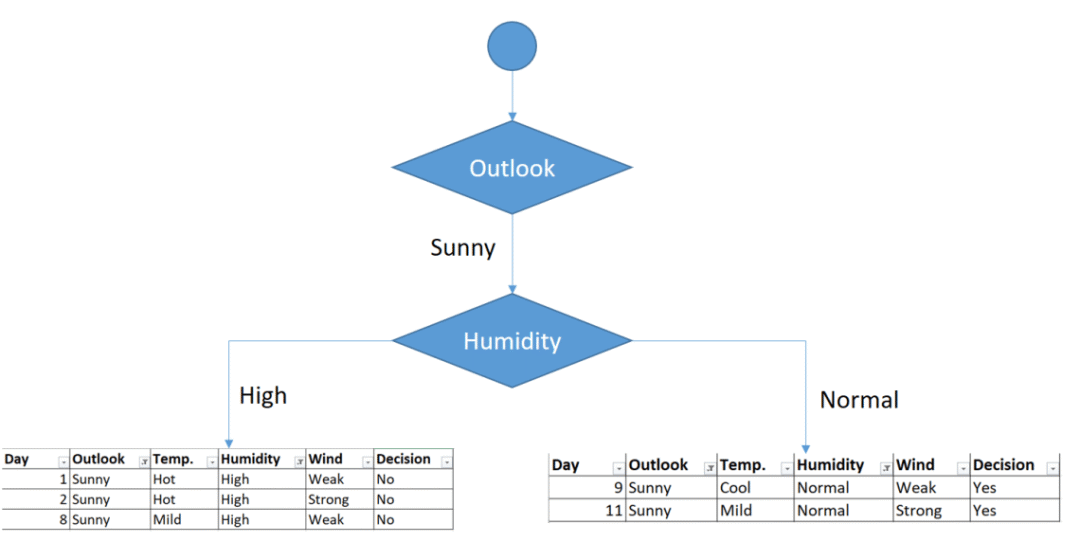
Sub datasets for high and normal humidity

As seen, decision is always no for high humidity and sunny outlook. On the other hand, decision will always be yes for normal humidity and sunny outlook. This branch is over.

Decisions for high and normal humidity

Now, we need to focus on rain outlook.

Rain outlook

Day	Outlook	Temp.	Humidity	Wind	Decision
4	Rain	Mild	High	Weak	Yes
5	Rain	Cool	Normal	Weak	Yes
6	Rain	Cool	Normal	Strong	No
10	Rain	Mild	Normal	Weak	Yes
14	Rain	Mild	High	Strong	No

We’ll calculate gini index scores for temperature, humidity and wind features when outlook is rain.

Gini of temprature for rain outlook

Temperature	Yes	No	Number of instances
Cool	1	1	2
Mild	2	1	3

Gini(Outlook=Rain and Temp.=Cool) = 1 – (1/2)2 – (1/2)2 = 0.5

Gini(Outlook=Rain and Temp.=Mild) = 1 – (2/3)2 – (1/3)2 = 0.444

Gini(Outlook=Rain and Temp.) = (2/5)x0.5 + (3/5)x0.444 = 0.466

Gini of humidity for rain outlook

Humidity	Yes	No	Number of instances
High	1	1	2
Normal	2	1	3

Gini(Outlook=Rain and Humidity=High) = 1 – (1/2)2 – (1/2)2 = 0.5

Gini(Outlook=Rain and Humidity=Normal) = 1 – (2/3)2 – (1/3)2 = 0.444

Gini(Outlook=Rain and Humidity) = (2/5)x0.5 + (3/5)x0.444 = 0.466

Gini of wind for rain outlook

Wind	Yes	No	Number of instances
Weak	3	0	3
Strong	0	2	2

Gini(Outlook=Rain and Wind=Weak) = 1 – (3/3)2 – (0/3)2 = 0

Gini(Outlook=Rain and Wind=Strong) = 1 – (0/2)2 – (2/2)2 = 0

Gini(Outlook=Rain and Wind) = (3/5)x0 + (2/5)x0 = 0

Decision for rain outlook

The winner is wind feature for rain outlook because it has the minimum gini index score in features.

Feature	Gini index
Temperature	0.466
Humidity	0.466
Wind	0

Put the wind feature for rain outlook branch and monitor the new sub data sets.

Sub data sets for weak and strong wind and rain outlook

As seen, decision is always yes when wind is weak. On the other hand, decision is always no if wind is strong. This means that this branch is over.

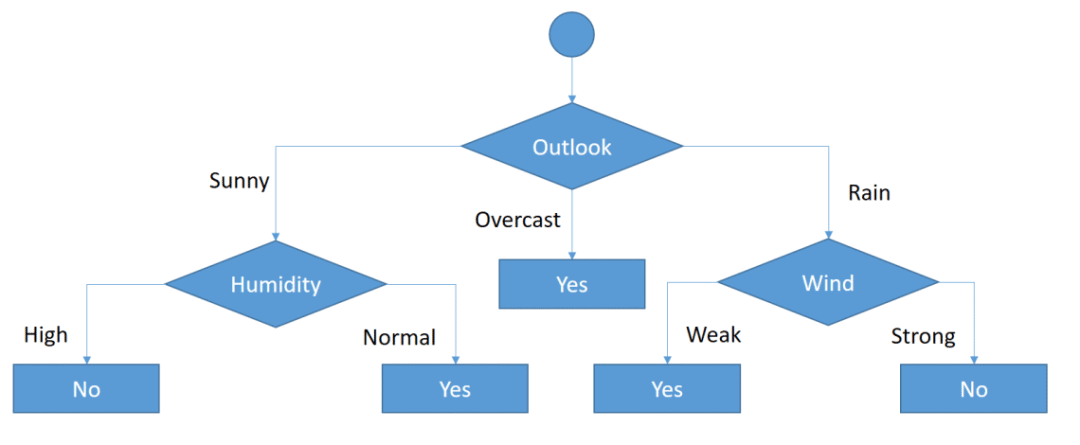
Final form of the decision tree built by CART algorithm

So, decision tree building is over. We have built a decision tree by hand. BTW, you might realize that we’ve created exactly the same tree in ID3 example. This does not mean that ID3 and CART algorithms produce same trees always. We are just lucky. Finally, I believe that CART is easier than ID3 and C4.5, isn’t it?