腾讯数据科学家手把手教你做用户行为分析(案例:出行选择)
导读:生活中的选择行为无处不在,数据分析师面对的商业场景也存在大量的用户选择问题。系统、科学地研究用户选择问题,得到选择行为背后的客观规律并基于这些规律提出业务优化策略,这些能力对于数据分析师非常重要且极具价值。

可以选择的交通方式有哪些? 同程的人多不多? 需要在什么时间到达? 出行预算是多少? 公共交通的便捷程度? 出行方式是否受天气影响?
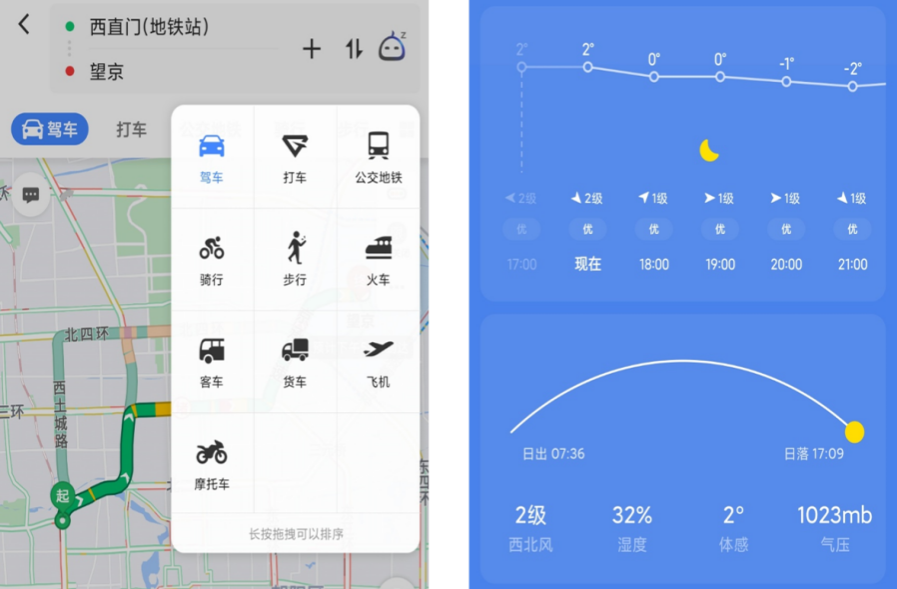
消费者在进行实际消费行为时,若从备选方案中选择了一个选项,即为首选选项,则该选项效用是最大的。 在给定的消费者预算、商品价格等因素不变的情况下,如果消费者购买了某种产品,那么他将始终做出相同的选择。
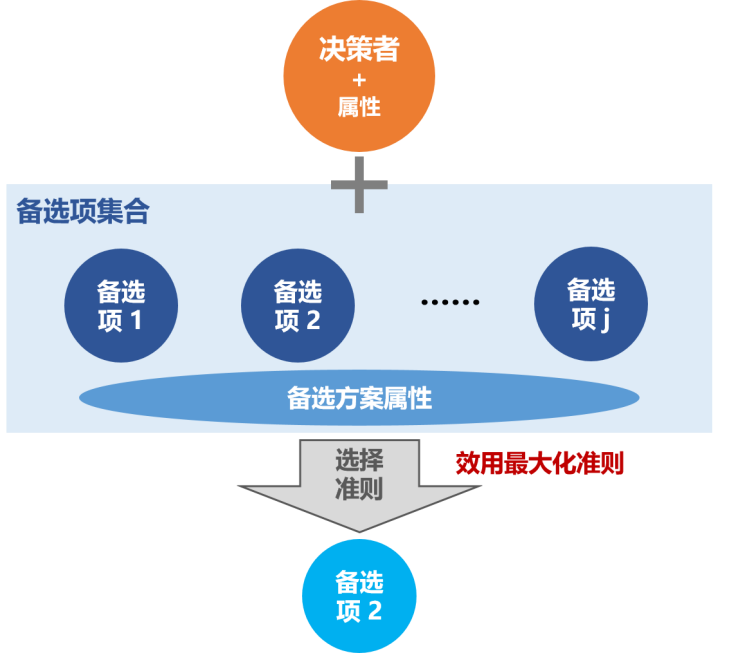
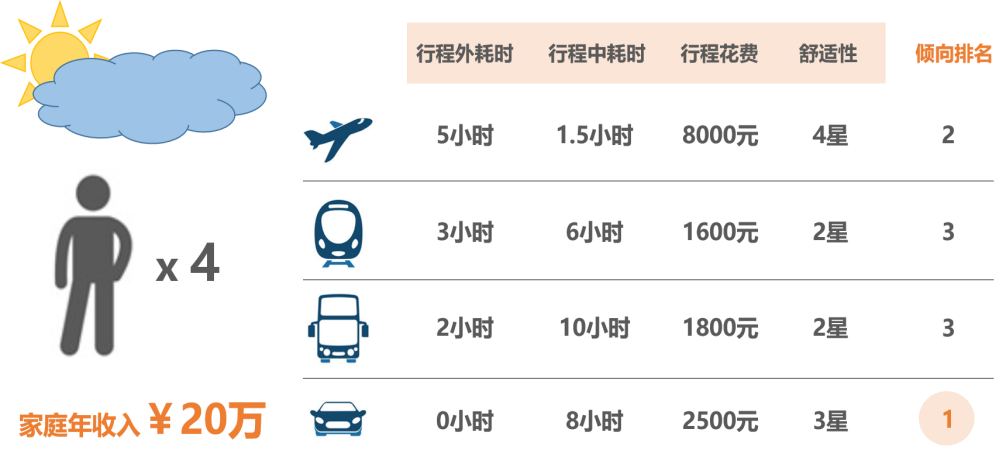
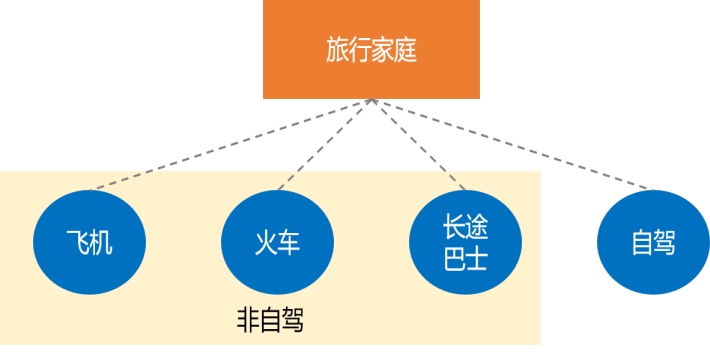
决策者:一次选择行为的主体(决策者属性包括家庭收入、出行人数、天气)。 备选项集合:飞机、火车、长途巴士、自驾车(不同决策者的备选项集合可以不同)。 备选项属性:行程外耗时、行程中耗时、行程花费、舒适性(不同备选项的属性也可以不同)。 选择准则:效用的最大化准则。 选择结果:备选项中的一个选项(每个选择过程均存在选择结果)。
OBS_ID:离散,选择行为ID HINC:连续,家庭收入 PSIZE:连续 or 离散,出行人数 TTME_AIR:连续,站点等待时间(飞机) TTME_TRAIN:连续,站点等待时间(火车) TTME_BUS:连续,站点等待时间(长途巴士) INVC_AIR:连续,金钱成本(飞机) INVC_TRAIN:连续,金钱成本(火车) INVC_BUS:连续,金钱成本(长途巴士) INVC_CAR:连续,金钱成本(自驾) INVT_AIR:连续,行程中 -时间成本(飞机) INVT_TRAIN:连续,行程中 -时间成本(火车) INVT_BUS:连续,行程中 -时间成本(长途巴士) INVT_CAR:连续,行程中 -时间成本(自驾) y:离散,是否选择自驾
代码清单1-3 软件包引入及数据读取
import numpy as np # 引入基础软件包numpy
import pandas as pd # 引入基础软件包pandas
import statsmodels.api as sm # 引入Logistic regression软件包statsmodels
from sklearn.model_selection import train_test_split # 引入训练集/测试集构造工具包
from sklearn import metrics # 引入模型评价指标AUC计算工具包
import matplotlib.pyplot as plt # 引入绘图软件包
import scipy # 引入scipy软件包完成卡方检验
# 数据读入
data_path = 'wide_data.csv'
raw_data = pd.read_table(data_path, sep=',', header=0)代码清单1-4 数据预处理
# 1. 缺失值探查&简单处理
model_data.info() # 查看每一列的数据类型和数值缺失情况
# | RangeIndex: 210 entries, 0 to 209
# | Data columns (total 9 columns):
# | ...
# | HINC 210 non-null int64
# | ...
model_data = model_data.dropna() # 缺失值处理——删除
model_data = model_data.fillna(0) # 缺失值处理——填充(零、均值、中位数、预测值等)
# 2. 数值型核查(连续变量应为int64或float数据类型)
# 若上一步中存在应为连续数值变量的字段为object,则执行下列代码,这里假设'HINC'存在为字符串'null'的值。
import re # 正则表达式工具包
float_patten = '^(-?\\d+)(\\.\\d+)?$' # 定义浮点数正则patten
float_re = re.compile(float_patten) # 编译
model_data['HINC'][model_data['HINC'].apply(lambda x : 'not_float' if float_re.match(str(x)) == None else 'float') == 'not_float'] # 查看非浮点型数据
# | 2 null
# | Name: distance, dtype: object
model_data = model_data[model_data['HINC'] != 'null']
model_data['HINC'] = model_data['HINC'].astype(float)代码清单1-5 单变量分析
# 离散变量分析
crosstab = pd.crosstab( model_data['y'],model_data['PSIZE'])
p=scipy.stats.chi2_contingency(crosstab)[1]
print("PSIZE:",p)
# PSIZE: 0.0024577358937625327
# 连续变量分析
logistic = sm.Logit(model_data['y'],model_data['INVT_CAR']).fit()
p = logistic.pvalues['INVT_CAR']
y_predict = logistic.predict(model_data['INVT_CAR'])
AUC = metrics.roc_auc_score(model_data['y'],y_predict)
result = 'INVT_CAR:'+str(p)+' AUC:'+str(AUC)
print(result)
# INVT_CAR:2.971604856310474e-09 AUC:0.6242563699629587代码清单1-6 共线性检验
from statsmodels.stats.outliers_influence import variance_inflation_factor
#共线性诊断包
X = raw_data[[ 'INVT_AIR', 'INVT_TRAIN','INVT_BUS', 'INVT_CAR']]
vif = pd.DataFrame()
vif['VIF Factor'] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
vif['features'] = X.columns
print('================多重共线性==============')
print(vif)
# | 0 14.229424 INVT_AIR
# | 1 72.782420 INVT_TRAIN
# | 2 80.279742 INVT_BUS
# | 3 35.003438 INVT_CAR
代码清单1-7 搭建LR模型
# 建模数据构造
X = model_data[[ 'HINC','PSIZE','TTME_TRAIN' , 'INVC_CAR']]
y = raw_data['y']
# 哑变量处理
dummies = pd.get_dummies(X['PSIZE'], drop_first=False)
dummies.columns = [ 'PSIZE'+'_'+str(x) for x in dummies.columns.values]
X = pd.concat([X, dummies], axis=1)
X = X.drop('PSIZE',axis=1) # 删去原离散变量
X = X.drop('PSIZE_4',axis=1) # 删去过于稀疏字段
X = X.drop('PSIZE_5',axis=1) # 删去过于稀疏字段
X = X.drop('PSIZE_6',axis=1) # 删去过于稀疏字段
X['Intercept'] = 1 # 增加截距项
# 训练集与测试集的比例为80%和20%
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size = 0.8, random_state=1234)
# 建模
logistic = sm.Logit(y_train,X_train).fit()
print(logistic.summary2())
# 重要返回信息
# | ------------------------------------------------------------------
# | Coef. Std.Err. z P>|z| [0.025 0.975]
# | ------------------------------------------------------------------
# | HINC 0.0264 0.0100 2.6477 0.0081 0.0068 0.0459
# | TTME_TRAIN 0.0389 0.0195 1.9916 0.0464 0.0006 0.0772
# | INVC_CAR -0.0512 0.0204 -2.5103 0.0121 -0.0913 -0.0112
# | PSIZE_1 -0.3077 0.7317 -0.4206 0.6741 -1.7419 1.1264
# | PSIZE_2 -1.0800 0.6417 -1.6829 0.0924 -2.3378 0.1778
# | PSIZE_3 -0.7585 0.7582 -1.0004 0.3171 -2.2444 0.7275
# | Intercept -1.8879 1.1138 -1.6951 0.0901 -4.0708 0.2950
# | =================================================================
# 模型评价
print("========训练集AUC========")
y_train_predict = logistic.predict(X_train)
print(metrics.roc_auc_score(y_train,y_train_predict))
print("========测试集AUC========")
y_test_predict = logistic.predict(X_test)
print(metrics.roc_auc_score(y_test,y_test_predict))
# | ========训练集AUC========
# | 0.7533854166666667
# | ========测试集AUC========
# | 0.6510263929618768
代码清单1-8 修正LR模型
X = X.drop('PSIZE_1',axis=1)
X = X.drop('PSIZE_2',axis=1)
X = X.drop('PSIZE_3',axis=1)
# 训练集与测试集的比例为80%和20%
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size = 0.8, random_state=1234)
# 建模
logistic = sm.Logit(y_train,X_train).fit()
print(logistic.summary2())
# 重要返回信息
# | ------------------------------------------------------------------
# | Coef. Std.Err. z P>|z| [0.025 0.975]
# | ------------------------------------------------------------------
# | HINC 0.0266 0.0096 2.7731 0.0056 0.0078 0.0454
# | TTME_TRAIN 0.0335 0.0161 2.0838 0.0372 0.0020 0.0650
# | INVC_CAR -0.0450 0.0168 -2.6805 0.0074 -0.0778 -0.0121
# | Intercept -2.3486 0.8275 -2.8384 0.0045 -3.9704 -0.7269
# | =================================================================
print("========训练集AUC========")
y_train_predict = logistic.predict(X_train)
print(metrics.roc_auc_score(y_train,y_train_predict))
print("========测试集AUC========")
y_test_predict = logistic.predict(X_test)
print(metrics.roc_auc_score(y_test,y_test_predict))
# | ========训练集AUC========
# | 0.7344618055555555
# | ========测试集AUC========
# | 0.7419354838709677连续变量:odd(xi+1)/odd(xi)-1=exp(βi)-1 离散变量:odd(xj=1)/odd(xj=0)-1=exp(βj)-1

评论
