阿⾥达摩院最新FEDformer,⻓程时序预测全⾯超越SOTA|ICML 2022
新智元报道

新智元报道
编辑:好困 LRS
【新智元导读】阿里巴巴达摩院最近发布了一个新模型FEDformer模型,不光计算复杂度降为线性,预测精度还比SOTA高22.6%


分析
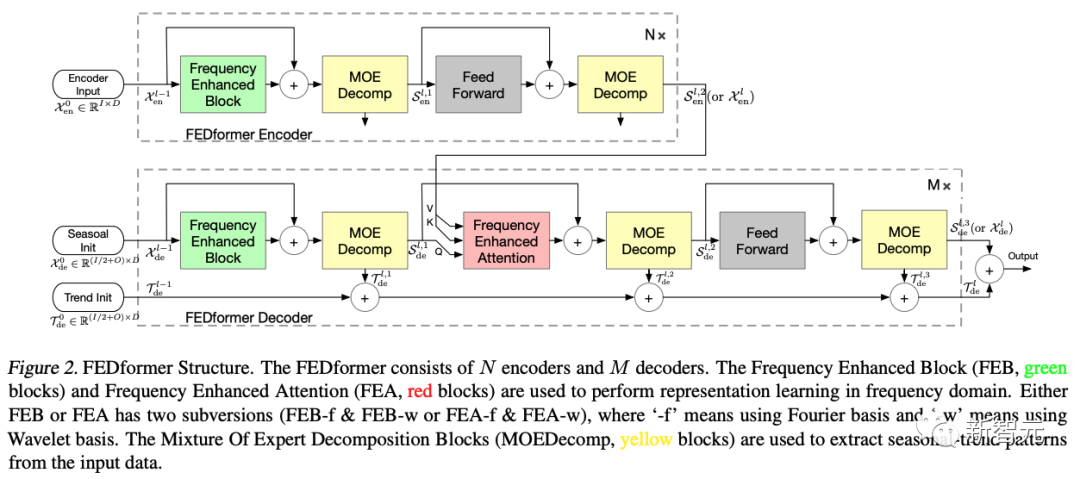
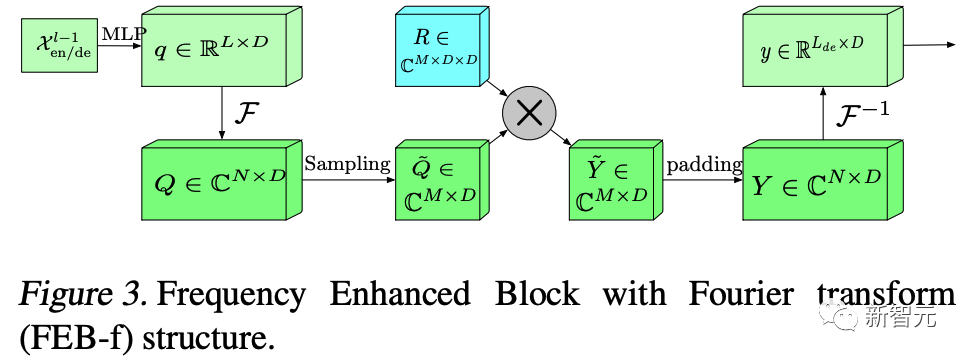
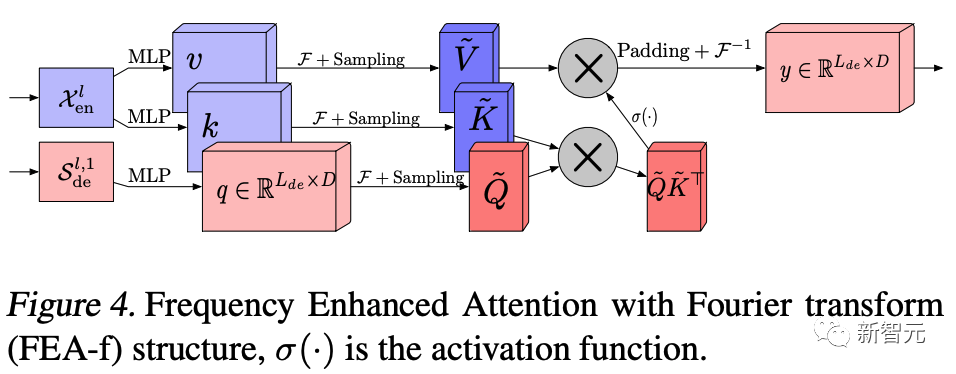
首先将原始时域上的输入序列投影到频域。
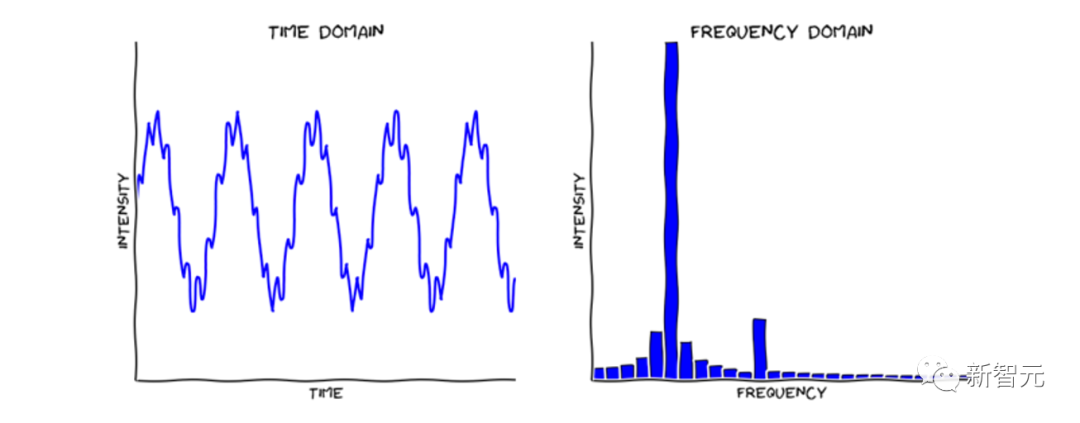
再在频域上进行随机采样。这样做的好处在于极大地降低了输入向量的长度进而降低了计算复杂度,然而这种采样对输入的信息一定是有损的。但实验证明,这种损失对最终的精度影响不大。因为一般信号在频域上相对时域更加「稀疏」。且在高频部分的大量信息是所谓「噪音」,这些「噪音」在时间序列预测问题上往往是可以舍弃的,因为「噪音」往往代表随机产生的部分因而无法预测。相比之下,在图像领域,高频部分的“噪音”可能代表的是图片细节反而不能忽略。
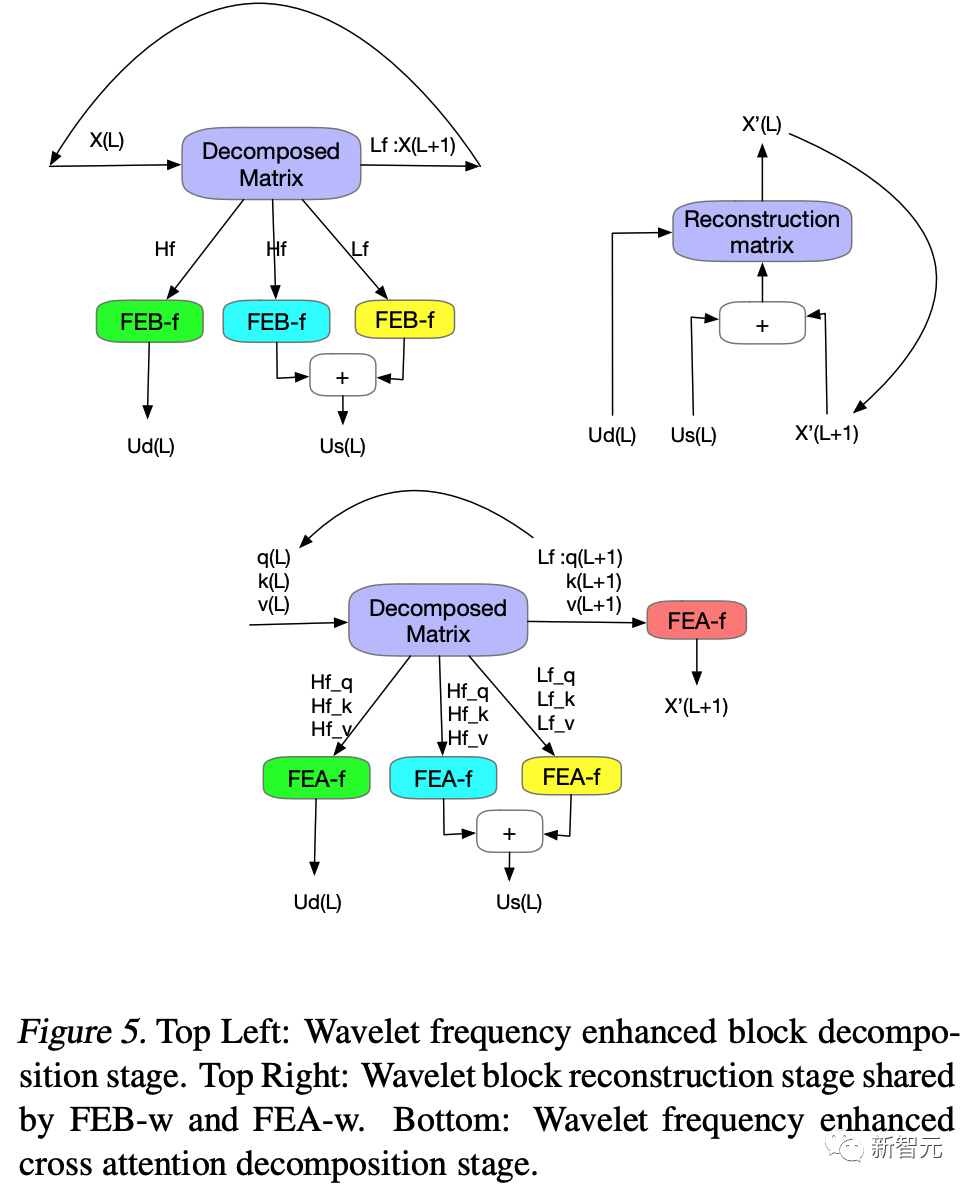
在学习阶段,FEB 采用一个全联接层 R 作为可学习的参数。而 FEA 则将来自编码器和解码器的信号进行cross-attention操作,以达到将两部分信号的内在关系进行学习的目的。
频域补全过程与第2步频域采样相对,为了使得信号能够还原回原始的长度,需要对第2步采样未被采到的频率点补零。
投影回时域,因为第4步的补全操作,投影回频域的信号和之前的输入信号维度完全一致。
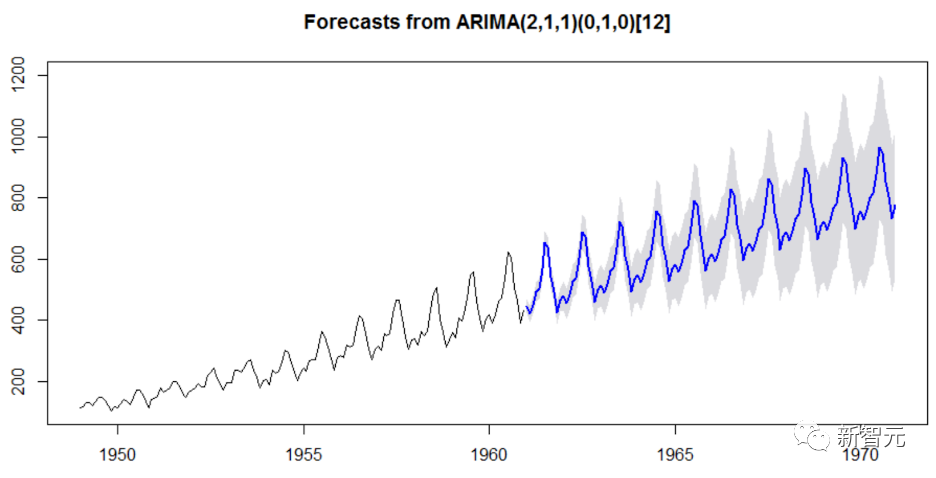
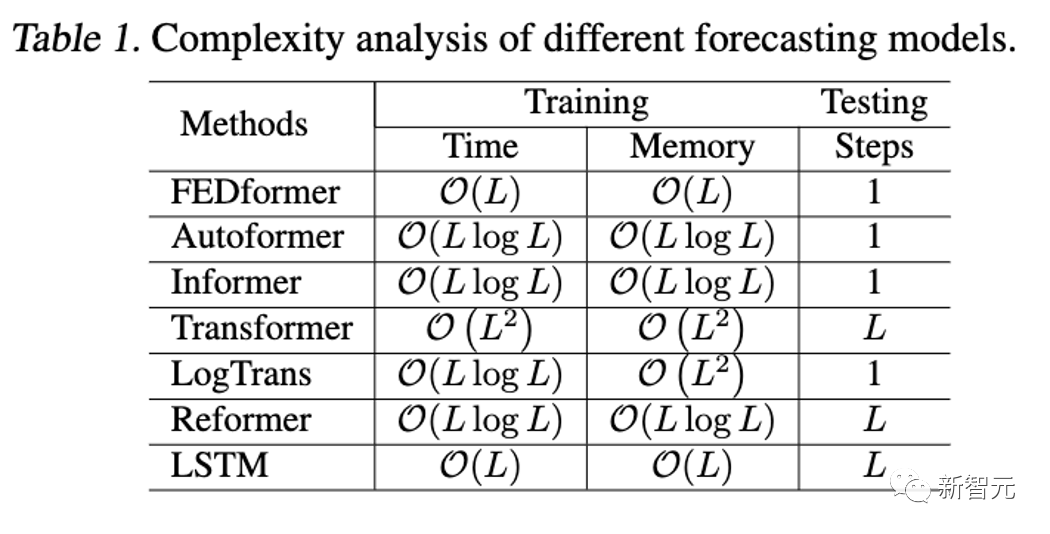
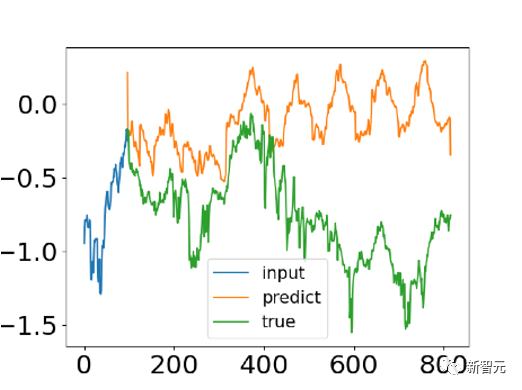
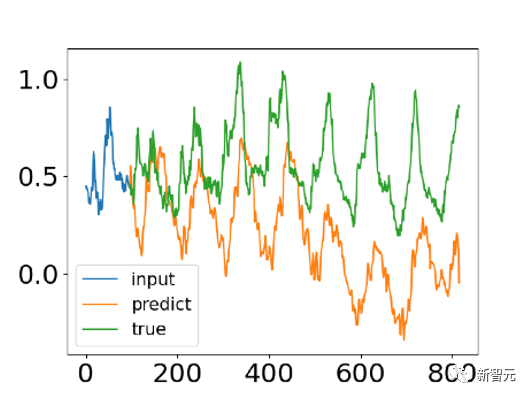
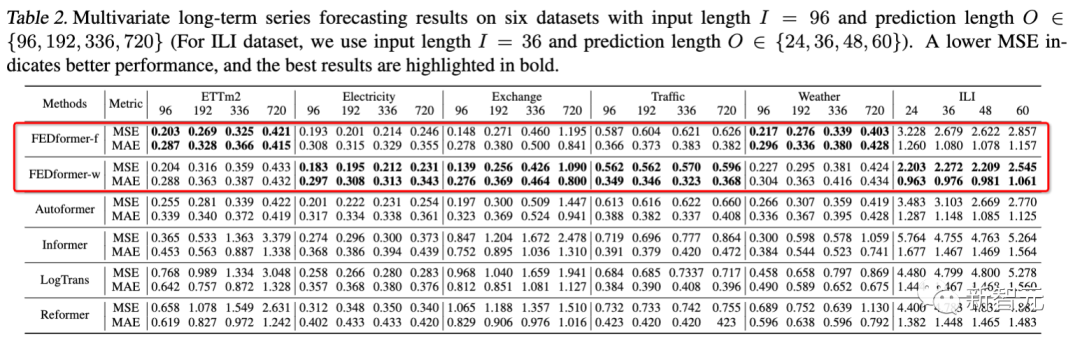
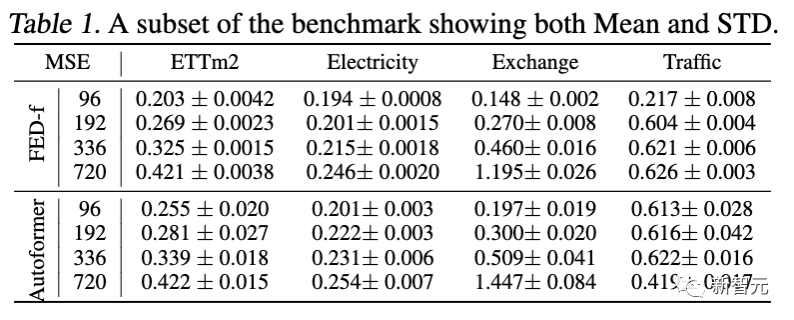
实验
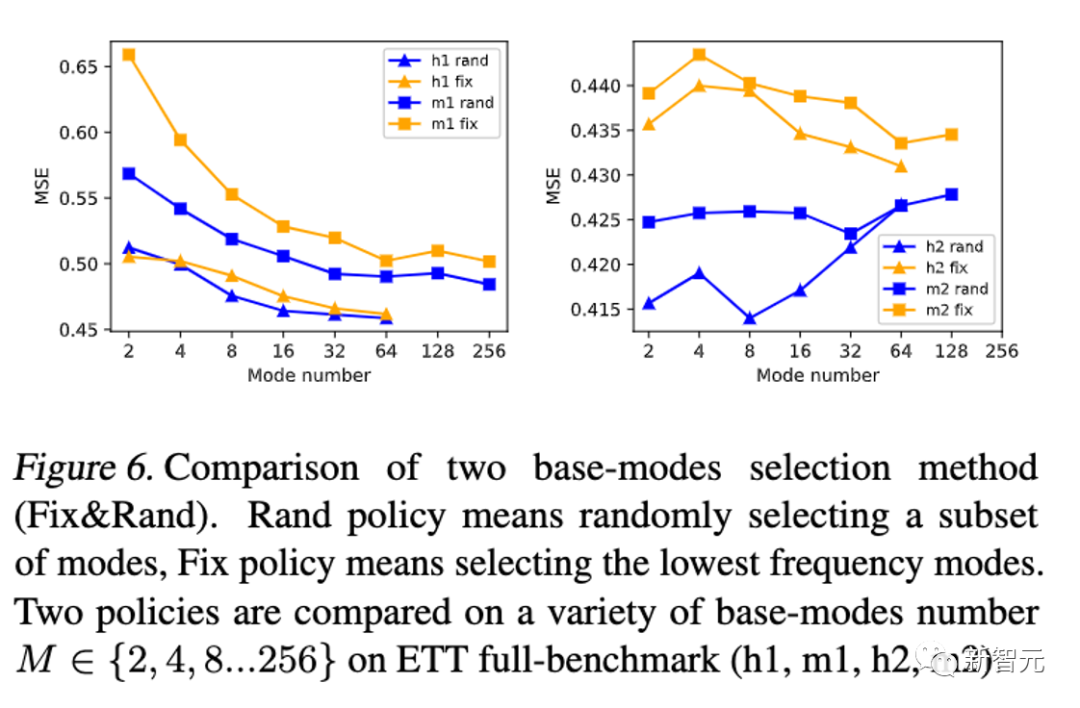
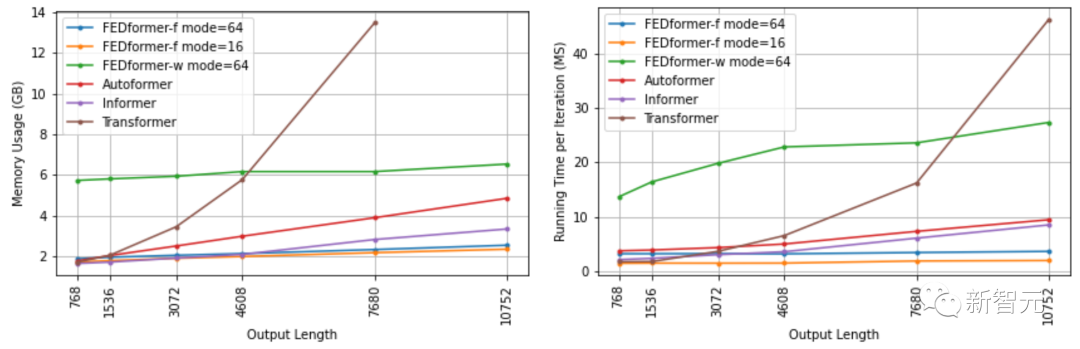
总结
延伸阅读(近期工作):

评论
